МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ ПРИРОДЫ, ОБЩЕСТВА И

ЧЕЛОВЕКА «ДУБНА»

Кафедра энергии и окружающей среды

Э.М. Абадеев

Методические указания

к решению контрольных задач

по теоретической механике.

Учебно-методическое пособие

Дубна

2011г.

Контрольные работы по теоретической механике охватывают три основных раздела этой дисциплины – статику, кинематику и динамику. Каждая контрольная работа выполняется и сдается на проверку отдельно в сроки, предусмотренные учебным графиком, в соответствии с индивидуальным номером варианта, заданного студенту. Задачи контрольных работ приведены в методическом сборнике, имеющемся на кафедре в печатном и электронном видах. Выполнение работ с использованием компьютерных технологий приветствуется.

Раздел 1. Статика.

В разделе статики студентам предлагаются для решения три типовые задачи:

- задача С-1 - на разложение заданной силы по заданным направлениям на плоскости;

- задача С-2 – на определение реакций опор составной балки, нагруженной произвольной системой сил на плоскости;

- задача С-3 - на определение реакций опор твердого тела, нагруженного произвольной системой сил в пространстве.

Задача С-1.

К кронштейну с стержнями 1 и 2, веса которых не учитываются, приложена сила Р=15кН. Найти усилия в стержнях F₁ и F₂. Углы, обозначенные на схеме, имеют величины: =24°, =39°, =23°.

Решение.

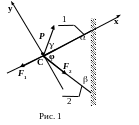
Задача может быть решена несколькими способами. Рассмотрим три из них.

1. Мысленно вырежем т. С и рассмотрим ее равновесие под действием заданной и искомых сил. Аналитические условия равновесия т. С под действием пучка сил (Р, F₁, F₂) в проекциях на оси х, у записываются:

ΣХ = 0; Pcos-F₁+F₂cos φ = 0;

ΣY = 0; Psin-F₂sin φ = 0. (1)

Следует обратить внимание на выбор системы координатных осей х, у. На рис.1 они выбраны таким образом, чтобы одна из осей прошла бы вдоль одного из стержней. В таком случае в системе (1) одно из уравнений непосредственно дает величину одной из двух неизвестных, после чего из второго уравнения находится вторая искомая величина.

О чевидно, φ =180° - (+ ) = 119°. Подстановка всех данных в систему (1) дает:

15cos23°-F₁+F₂cos119° = 0,

15sin23°-F₂sin119° = 0,

откуда F₂ = [кН];

F₁= 15*0,9205 – 6,70*0,4848=10,56 [кН].

2. Для следующих двух способов решения задачи, связанных с геометрическими построениями, необходимо схему кронштейна представлять не произвольно, как на рис. 1, а изображать в соответствии с заданными величинами углов , ,  (Рис. 2).

Геометрическое условие равновесия т. С под действием пучка сил (Р, F₁, F₂) состоит в требовании замкнутости силового треугольника, построенного на векторах этих сил.

Поэтому второй способ решения задачи может состоять, например, в применении теоремы синусов к треугольнику АВС. Предварительно определим угол δ = 180° - φ – γ =180° – 119° – 23° = 38°. Далее запишем соотношения теоремы синусов:

;

.

Третий способ состоит в том, чтобы на рис. 2 определить масштаб сил по известной величине Р и определить искомые силы по замерам с рис. 2 и вычисленному масштабу. По рис. 2 масштаб определяется:

В таком случае

Полученные этим способом результаты могут считаться достаточно точными для графо-аналитического метода.

Задача С-2.

Найти реакции в опорах А, В, С и шарнире D сочлененной балки (рис. 1). Заданные величины: Р₁ = 3кН, Р₂ = 5кН, q = 9кН/м, m = 0,5кНм,  = 60°, a = 0,4м, b = 0,5м, c = 0,3м, d = 0,2м, e = 0,3м, l = 1,2м.

Решение.

Прежде всего, доопределим недостающий размер f = l - c - d - e = 0,4м.

Д алее, в соответствии с условными обозначениями опор, изобразим искомые реакции опор А, В, С и шарнира D. При этом разделим сочлененную балку по шарниру D на левую АD и правую DА части (рис. 2). Выберем оси координат (ху), в которой будем составлять системы уравнений статического равновесия.

Изображенные на рис. 2 реакции шарнира D для левой и правой частей балки, в соответствии с аксиомой статики о силах взаимодействия двух тел, попарно равны по величине и противоположны по направлению: R_Dx = -R´_Dx, R_Dy = - R´_Dy.

С учетом сказанного в задаче всего 6 неизвестных: R_А, R_Вx, R_Ву, R_С, R_Dx, R_Dу. Таким образом, задача имеет единственное решение, т.к. для двух твердых тел на плоскости можно составить именно 6 уравнений равновесия:

Для левой балки –

ΣF_ix = 0; P₁cosα + R_Dx = 0;

ΣF_iу = 0; R_А - P₁sinα –q(b-a) + R_Dy = 0;

ΣM_D = 0; -R_Аb + P₁sinα(b-a) + q(b-a)²/2 = 0.

Для правой балки –

ΣF_ix = 0; - R_Dx + R_Bx = 0;

ΣF_iy = 0; - R_Dy – qc + R_By + P₂ + R_C = 0;

ΣM_B = 0; R_Dy(c+f) + qc(c/2+f) – m – P₂d + R_C(d+e) = 0.

При составлении уравнения моментов за точку приведения следует выбирать точку одной из опор, реакция которой неизвестна (для левой балки это т.А или т.D, для правой балки т.В или т.С; реакция R_Dy будет вычислена ранее).

Таким образом, получаем систему уравнений, разрешаемую в следующем порядке.

1. P₁cosα + R_Dx = 0; R_Dx = - P₁cosα; R_Dx = -3cos60° = -1,5кН.

2. -R_Dx + R_Bx = 0; R_Bx = R_Dx; R_Bx = -1,5кН.

3. -R_Аb + P₁sinα(b-a) + q(b-a)²/2 = 0; R_А = [P₁sinα(b-a) + q(b-a)²/2]/b; R_А = [3sin60°(0,5-0,4) + 9(0,1)²/2]/0,5; R_А = 0,6096кН.

4. R_А - P₁sinα –q(b-a) + R_Dy = 0; R_Dy = P₁sinα + q(b-a) - R_А = 3sin60° + 9(0,5-0,4) – 0,6096; R_Dy = 2,888кН.

5. R_Dy(c+f) + qc(c/2+f) – m – P₂d + R_C(d+e) = 0; R_C = [ - R_Dy(c+f) - qc(c/2+f) + m + P₂d]/(d+e) = [-2,888(0,3 + 0,4) - 9×0,3(0,15+0,4) + 0,5 + 5×0,2]/(0,2 + 0,3);

R_C = - 4,013кН.

6. - R_Dy – qc + R_By - P₂ + R_C = 0; R_By = R_Dy + qc + P₂ - R_C = 2,888+ 9×0,3 + 5 + 4,013;

R_By = 14,60кН.

Проверка правильности вычислений для каждой балки возможна путем составления уравнения моментов для другой точки приведения.

Для левой балки

ΣM_А = 0; - P₁sinα×a - q(b-a)(a + (b - a)/2) + R_Dyb = 0;

- 3sin60°×0,4 – 9(0,5 – 0,4)(0,4 + 0,1/2) + 2,888×0,5 = 0; 1,444 – 1,444 = 0.

Для правой балки

ΣM_С = 0; P₂×e - R_By(d + e) – m + qc(l – c/2) + R_Dyl = 0;

5×0,3 – 14,60(0,2 + 0,3) -0,5 + 9×0,3(1,2 – 0,3/2) + 2,888×1,2 = 0; 7,8 –7,8 = 0.

Задача С-3.

Однородная плита длиной а = 0,4м и шириной b = 0,3м имеет вес Р =1,5кН. Плита, закрепленная с помощью сферического шарнира В, цилиндрической петли А и стержня СЕ, наклоненного к плоскости плиты под углом  = 60°, нагружена силой F = 3кН, равномерно распределенной нагрузкой q = 6кН/м и парой сил с моментом m = 0,2кНм (рис.1). Определить реакции шарнира, петли и наклонного стержня.

Решение.

Изобразим искомые реакции опор А, В, С в соответствии с условными обозначениями опор. Цилиндрический шарнир (петля) А имеет две составляющие пространственной реакции, сферический шарнир В – три составляющие, а реакция стержня СЕ в точке С может направлена только вдоль оси стержня (рис.1).

Таким образом, в задаче 6 неизвестных: R_Аx, R_Аz, R_Вx, R_Ву, R_Bz, R_С; задача имеет единственное решение, т.к. для твердого тела в трехмерном пространстве можно составить именно 6 уравнений равновесия:

1. ΣF_ix = 0; R_Аx + R_Вx - R_Сcosα = 0;

2. ΣF_iу = 0; R_Ву = 0;

3. ΣF_iz = 0; R_Аz + R_Bz - R_Сsinα – P – F - qa = 0.

4. ΣM_x = 0; (R_Bz – R_Csinα)a –Pa/2 – qa²/2 = 0;

5. ΣM_y = 0; (R_Csinα + F)b + Pb/2 + qab = 0;

6. ΣM_z = 0; - R_Вxa + m + R_C cosα a = 0.

Система решается в следующем порядке.

1. R_Ву = 0.

2. Из пятого уравнения находим R_С = -(F + P/2 + qa)/ sinα; R_С = - (3 + 1,5 + 6×0,4)/sin60°. R_С = - 7,967кН. Знак – означает, что на самом деле реакция в стержне СЕ направлена в противоположную сторону.

3. Из шестого уравнения определяем R_Вx = (m/a + R_C cosα); R_Вx = (0,2/0,4 - 7,967 cos60°). R_Bx = - 7,37335кН. Эта реакция также направлена в сторону, противоположную изображенной на рис 1.

4. Из первого уравнения находим R_Аx = R_Сcosα - R_Вx; R_Аx = -7,967 cos60° + 7,37335. R_Аx = 3,38985кН.

5. Из четвертого уравнения определяем R_Вz = R_Csinα + P/2 + qa/2; R_Вz = - 7,967 sin60° + 1,5/2 + 6×0,4/2; R_Bz = - 4,950кН. Реакция также направлена в противоположную сторону по отношению к изображенной на рис 1.

6. Из третьего уравнения находим R_Аz = - R_Bz + R_Сsinα + P + F + qa; R_Аz = 4,950 + 7,967 sin60° +1,5 + 3 + 6×0,4. R_Аz = 18,75кН.

Окончательно величины реакций в опорах А и В находятся:

R _А = √(R_Аx² + R_Аz² _); R_А = 19,05кН. R_B = √(R_Bx² + R_Bz² _); R_B = 8,881кН.