3.4. Определение напряжений в стенке тонкостенного сосуда

Ц е л ь р а б о т ы: определение напряжений в стенке тонкостенного осесимметричного сосуда, находящегося под действием внутреннего давления, и сравнивание с напряжениями, полученными расчетным путем.

Т е о р е т и ч е с к а я ч а с т ь р а б о т ы. Тонкостенным осесимметричным сосудом называют оболочку, срединная поверхность которой представляет собой поверхность вращения, а соотношение толщины её стенки и наименьшего главного радиуса кривизны срединной поверхности составляет .

Срединная поверхность - геометрическое место точек, равноотстоящих от обеих поверхностей оболочки.

В стенке тонкостенного осесимметричного сосуда толщиной , находящегося под внутренним давлением, напряжения определяют по известной формуле Лапласа (рис. 3.12):

. (3.26)

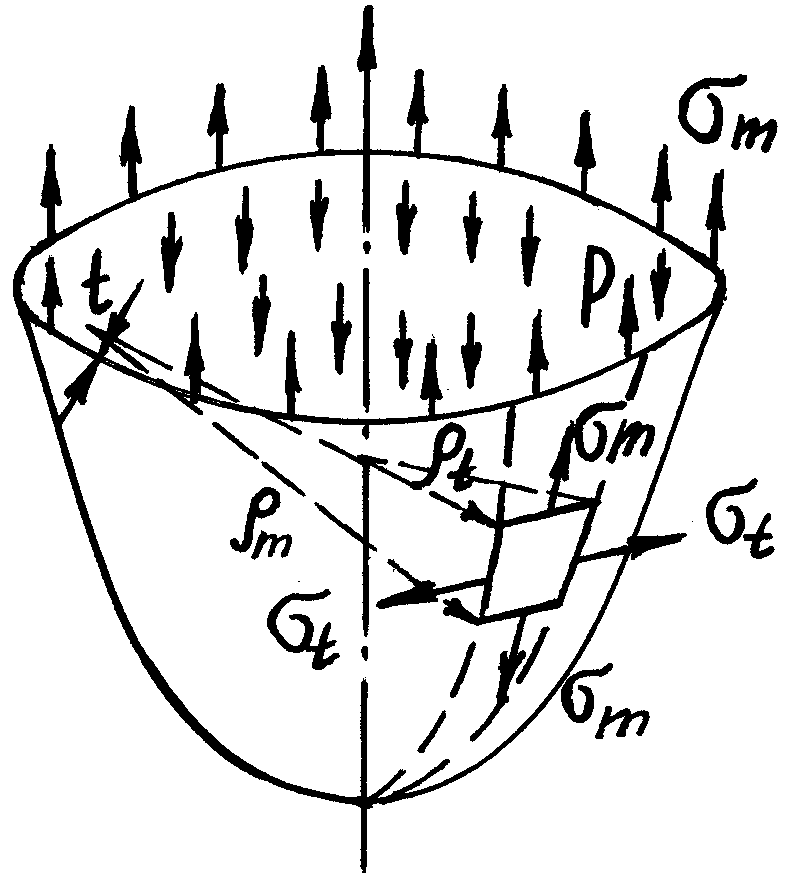
Рис. 3.12. Тонкостенный осесимметричный сосуд

В настоящей работе используют тонкостенный цилиндрический сосуд (рис. 3.13,а).

В этом случае принимают , а (радиус кривизны образующей цилиндра). Из уравнения Лапласа (3.23) получают для окружного напряжения

.

Откуда

. (3.27)

Меридиональное напряжение определяют из условия равновесия отсеченной части сосуда (рис. 3.13,б) по формуле

. (3.28)

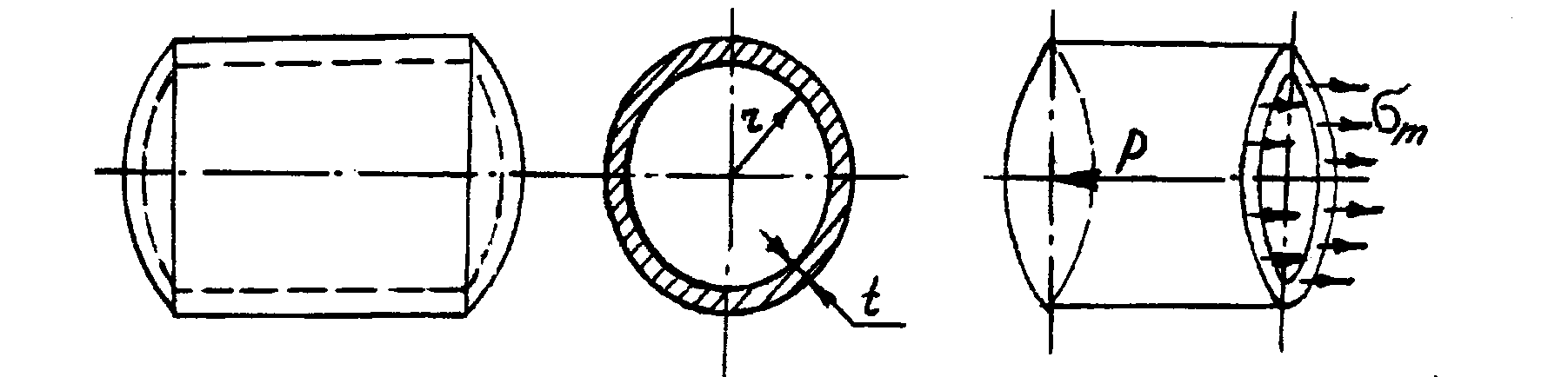
а) б)

Рис. 3.13. Тонкостенный цилиндрический сосуд

Сравнивая и в цилиндрическом сосуде, видим что

. (3.29)

О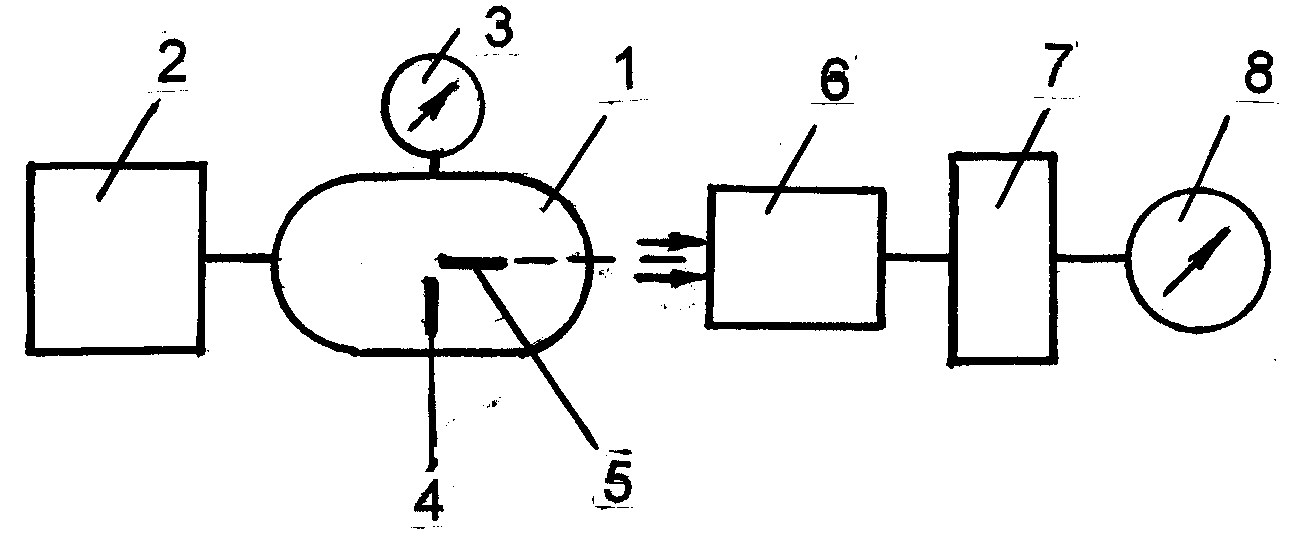 п и с а н и е л а б о р а т о р н о й у с т а н о в к и. Схема установки показана на рис. 3.14 и представляет собой тонкостенный цилиндрический сосуд 1, в который из источника давления 2 подается газ.

Рис. 3.14. Схема лабораторной установки

Контроль за величиной давления осуществляется по манометру 3. На поверхности сосуда в средней его части наклеены тензодатчики в окружном 4 и меридиональном 5 направлениях, которые подключены к тензоусилителю 6. Через коммутатор 7 сигнал с тензодатчиков после усиления подается на измерительный прибор 8 (методику тензоизмерений см. в работе 3.1).

М е т о д и к а п р о в е д е н и я о п ы т а и о б р а б о т к а

р е з у л ь т а т о в. 1. Задают исходные данные: окружной радиус кривизны меридиональный радиус кривизны толщину стенки осесимметричной оболочки ; ступень внутреннего давления .

2. Балансируют мостовые схемы тензоусилителя, предварительно включенного в сеть для прогрева в течение не менее 20 минут.

3. Подают внутреннее давление Р, снимают показания и на измерительном приборе 8 тензоусилителя каждого тензодатчика и записывают в журнал наблюдений. Опыт повторяют 2 – 3 раза, увеличивая давление равными ступенями и записывая для каждого опыта результаты испытаний в журнал наблюдений. По результатам измерений вычисляют приращения показаний тензодатчиков и на заданную ступень давления , а затем определяют среднее значение этих приращений и .

4.Вычисляют опытные значения окружного и меридионального напряжения при заданной ступени давления по формулам:

; (3.30)

где и - тарировочные коэффициенты тензодатчиков.

5. Вычисляют теоретические значения напряжений и при той же ступени давления по формулам (3.27) и (3.28) и проводят сопоставление полученных результатов. При этом обрабатывают результаты опытов согласно требованиям раздела 4.

Содержание отчета

1. Название лабораторной работы.

2. Цель работы.

3. Схема лабораторной установки.

4. Исходные данные.

   1. Окружной радиус кривизны .

   2. Меридиональный радиус кривизны .

   3. Толщина стенки сосуда .

5. Теоретические расчеты.

   1. Окружное напряжение .

   2. Меридиональное напряжение .

6. Результаты опыта.

№ п/п	Давление	Ступень внутреннего давления	Показания тензодатчиков		Приращения показаний тензодатчиков
Средние значения приращений

7. Обработка результатов опыта.

   1. Значение окружного напряжения .

   2. Значение меридионального напряжения .

8. Сравнение опытных и теоретических значений.

Вопросы для самоконтроля

1. Какова цель лабораторной работы?

2. Как устроена лабораторная установка?

3. Какие тензодатчики применяют в работе? Опишите их устройство.

4. Что называют тонкостенной осесимметричной оболочкой?

5. Что называют срединной поверхностью оболочки (сосуда)?

6. Как записывают уравнение Лапласа?

7. Какое соотношение существует между меридиональным и окружным напряжениями в цилиндрической тонкостенной оболочке?

8. Что означают символы: ?

9. Как теоретически вычислить меридиональные и окружные напряжения в стенке цилиндрического сосуда?

10. Какова методика опытного определения этих напряжений?

Литература: [5] - §§ 64, 65; [7] - §§ 82.