1.2.2.Системы счисления
В двоичной системе счисления для обозначения чисел используют цифры «1» и «0».
Чтобы двоичное число перевести в десятичное необходимо записать сумму степеней 2n, соответствующих тем разрядам двоичного числа, в которых записаны «1».
1011102 = 1 * 25 + 0 * 24 + 1 * 23 + 1 * 22 + 1 * 21 + 0 * 20 =3610
Чтобы десятичное число перевести в 2 необходимо выполнить ряд последовательных делений числа на 2 до тех пор, пока частное не станет <2 затем частное и остатки записать в обратном порядке.
2210 = 101102
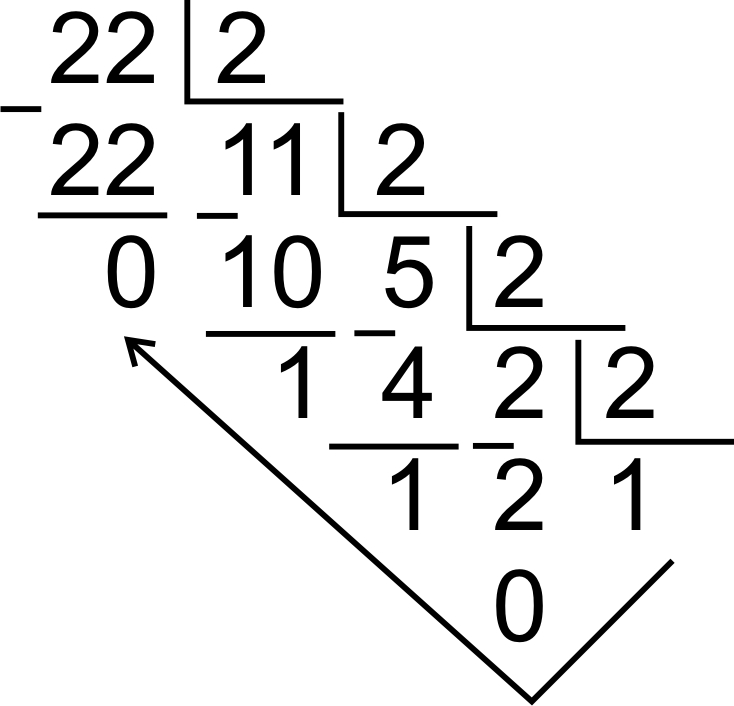
Чтобы двоичное число перевести в 8 необходимо его разделить на группы по 3 разряда (справа налево) и каждую группу записать в виде восьмеричной цифры.
1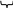
01
0112 =
538;
Чтобы двоичное число перевести в 16 необходимо его разделить на группы по 4 разряда (справа налево) и каждую группу записать в виде шестнадцатиричной цифры или буквы
10 10112
= 2B16
В восьмеричной системе счисления для обозначения чисел используют цифры «0», «1» «2», «3», «4», «5», «6», «7».
Чтобы восьмеричное число перевести в десятичное, необходимо записать сумму произведений 8n на соответствующие коэффициенты.
1358=1*82+3*81+5*80=64+24+5=9310
Чтобы десятичное число перевести в 8 необходимо выполнить ряд последовательных делений числа на 8 (нацело) до тех пор, пока частное не станет <8 затем частное и остатки записать в обратном порядке.
12010=1688
Чтобы восьмеричное число перевести в двоичное, необходимо каждую цифру восьмеричного числа записать в виде трехразрядного двоичного кода.
2378= 100111112
В шестнадцатиричной системе счисления для обозначения чисел используют цифры «0», «1» «2», «3», «4», «5», «6», «7», «8», «9» и буквы «A», «B», «C», «D», «E», «F».
Чтобы шестнадцатиричное число перевести в десятичное, необходимо записать сумму произведений 16n на соответствующие коэффициенты.
25F16=2*162+5*161+15*160= 512+80+15=60710
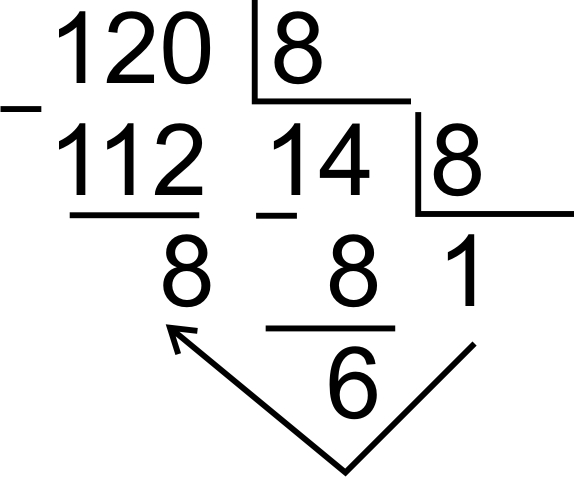
Чтобы десятичное число перевести в 16 необходимо выполнить ряд последовательных делений числа на 16 (нацело) до тех пор, пока частное не станет <16 затем частное и остатки записать в обратном порядке.
50010 = 1 F 416
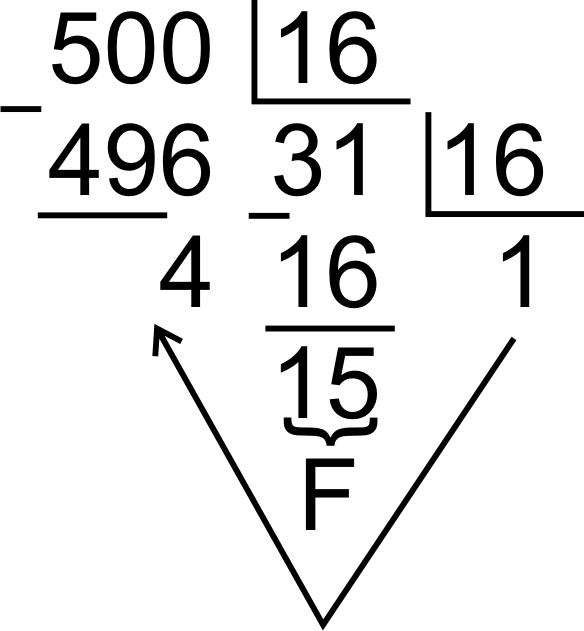
Чтобы шестнадцатиричное число перевести в двоичное, необходимо каждую цифру и букву шестнадцатиричного числа записать в виде четырехразрядного двоичного кода.
AB816=1010101110002
1.2.3. Правила двоичной арифметики
Сложение в двоичной системе
счисления выполняется также как и в
десятичной системе счисления, но единица
переноса в старший разряд возникает в
том случае, если сумма разрядов слагаемых
2.
Вычитание в двоичной системе счисления заменяется алгебраическим сложением положительного и отрицательного числа. В этом случае используется обратный или дополнительный код.
Чтобы выполнить вычитание с использованием обратного кода необходимо:
– вычитаемое перевести в обратный код (цифры всех разрядов, кроме знакового, проинвертировать);
– сложить с уменьшаемым (складывать все разряды);
– если возникает единица переноса из знакового разряда, то она прибавляется к младшему разряду суммы;
– если в результате получим отрицательное число, то оно представлено в обратном коде и его необходимо перевести в прямой код.
Чтобы выполнить вычитание с использованием дополнительного кода необходимо:
– вычитаемое перевести дополнительный код (цифры всех разрядов, кроме знакового, проинвертировать и к младшему разряду добавить единицу);
– сложить с уменьшаемым (складывать все разряды);
– если возникает единица переноса из знакового разряда, то она отбрасывается;
– если в результате получим
отрицательное число, то оно представлено
в дополниткльном коде и его необходимо
перевести в прямой код 
(вычесть
единицу и цифры всех разрядов, кроме
знакового, проинвертировать).
С использованием обратного кода (таблица 1.2.3.1.)
98 – 83
Таблица 1.2.3.1.
А |
= |
98 |
|
= |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
В |
= |
-83 |
|
= |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Вобр |
|
= |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
А |
|
= |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
|
|
|
= |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
|
|
|
+ |
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
|
10 |
|
= |
15 |
|
|
|
|
|
|
|
83 – 98
А |
= |
83 |
|
= |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|||||||||
В |
= |
-98 |
|
= |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
||||||||
|
|
Вобр |
|
= |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
А |
|
= |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
|
обр |
|
= |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
2 |
|
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
|
10 |
|
= |
-15 |
|
|
|
|
|
|
|
С использованием дополнительного кода (таблица 1.2.3.2.)
98 – 83
Таблица 1.2.3.2.
А |
= |
98 |
|
= |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
В |
= |
-83 |
|
= |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
|
Вобр |
|
= |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
+ |
|
|
|
|
|
|
|
1 |
|
|
Вдоп |
|
= |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
А |
|
= |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
|
|
|
= |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
|
2 |
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
|
10 |
|
= |
15 |
|
|
|
|
|
|
|
83 – 98
А |
= |
83 |
|
= |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
В |
= |
-98 |
|
= |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
|
Вобр |
|
= |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
|
|
|
+ |
|
|
|
|
|
|
|
1 |
|
|
Вдоп |
|
= |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
А |
|
= |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
|
доп |
|
= |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
|
|
|
– |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
2 |
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
|
10 |
|
= |
-15 |
|
|
|
|
|
|
|