Gray-scale Background

Before discussing advancements in gray-scale technology developed as part of this dissertation, the theoretical framework and design limitations for the chosen grayscale implementation must be discussed.

1. Theoretical Background

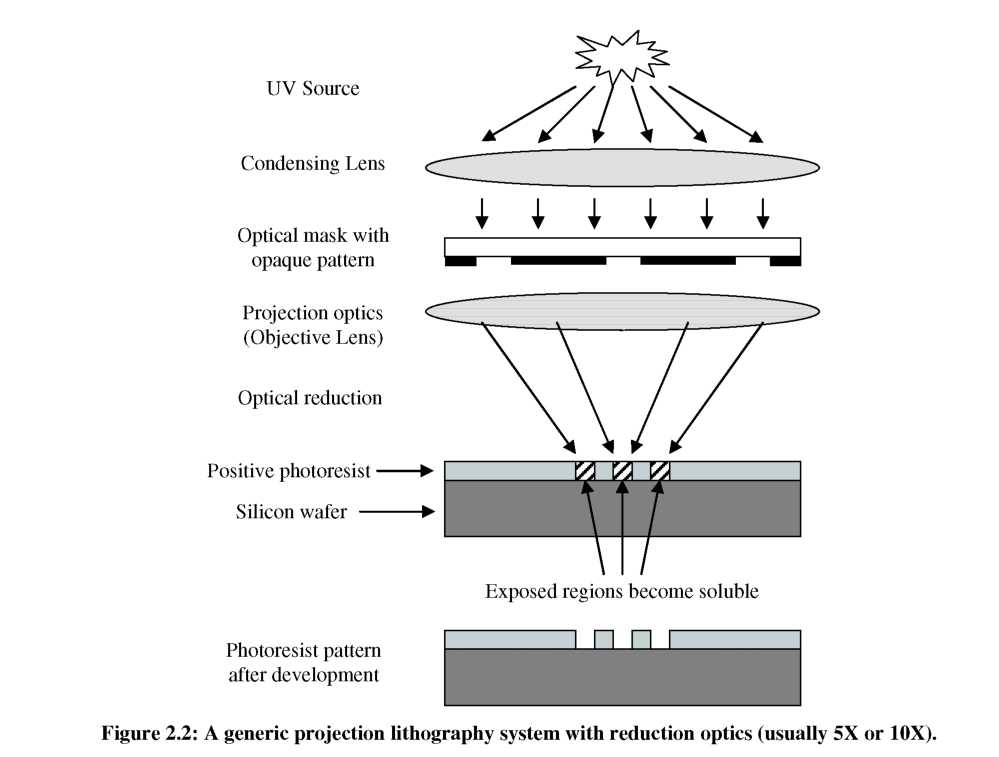
The chosen method of pixilated gray-scale lithography relies on a standard projection lithography system, a simplified schematic of which is shown in Figure 2.2. When a pixilated optical mask is placed in this system, a fraction of the incident light is blocked and transmitted light will diffract. It is this diffraction between closely spaced opaque pixels that leads to a uniform intermediate intensity at the wafer surface.

To understand this phenomenon more closely, we will follow the reasoning of Henke et al [4, 5], where we consider the projection optics (objective lens) to act as a spatial frequency filter on a one dimensional grating, such as set of chrome lines, with a pitch of p. We can define the amplitude transmission function of the mask as T(x), where the values 0 and 1 are assigned to locations on the mask with or without chrome, respectively. The Fourier spectrum, T’(k), of this amplitude transmission function, T(x), is obtained through the standard Fourier relations:

(1)

and

(2)

A diffraction limited optical system will cut off higher spatial frequencies in the Fourier spectrum, T’(k). Thus, the complex amplitude, A(x’), in the image plane (i.e. at the wafer surface), is given by:

(3)

The parameter k refers to a lateral wave vector on the mask, whose 1^st diffraction order corresponds to:

(4)

where  is the wavelength of illumination light used in the stepper and и is a spatial frequency of the grating lines. The numerical aperture (NA) of the system then defines the maximum angle, _c, capable of passing through the system:

(5)

For normal incidence plane wave illumination, this NA determines the critical spatial frequency, v_c, or critical pitch, p_c, necessary on the optical mask for the 1^st diffraction order to reach the critical angle, :

(6)

For periodic features below this critical pitch, the ±1 and higher diffraction orders are prevented from passing through the projection system. Since all spatial information is contained in the higher diffraction orders, only a uniform ‘DC’ component of light (0^th diffraction order) is transmitted through the optical system, and all spatial information regarding the shape of individual pixels is lost. In a true lithography system, the partial coherence of the light source, , will also play a role in determining the critical pitch of the system [5]:

(7)

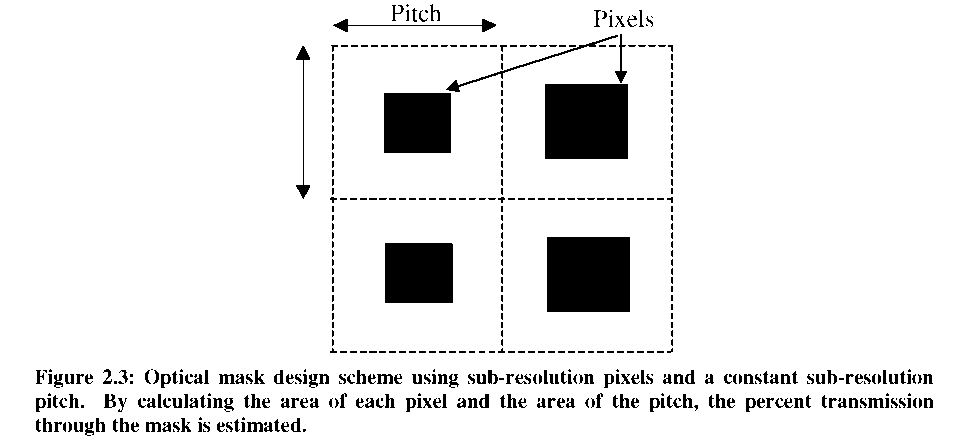
For the research performed in this dissertation, the pitch has been held constant, at or near the critical pitch in order to maintain this condition. The ‘DC’ component of the optical mask transmission was then locally modulated by varying the size of rectangular sub-resolution opaque pixels contained therein, as shown in Figure 2.3.

Now, the complex amplitude at the wafer surface can be determined by a simple integral over the mask transmission function, which only includes k=0:

(8)

For a pixilated approach, this integral calculates the percentage of light transmitted through the optical mask (Tr), which can be calculated using the area of each pixel (A_pixel) and the area of the square pitch (A_pitch):

(9)

(10)