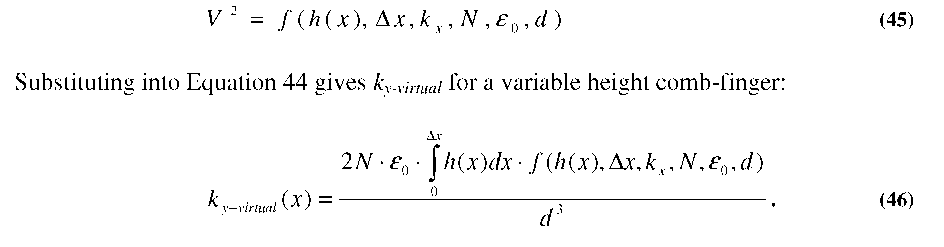- •Brian Carl Morgan, Doctor of Philosophy, 2006
- •1. Introduction
- •Introduction
- •Passive Techniques
- •Active Techniques
- •Thesis Objectives and Structure
- •Chapter 2: gray-scale technology
- •Introduction
- •Gray-scale Background
- •Theoretical Background
- •Optical Mask Constraints
- •Standard Lithography Process
- •Design and Lithography Advancements
- •Minimum Feature Limitations
- •2.3.3. Double Exposures
- •Pattern Transfer
- •Deep Reactive Ion Etching (drie)
- •Selectivity Characterizations
- •Technology Collaborations
- •Phase Fresnel Lens (nasa)
- •2.5.2.1. Compensated Aspect Ratio Dependent Etching (carde)
- •Conclusion
- •Chapter 3: elect rostatic comb-drives using goay-scale technology
- •Introduction
- •Electrostatic Actuation Fundamentals
- •Tailored Comb-finger Design and Simulation
- •Analytical Displacement Simulations (2-d)
- •Finite Element Analysis (3-d)
- •Instability Considerations
- •Reduced Height Suspensions
- •Fabrication
- •Comb-drive Testing
- •Reduced Height Comb-fingers
- •Conclusion
- •Introduction
- •Tunable mems Resonator Operation
- •1. Introduction 1
- •1.1. Introduction 1
- •2.1. Introduction 11
- •3.1. Introduction 36
- •4.1. Introduction 51
- •Gray-scale Electrostatic Springs
- •Testing and Characterization
- •Conclusion
- •Introduction
- •Device Concept
- •Figure 5.5: Calculated coupling as two co-axial single-mode fibers are separated longitudinally.
- •Figure 5.6: Alignment schematic for a bent fiber cantilever coupling to a fixed output fiber.
- •Alignment Wedges
- •Fabrication
- •Assembly
- •Actuation Concept Demonstration
- •Introduction
- •Experimental Setup
- •Static Testing
- •Table 6.3: Measured fiber locations for discrete actuation voltages. These 4 points form the corners of a diamond shaped alignment area.
- •Channel a (va2)
- •1. Introduction 1
- •1.1. Introduction 1
- •2.1. Introduction 11
- •3.1. Introduction 36
- •4.1. Introduction 51
- •Horizontal displacement
- •Voltage Squared (v2)
- •Auto-alignment Algorithms
- •Figure 6.16: Simplified hill-climbing algorithm block diagram.
- •Automated Fiber Alignment Results
- •Settling Time, Coarse Threshold Power (%Peak)
- •Testing Summary and Discussion
- •Conclusion
- •Summary of Accomplishments
- •Future Work
Instability Considerations
One issue that has been ignored to this point is the stability of the comb-drive actuator. In the analysis presented in Section 3.2, it was assumed that all forces in the y- direction (perpendicular to the stroke) will cancel. However, that assumption is premised on the moving comb-fingers being exactly У2 way between the stationary fingers. In reality, the comb-fingers are always slightly off-center and the force in the y-direction is:
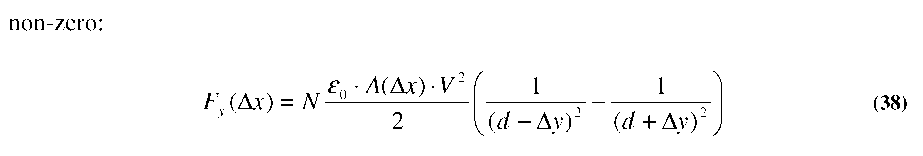
We can now define a virtual spring constant in the y-direction (ky-virtual) as the derivative of Fy with respect to y, evaluated at the Ay=0 (center) position:
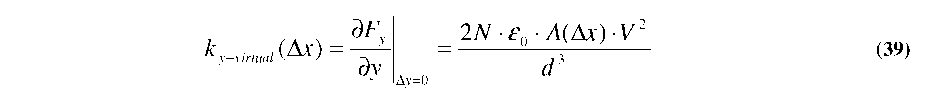
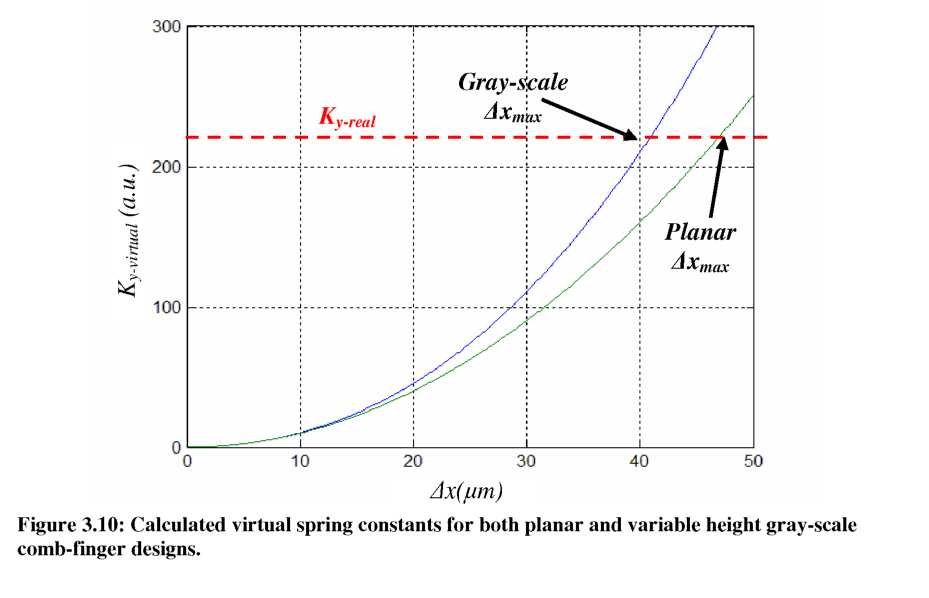
we set ky.virtual = ky-real, we can find the maximum stable deflection point (Axmax). For the case of a traditional, planar comb-drive, we start by re-arranging Equation 30 to be:
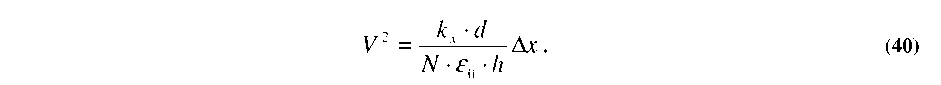
Substituting this V expression into Equation 39 (set to ky-real), and using the fact that for the planar case A(x)=h-Ax, yields:
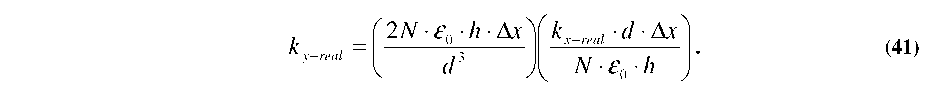
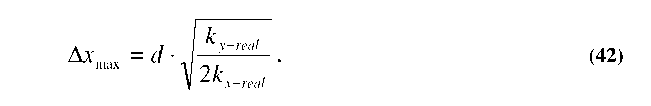
For the case of a gray-scale tailored comb-finger however, Equation 42 is no longer applicable. Since the height is now a function of displacement, we must write A(Ax) as an integral:


Similarly, Equation 40 no-longer holds as the V (x) relationship is now a complicated function dependent on h(x), Ax, kx, N, e0, and d: