2. Finite Element Analysis (3-d)

The glaring difference between the planar and variable height case is the

importance of fringing fields, which are neglected in planar devices. Given the dimensions and aspect ratios involved, simply reducing the height by 50% will not reduce the capacitance at each comb-position by exactly 50%. Thus, our parallel plate model must be extended to include the effects of fringing fields on the capacitance-position profiles to accurately predict actuator behavior using Finite Element Analysis (FEA). During our simulation, limitations imposed by fabrication processes must be considered, as achievable comb-finger gaps and feature aspect ratios will be fabrication dependent. Our analysis and designs will continue to assume 100pm SOI wafers and 10:1 feature aspect ratios, giving an initial gap of d=10^m as done before.

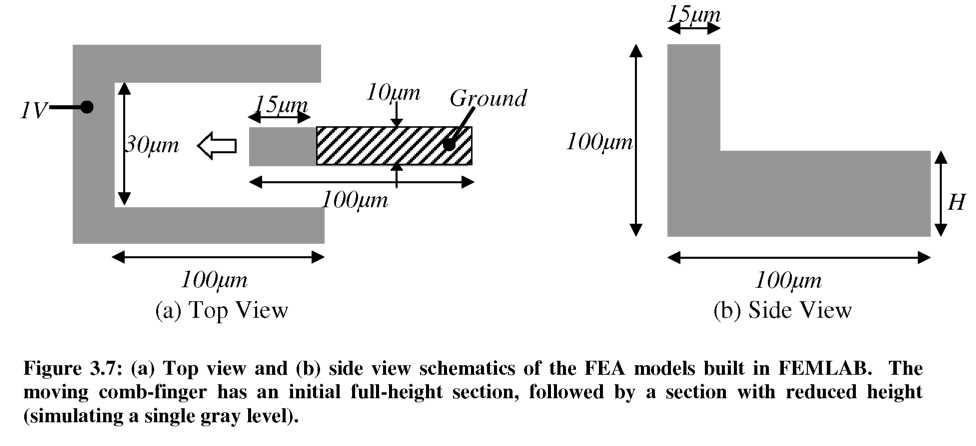
FEA models were constructed in the FEMLAB (V3.0) Electrostatics Module to emulate a grounded, variable height comb-finger moving between two stationary comb- fingers (held at a potential of V=1 Volt). The behavior of a device with N comb-pairs was estimated by multiplication. Top and side view schematics of the basic model geometry simulated are shown in Figure 3.7. While h(x) ^ 1/Ax profiles were discussed earlier for intuition, it will be shown that fringing fields cause a height step to act in a similar manner. All comb-fingers were 100pm long with a maximum height of 100pm. The moving comb-finger has an initial 15 pm full-height section, followed by 85 pm long section with a reduced constant height, H. A ground plane was included 10pm below the comb-fingers to simulate a grounded substrate below the moving fingers. The system was bounded by a 3mm by 3mm grounded box. A mesh containing approximately 200K elements was found to be sufficient to ensure convergence of our solution.

Rather than solve the Laplace equation (V ²V = 0) directly, FEMLAB was used to minimize total system energy in order to find the voltage distribution. This distribution specifies the electric field, and therefore electric energy density, in each discrete element. By integrating over the volume, the total electric potential energy of the system was obtained. The capacitance is then calculated using this total electric potential energy and the applied potential of 1V in Equation 25. The FEA simulated capacitance as a function of comb-finger overlap is shown in Figure 3.8 for values of H = 100p,m (planar), H=40p,m, and H=10p,m. While the absolute value of capacitance will be different for each case, all curves were shifted vertically to a common origin to ease interpretation. This does not effect the force profiles since they depend only on the derivative.

a function of position. As evident in Figure 3.9, the planar case results in a constant force that is independent of position, consistent with the simple parallel plate model.

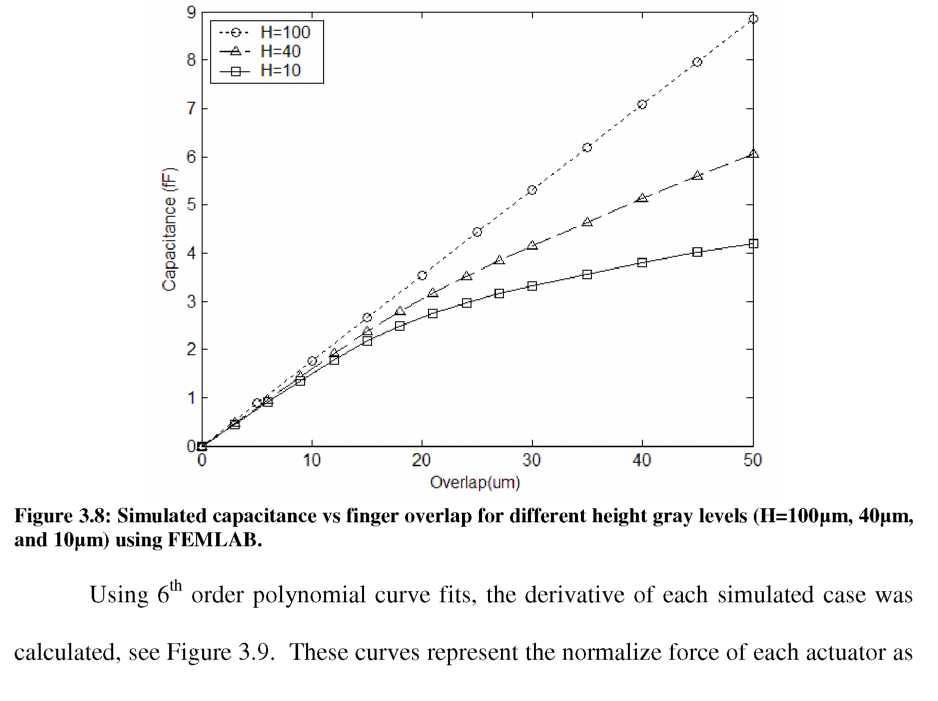
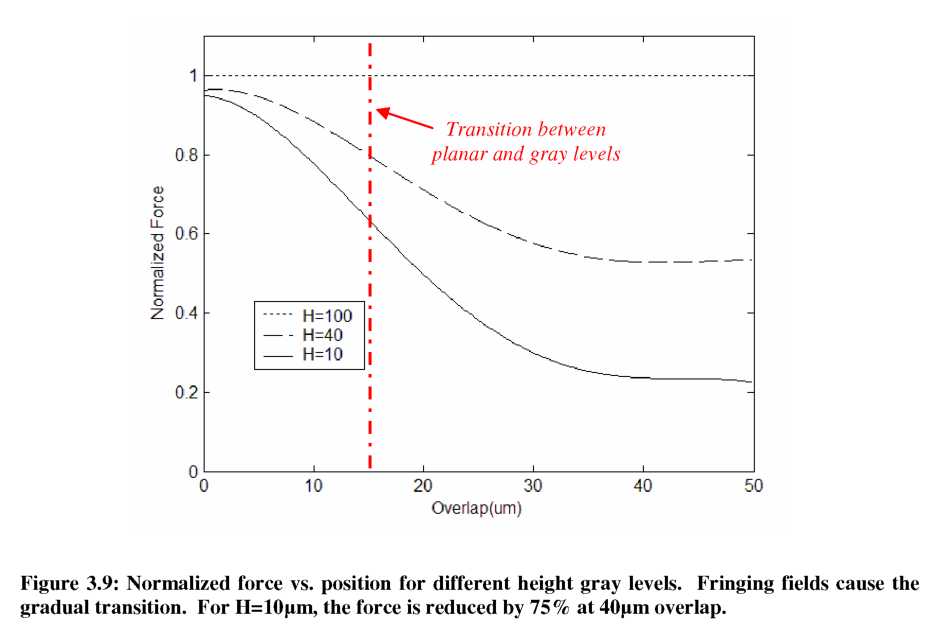
From the FEA simulation results, we see that the effects of fringing fields on the capacitance profile are significant. If a parallel-plate approximation was sufficient for the variable-height case, the normalized force profile would resemble the stepped height profile, h(x), shown in the side view of Figure 3.9. However, the fringing fields and our FEA model are able to “see” the change in height far before the reduced-height section arrives between the stationary fingers at an overlap of 15pm. Consequently, the force profile changes gradually around the transition point, and eventually settles to a smaller constant value. For the case of H=10pm, the total force is reduced by 75%, which should cause a corresponding improvement in displacement resolution of the actuator. Both the

analytical and FEA simulated force profiles will be compared to the experimental results of the fabricated gray-scale actuators in Section 3.6.1.