2.3. Обратный код

Обратный код–метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения над натуральными числами. Ранее метод использовался в механических калькуляторах (арифмометрах). В настоящее время используется в основном в современной компьютерной технике.

Обратный n-разрядный двоичный код положительного целого числа состоит из одноразрядного кода знака (двоичной цифры 0), за которым следует (n − 1)-разрядное двоичное представление модуля числа (обратный код совпадает с прямым кодом).

Обратный n-разрядный двоичный код отрицательного целого числа состоит из одноразрядного кода знака (двоичной цифры 1), за которым следует (n − 1)-разрядное двоичное число, представляющее собой инвертированное (n − 1)-разрядное представление модуля числа.

У числа 0 имеется два обратных кода: «положительный нуль» 00000000 и «отрицательный нуль» 11111111 (приведены 8-разрядные обратные коды).

n-разрядный обратный код позволяет представить числа в диапазоне .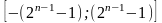

Примеры представления чисел

Десятичный код	Двоичный код	8-разрядный прямой код
0 -0 5 -5	0 0 101 -101	00000000 11111111 00000101 11111010

2.4. Дополнительный код

Дополнительный код– наиболее распространенный способ представления отрицательных целых чисел в компьютерной арифметике. Он позволяет заменить операцию вычитания на операцию сложения, чем упрощает архитектуру ЭВМ. Дополнительный код отрицательного числа получается инвертированием двоичного числа и прибавлением к нему единицы.

При записи числа в дополнительном коде, старший разряд является знаковым. Если его значение равно 0, то в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом. Если же знаковый разряд равен 1, то в остальных разрядах записано отрицательное двоичное число, преобразованное в дополнительный код. Для получения значения отрицательного числа все разряды, кроме знакового, инвертируются, а к результату добавляется единица. Обратное преобразование, то есть перевод из дополнительного в прямой код, осуществляется аналогично.

Двоичное 8-разрядное число может представлять любое целое в диапазоне от −128 до +127. Если старший разряд равен нулю, то наибольшее целое число, которое может быть записано в оставшихся 7 разрядах равно .

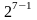Примеры представления чисел

Десятичный код	8-разрядный двоичный
	прямой код	дополнительный код
0 1 -1 -10	00000000 00000001 10000001 10001010	00000000 00000001 11111111 11110110

Примеры преобразования чисел

Преобразуем отрицательное число −5, записанное в прямом коде, в дополнительный.

1.	Прямой код числа −5, взятого по модулю	101
2.	Инвертируем все разряды числа, получая таким образом обратный код	010
3.	Добавим к результату 1 и допишем знаковый единичный разряд	1011

Для обратного преобразования используется тот же алгоритм.

1.	Дополнительный код числа −5	1011
2.	Инвертируем все разряды числа, получая таким образом обратный код	100
3.	Добавим к результату 1	0101
4.	Проверим результат, сложив с дополнительным кодом (пятый разряд суммы отбрасывается)	0101 + 1011 = 10000

Тот же принцип можно использовать и в компьютерном представлении десятичных чисел: для каждого разряда цифра X заменяется на 9−X, и к получившемуся числу добавляется 1. Например, при использовании четырёхзначных чисел −0081 заменяется на 9919 (9919+0081=0000, пятый разряд выбрасывается).