Вычисление производной функции, заданной неявно.

Производная вычисляется по основным правила дифференцирования, считая, что функция y зависит от переменной x.

Пример. Вычислить производную функции заданной неявно

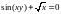
Решение.

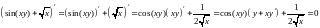
Выражая из последнего равенства 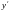получим:

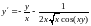
Производная степенно-показательной функции.

При дифференцировании функций, состоящих из большого количества множителей, или функций вида 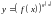рекомендуется предварительное логарифмирование.

Пример. Найти производную функции

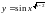
Решение.

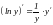
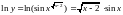
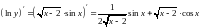
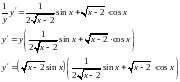
Производная обратной функции.

Пусть требуется найти производную функции у = f(x) при условии, что обратная ей функция x = g(y) имеет производную, отличную от нуля в соответствующей точке.

Для решения этой задачи дифференцируем функцию x = g(y) по х:

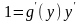
т.к. g(y)  0

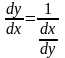
т.е. производная обратной функции обратная по величине производной данной функции.

Исследование функции на монотонность и экстремум, наибольшее и наименьшее значение.

О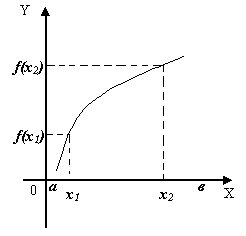 пределение.Функция f(x) называется возрастающей на отрезке (а, в), если для любых х₁ и х₂, взятых на этом отрезке таких, что х₁ < х₂ , имеет место неравенство: f(x₁) < f(x₂).

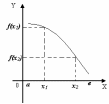
Определение. Функция f(x) называется убывающей на отрезке (а, в), если для любых х₁ и х₂, взятых на этом отрезке таких, что х₁ < х₂ , имеет место неравенство: f(x₁) > f(x₂).

Определение. Только возрастающие, или убывающие функции называются монотонными, а промежутки, на которых она монотонна – промежутками монотонности.

Пример. Исследовать функцию 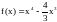на монотонность и экстремумы.

Решение.

Функция дифференцируема на всей числовой оси.

1)Вычислить производную функции .

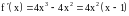2) Решить уравнение

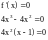
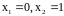– критические точки.

3) Найти знаки производной на промежутках .

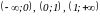4) Сделать выводы о характере монотонности и наличии экстремумов:

Функция возрастает на промежутке 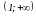, убывает на .

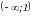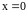
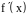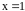при переходе через точку не меняет своего знака, поэтому эта точка не является точкой экстремума. При переходе через точку меняет свой знак с «–» на «+», следовательно, – точка минимума (на рисунке получается «впадина»). Вычислим значение функции при : 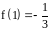– минимум.

Ответ: Функция возрастает на промежутке , убывает на . – точка минимума, – минимум.

Задачи для решения Тема: «Функция. Ее свойства и график».

Вопросы:

• Понятие функции.

• Область определения и множество значений функции.

• Четность и нечетность функции.

• Монотонность функции.

• Выпуклость и вогнутость функции.

• Асимптоты.

В результате изучения темы слушатели должны уметь:

• Находить область определения функции.

• Исследовать на четность и нечетность функции.

• Исследование функции на монотонность и выпуклость с помощью производной.

• Находить асимптоты.

• Строить графики функций.

Эти вопросы рассмотрены в [1],[3] и в [2],[3] приведены примеры решений типовых задач.

[1] Глава 4. Функции одной переменной. Стр. 69-103.