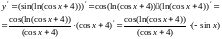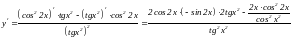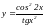- •Часть 1
- •Предисловие
- •Указания по выполнению и оформлению контрольной работы.
- •Тема: «Основы линейной алгебры»
- •Глава 5. Основы линейной алгебры. Стр. 130-171.
- •Основные понятия.
- •Свойства матриц.
- •Свойства определителей.
- •Системы линейных алгебраических уравнений.
- •Векторы.
- •Уравнение прямой и плоскости в пространстве.
- •Тема: «Предел функции»
- •Глава 11. Предел и непрерывность функций нескольких переменных. Стр. 275-283.
- •Предел функции.
- •Специальные пределы.
- •Тема «Производная функции и ее приложения».
- •Глава 7. Дифференциальное исчисление функции одной независимой переменной. Стр. 190-235. Задачи, приводящие к понятию производной.
- •Основные правила нахождения производной. Таблица производных
- •Вычисление производной функции.
- •Вычисление производной сложной функции.
- •Вычисление производной функции, заданной неявно.
- •Производная степенно-показательной функции.
- •Производная обратной функции.
- •Исследование функции на монотонность и экстремум, наибольшее и наименьшее значение.
- •Задачи для решения Тема: «Функция. Ее свойства и график».
- •Глава 6. Применение дифференциального исчисления к исследованию функций. Стр. 127-158.
- •Глава 5. Дифференцирование. Стр. 54-81.
- •Глава 7. Дифференциальное исчисление функции одной независимой переменной. Стр. 190-235. Общая схема исследования функции. Построение графиков
- •Тема: «Интегрирование функции».
- •Глава 8. Определенный интеграл. Стр. 177-221.
- •Глава 8. Определенный интеграл. Стр. 221-260.
- •Глава 10. Определенный интеграл. Стр. 296-325. Понятие и основные свойства неопределенного интеграла
- •Формулы интегрирования
- •Метод непосредственного интегрирования
- •Интегрирование методом замены переменной
- •Интегрирование по частям
- •Определенный интеграл и его приложения
- •Основные свойства определённого интеграла
- •Геометрический смысл определённого интеграла
- •Физический смысл определённого интеграла
- •Задания для контрольной работы.
- •Оглавление
- •Литература
Тема «Производная функции и ее приложения».
Вопросы:
Задачи, приводящие к понятию производной.
Понятие производной.
Правила вычисления производной.
Производная сложной функции.
Промежутки монотонности. Возрастание и убывание функции.
Экстремум функции.
Таблица производных.
В результате изучения темы слушатели должны уметь:
вычислять производную,
исследовать функцию на возрастание и убывание, используя производную,
находить экстремум функции.
Эти вопросы рассмотрены в [1],[3],[5] и в [2],[3],[5] приведены примеры решений типовых задач.
[1] Глава 5. Дифференцирование. Стр. 104-126.
[2] Глава 5. Дифференцирование. Стр. 54-81.
[3] Глава 5. Введение в анализ. Стр. 97-185.
[5] Глава 6. Введение в анализ. Стр. 172-189.
Глава 7. Дифференциальное исчисление функции одной независимой переменной. Стр. 190-235. Задачи, приводящие к понятию производной.
Задача
о скорости. Пешеход
движется прямолинейно. Положение его
траектории определяется ее абсциссой,
которая будет функцией времени
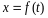 .
Пусть в момент времени
.
Пусть в момент времени
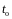 пешеход
занимает положение
пешеход
занимает положение
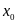 ,
за время
,
за время
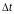 он переместиться в точку
он переместиться в точку
 тогда за это время пешеход пройдет путь
тогда за это время пешеход пройдет путь
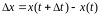 .
Средняя скорость пешехода определяется
по формуле
.
Средняя скорость пешехода определяется
по формуле
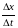 за время
за время
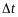 .
Тогда средняя скорость в момент времени
.
Тогда средняя скорость в момент времени
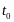 определяется по формуле:
определяется по формуле:

Задача о касательной.
З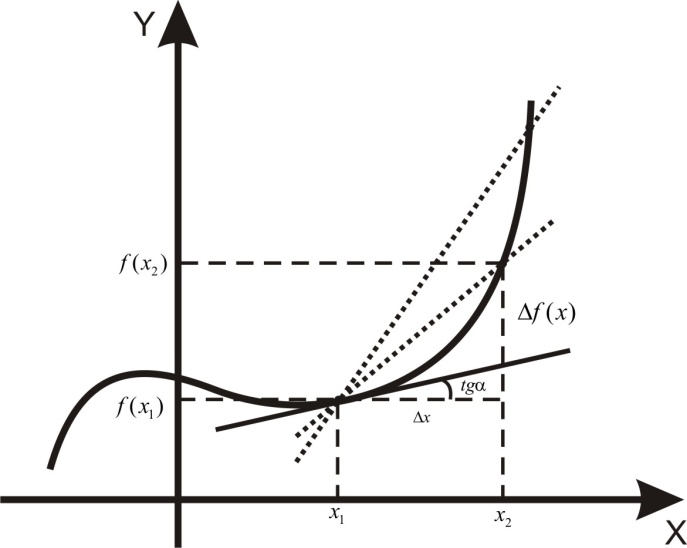 адан
график функции
адан
график функции
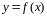 .
В точке
.
В точке
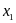 требуется написать уравнение касательной.
Построим касательную: возьмем две точки
на графике функции и проведем через
них секущую. Устремим точку
требуется написать уравнение касательной.
Построим касательную: возьмем две точки
на графике функции и проведем через
них секущую. Устремим точку
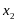 к
к
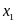 .
Тогда секущая будет приближаться к
касательной. Таким образом касательная
– есть предельное положение секущих.
Тангенс угла наклона касательной можно
вычислить по формуле
.
Тогда секущая будет приближаться к
касательной. Таким образом касательная
– есть предельное положение секущих.
Тангенс угла наклона касательной можно
вычислить по формуле
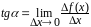 .
Уравнение касательной имеет вид
.
Уравнение касательной имеет вид
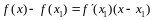 .
.
Определение.
Производной
функции
называется предел отношения приращения
функции, к вызвавшему это приращение
приращению аргумента.
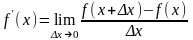
Основные правила нахождения производной. Таблица производных
Обозначения:
с
– постоянная, u,
v – функции,
дифференцируемые в
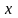 .
.
(c)' = 0, где с – постоянное число,
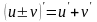 ,
,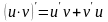
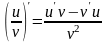
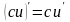
Производные основных элементарных функций.
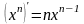
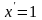 – (частный случай
формулы 1)
– (частный случай
формулы 1)
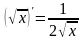 –
(частный случай
формулы 1)
–
(частный случай
формулы 1)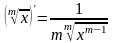 –
(частный случай
формулы 1)
–
(частный случай
формулы 1)

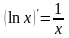
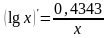
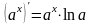
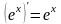

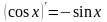
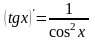
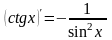
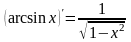
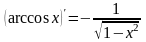
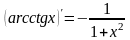
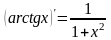
Вычисление производной функции.
Пример.
Найти производную функции
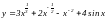 .
.
Решение. Воспользуемся правилами: производная от суммы (разности) равна сумме (разности) производных, константу можно выносить из под знака производной:
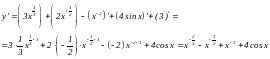
Пример. Найти производную функции у =х4·ех.
Решение.
Воспользуемся
правилом вычисления производной
произведения:
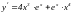 .
.
Пример.
Найти производную функции
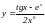 .
.
Решение. Воспользуемся правилом вычисления производной частного:
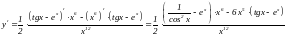 .
.
Вычисление производной сложной функции.
Если
у = f(u),
где u =
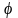 (x),
т. е.
если у
зависит от
х через
посредство промежуточного аргумента
u, то
у называется
сложной функцией от х, функцию f называют
внешней функцией, а
функцию
– внутренней.
(x),
т. е.
если у
зависит от
х через
посредство промежуточного аргумента
u, то
у называется
сложной функцией от х, функцию f называют
внешней функцией, а
функцию
– внутренней.
Производная сложной функции равна произведению производной внешней функции на производную внутренней функции:
у ' = f '(u)· u '(х).
Пример. Вычислить производную функции
 .
.
y' = [(x2 – 1)-4] ' = -4(x2 – 1)-4-1·(x2 – 1) ' = -4(x2 – 1)-5·2x = -8x (x2 – 1)-5.
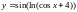 Это сложная
функция (трехуровневая)
Это сложная
функция (трехуровневая)