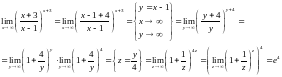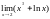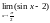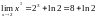- •Часть 1
- •Предисловие
- •Указания по выполнению и оформлению контрольной работы.
- •Тема: «Основы линейной алгебры»
- •Глава 5. Основы линейной алгебры. Стр. 130-171.
- •Основные понятия.
- •Свойства матриц.
- •Свойства определителей.
- •Системы линейных алгебраических уравнений.
- •Векторы.
- •Уравнение прямой и плоскости в пространстве.
- •Тема: «Предел функции»
- •Глава 11. Предел и непрерывность функций нескольких переменных. Стр. 275-283.
- •Предел функции.
- •Специальные пределы.
- •Тема «Производная функции и ее приложения».
- •Глава 7. Дифференциальное исчисление функции одной независимой переменной. Стр. 190-235. Задачи, приводящие к понятию производной.
- •Основные правила нахождения производной. Таблица производных
- •Вычисление производной функции.
- •Вычисление производной сложной функции.
- •Вычисление производной функции, заданной неявно.
- •Производная степенно-показательной функции.
- •Производная обратной функции.
- •Исследование функции на монотонность и экстремум, наибольшее и наименьшее значение.
- •Задачи для решения Тема: «Функция. Ее свойства и график».
- •Глава 6. Применение дифференциального исчисления к исследованию функций. Стр. 127-158.
- •Глава 5. Дифференцирование. Стр. 54-81.
- •Глава 7. Дифференциальное исчисление функции одной независимой переменной. Стр. 190-235. Общая схема исследования функции. Построение графиков
- •Тема: «Интегрирование функции».
- •Глава 8. Определенный интеграл. Стр. 177-221.
- •Глава 8. Определенный интеграл. Стр. 221-260.
- •Глава 10. Определенный интеграл. Стр. 296-325. Понятие и основные свойства неопределенного интеграла
- •Формулы интегрирования
- •Метод непосредственного интегрирования
- •Интегрирование методом замены переменной
- •Интегрирование по частям
- •Определенный интеграл и его приложения
- •Основные свойства определённого интеграла
- •Геометрический смысл определённого интеграла
- •Физический смысл определённого интеграла
- •Задания для контрольной работы.
- •Оглавление
- •Литература
Тема: «Предел функции»
Вопросы:
Понятие предела.
Свойства пределов.
Первый и второй замечательный предел.
Правила вычисления пределов.
В результате изучения темы слушатели должны уметь:
Вычислять пределы.
Эти вопросы рассмотрены в [1],[3],[5] и в [2],[3],[5] приведены примеры решений типовых задач.
[1] Глава 4. Функции одной переменной. Стр. 69-103.
Глава 11. Предел и непрерывность функций нескольких переменных. Стр. 275-283.
[2] Глава 11. Понятие, предел и непрерывность функций нескольких переменных. Стр. 179-183.
[3] Глава 5. Введение в анализ. Стр. 97-185.
[5] Глава 6. Введение в анализ. Стр. 172-189.
Предел функции.
Определение.
Пределом
функции
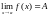 называется такое число А, что
называется такое число А, что
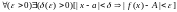
Предел непрерывной функции. Предел непрерывной функции равен значению функции в заданной точке.
Если
существуют конечные пределы
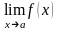 и
и
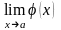 ,
то
,
то
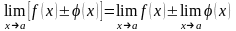 ,
,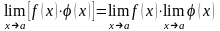 ,
,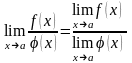 .
.Константу можно выносить из под знака предела
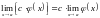
Предел константы равен константе.
Предел
многочлена:
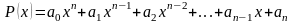 при
при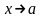 равен
значению этого многочлена при
равен
значению этого многочлена при
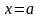 ,
т. е.
,
т. е.
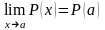
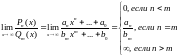
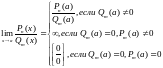
Специальные пределы.
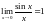 -
1-ый замечательный предел. Первый
замечательный предел можно обобщить
и записать в виде:
-
1-ый замечательный предел. Первый
замечательный предел можно обобщить
и записать в виде:
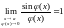
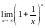 =
=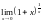 =е=2,71828…2-ой
замечательный предел. Общий вид второго
замечательного предела:
=е=2,71828…2-ой
замечательный предел. Общий вид второго
замечательного предела:
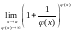 =
=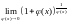 =е
=е
Следствия:
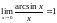 ,
,
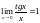 ,
,
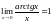
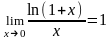 ,
,
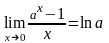 ,
,
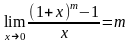 .
.
При вычислении пределов следует учитывать, что:
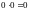
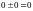
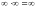
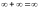
И
могут получиться неопределенности,
когда ничего о значении предела сказать
нельзя:
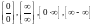 ,
,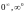
Примеры решения типовых задач:
Пример. Найти предел функций:
Решение.
Так как функции непрерывны, то предел функции равен значению функции в этой точке.
Пример.
Найти предел функции:
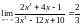 ,так как
,так как
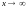 ,
а степени многочленов в числителе и
знаменателе одинаковые, следовательно
предел равен отношению коэффициентов
при старших степенях.
,
а степени многочленов в числителе и
знаменателе одинаковые, следовательно
предел равен отношению коэффициентов
при старших степенях.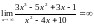 ,так
как
,
а степень многочлена в числителе
больше, чем степень многочлена в
знаменателе.
,так
как
,
а степень многочлена в числителе
больше, чем степень многочлена в
знаменателе.
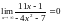 ,так
как
,
а степень многочлена в знаменателе
больше, чем степень многочлена в
числителе.
,так
как
,
а степень многочлена в знаменателе
больше, чем степень многочлена в
числителе.
Пример. Найти предел функции.
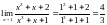
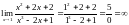
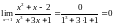
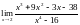 Следующий пример
дает неопределенность
Следующий пример
дает неопределенность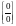 поэтому число 2 является корнем
многочлена, стоящего в числителе и
знаменателе. Тогда эти многочлены
можно разложить на множители. По формуле
разности квадратов
поэтому число 2 является корнем
многочлена, стоящего в числителе и
знаменателе. Тогда эти многочлены
можно разложить на множители. По формуле
разности квадратов
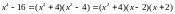
Для разложение многочлена, стоящего в числителе на множители мы можем применить метод группировки или поделить многочлен на многочлен «в столбик».
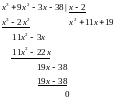
Тогда
получим
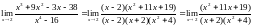
Полученная дробь уже не дает неопределенности и для вычисления ее предела мы можем подставить число 2:
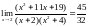
Пример. Вычислить пределы:

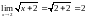 предел непрерывной
функции равен значению функции в этой
точке.
предел непрерывной
функции равен значению функции в этой
точке.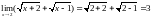 предел непрерывной
функции равен значению функции в этой
точке.
предел непрерывной
функции равен значению функции в этой
точке.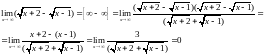
В
случае неопределенности типа
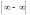 нужно перейти к неопределенности типа
или
нужно перейти к неопределенности типа
или
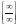 ,
для этого домножим числитель и знаменатель
дроби на сопряженное выражение.
,
для этого домножим числитель и знаменатель
дроби на сопряженное выражение.
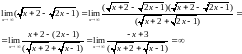 так
как степень числителя больше степени
знаменателя, то по рассмотренному
ранее правилу мы получаем, что предел
равен бесконечности..
так
как степень числителя больше степени
знаменателя, то по рассмотренному
ранее правилу мы получаем, что предел
равен бесконечности..
Пример. Вычислить пределы:
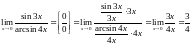 При подстановке
значения переменно получается
неопределенность типа
При подстановке
значения переменно получается
неопределенность типа
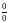 ,
поэтому непосредственной подстановкой
результат вычислений быть получен не
может. Поэтому для его вычисления
используем первый замечательный
предел и следствие из него.
,
где
,
поэтому непосредственной подстановкой
результат вычислений быть получен не
может. Поэтому для его вычисления
используем первый замечательный
предел и следствие из него.
,
где
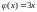 ,
,
 ,
где
,
где
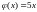 .
.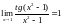 .
При непосредственной подстановки
значения переменной получается
неопределенность типа
.
Данный предел является непосредственным
первого замечательного предела, где
в качестве
.
При непосредственной подстановки
значения переменной получается
неопределенность типа
.
Данный предел является непосредственным
первого замечательного предела, где
в качестве
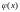 берется функция
берется функция
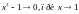 .
.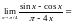 при подстановке
значения переменной получается
неопределенность типа
,
поэтому для вычисления предела
необходимы дополнительные преобразования:
при подстановке
значения переменной получается
неопределенность типа
,
поэтому для вычисления предела
необходимы дополнительные преобразования:
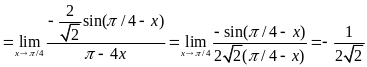
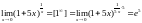 При непосредственном
вычислении получается неопределенность
типа
При непосредственном
вычислении получается неопределенность
типа
 ,
поэтому для его вычисления мы
воспользовались вторым замечательным
пределом
,
поэтому для его вычисления мы
воспользовались вторым замечательным
пределом