Уравнение прямой и плоскости в пространстве.
Определение. Плоскость () в пространстве с заданной декартовой прямоугольной системой координат может быть задана одним из следующих уравнений: Ax + By + Cz + D = 0 – общее уравнение плоскости;
Условие параллельности плоскостей
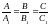.Условие перпендикулярности плоскостей
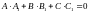.Неполные уравнения плоскостей:
D=0 начало координат принадлежит плоскости;
A=0 плоскость параллельна оси OX;
B=0 плоскость параллельна оси OY;
C=0 плоскость параллельна оси OZ;
B=C=0 плоскость параллельна OYZ;
A=B=0 плоскость параллельна OXY;
A=C=0 плоскость параллельна OXZ;
A(x
– x0)
+ B(y – y0)
+ C(z – z0)
= 0 – уравнение плоскости (),
проходящей
через точку M(x0; y0; z0)
и перпендикулярной вектору
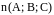– вектору нормали к ()
( вектором нормали к плоскости ()
называется любой ненулевой вектор,
перпендикулярный ());
– уравнение
плоскости в отрезках,
где a, b, c –направленные отрезки,
отсекаемые плоскостью на осях 0x, 0y, и
0z соответственно;
Уравнение плоскости, проходящей через три точки M1(x1;y1;z1), M2(x2;y2;z2), M3(x3; y3; z3), не лежащие на одной прямой.
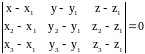
Расстояние от точки M0(x0; y0; z0) до плоскости (), заданной общим уравнением Ax + By + Cz + D = 0, находится по формуле:
.
Угол
между плоскостями
(1):
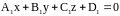и (2):
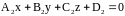есть угол между нормалями
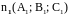и
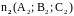(с поправкой на направление, если угол
тупой) к этим плоскостям:
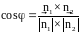
или по формуле
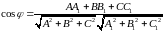
Эти плоскости:
параллельны в том и только в том случае, есл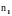и
и
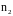коллинеарны;
перпендикулярны в том и только в том случае, если
.
Определение. Прямая (L) в пространстве с заданной прямоугольной системой координат может быть задана:
Если
имеется точка
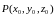и направляющий вектор
.
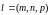Тогда уравнение прямой можно записать
в виде:
.
Уравнение
прямой по
двум точкам
,
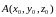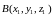имеет вид
.
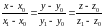параметрическими
уравнениями
,
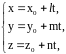
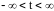заданные числа x0,
y0,
z0,
l,
m, n имеют тот же смысл, что и в канонических
уравнениях;
общим уравнением
при этом (L) есть прямая пересечения плоскостей (1): , (2): .
Если уравнение прямой заданно как пересечение плоскостей, то направляющий вектор вычисляется по формуле:
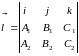
Угол
между прямыми (L1)
и (L2)
есть угол между направляющими векторами
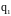и
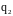(с поправкой на направление, если
угол между ними тупой):
.
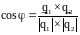Или по формуле:
.
Угол
между прямой (L):
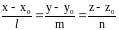и плоскостью
():
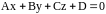определяется по формуле
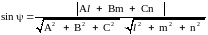
Пример. Даны вершины тетраэдра A(2,3,1),B(4,1,-2),C(6,3,7), D(-5,-4,8).
Найти:
длину ребра AB;
угол между ребрами AB и AD;
угол между ребром AD и плоскостью ABC;
объем тетраэдра ABCD;
уравнение ребра AB;
уравнение плоскости ABC;
уравнение высоты, опущенной из D на ABC;
проекцию точки D на ABC;
длину высоты DO.
Решение.
1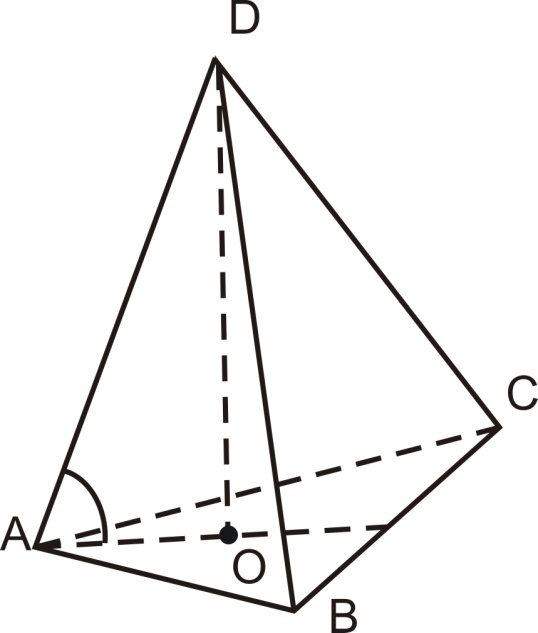
.
Вычислим расстояние между точками
.
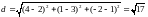2. Угол между векторами вычислим используя формулу для скалярного произведения.
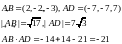
Подставляя
в формулу получим
.
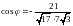3. Угол между ребром и плоскостью вычисляется по формуле:
,
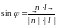где
-
вектор нормали к плоскости,
-
направляющий вектор прямой.
Направляющий
вектор прямой совпадает с вектором
и, следовательно с учетом предыдущего
пункта
.
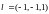Для
нахождения вектора, ортогонального
плоскости, нам надо найти вектор
ортогональный двум векторам из (ABC),
в качестве таких векторов возьмем
и
.
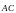Вектор, полученный в результате векторного произведения этих векторов и будет искомым вектором.
,
.
.
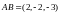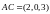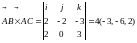
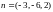Поставляя
в формулу получим:
.
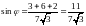4. Для нахождения тетраэдра воспользуемся формулой через смешанное произведение.
,
,
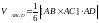
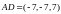
Вычисляя смешанное произведение получим
.
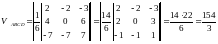5. Для нахождения уравнения мы можем воспользоваться формулой для вычисления прямой через две точки.
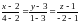
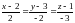
6. Для нахождения уравнения плоскости воспользуемся формулой, для нахождения плоскости, проходящей через три точки.
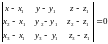
Получаем:
.
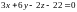7. Для нахождения высоты, нам необходимо знать направляющий вектор, в качестве которого можно взять вектор нормали и точку, через которую проходит высота.
, D(-5,-4,8).
Тогда уравнение высоты имеет вид:
.
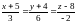8. Для нахождения точки пересечения высоты с плоскостью запишем уравнение высоты в параметрическом виде:
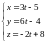
Подставляя в уравнение плоскости получим
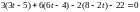
Откуда
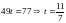
И, подставляя в параметрическое задание прямой, получаем координаты точки пересечения:
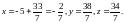
9. Длину высоты можно вычислить как расстояние между точками D и O. Получим:
.
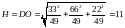