Векторы.

Определение. Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают. Обозначение: 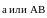. Вектор определяется его координатами . Если заданы две точки в пространстве А(х₁, y₁, z₁), B(x₂, y₂, z₂), то они определяют некоторый вектор .

Определение. Длиной (модулем) вектора называется расстояние между началом и концом вектора . Длина вектора в координатах определяется как расстояние между точками начала и конца вектора .

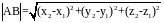Определение. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору. Вектора коллинеарны, если их координаты пропорциональны, то есть выполняется равенство: .

Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны (векторы лежат в одной плоскости).

Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.

Определение. Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые длины. Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.

Определение. Проекцией вектора на вектор (или на ось, параллельную и сонаправленную ) называют число , где  – угол между векторами и . В ортонормированном базисе координаты x, y, z вектора совпадают с его проекциями на базисные орты : .

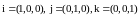Определение. Обозначим через углы между вектором и векторами соответственно. Числа 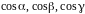называются направляющими косинусами вектора . Имеют место формулы , , Часто краткости ради вместо пишут . Аналогичные определения приняты на множестве векторов плоскости.

Определение. Скалярным произведением двух векторов и называется число, равное . Эта операция обозначается 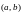или 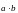. Через проекции формула запишется в виде: Если вектора заданы покоординатно то .

Используя формулу скалярного произведения векторов и можно найти выражение косинуса угла между этими векторами: . Если , то это значит, что угол между векторами больше , т.е. тупой, а если , то угол острый.

Если скалярное произведение двух векторов равно нулю, то эти векторы ортогональны. Действительно, если ни один из векторов не нулевой, то, по определению скалярного произведения, последнее может быть равно нулю только тогда, когда .

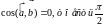Определение. Под векторным произведением 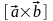векторов и понимают вектор , имеющий длину и направленный перпендикулярно к плоскости, определяемой векторами и , причем так, что векторы и и образуют правую тройку векторов.

Геометрический смысл векторного произведения: длина вектора численно равна площади параллелограмма, построенного на векторах и как на сторонах.

Физический смысл векторного произведения: если - сила, - радиус-вектор точки ее приложения, имеющий начало в точке O, то момент силы относительно точки O есть вектор, равный векторному произведению на , то есть

Определение. Смешанным произведением векторов , и назовем число, вычисляемое как:

Геометрический смысл смешанного произведения: объем параллелепипеда, построенного на векторах , и .

Если , и компланарны (лежат в одной плоскости), то .

Условие коллинеарности (вектора лежат на параллельных прямых) .

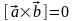Если точка M(x,y,z) делит отрезок M₁M₂ в отношении , то есть . Тогда координаты точки M вычисляются по формуле:

Пример. Даны точки A(4;–1;3), B(0;1;2), C(3;–2;5), D(1;–1;1). Найти:

1. площадь треугольника АВС;

2. высоту треугольника АВС, опущенную из вершины А на сторону ВС;

3. длину медианы AM;

4. будут ли компланарны вектора ?

5. объём пирамиды АВСD.

Решение.

а) Площадь треугольника АВС равна половине площади параллелограмма S, построенного на векторах и , т.е. . Имеем , ,

;

б)  ;    ,    ; .

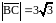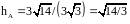c)Найдем координаты точки M. Так как АМ медиана треугольника, то точка М делит сторону BC пополам и следовательно координаты точки М можно вычислить по формуле: . Следовательно они будут равны:

Тогда длинна медианы рана: .

d) Вектора компланарны, если их смешанное произведение рано нулю. Найдем координаты векторов:

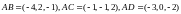
Составим определитель:

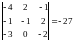
Ответ: ветора не компланарны.

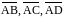e) Объём пирамиды АВСD равен объёма параллелепипеда, построенного на векторах . Имеем, , , .
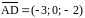