
- •Часть 1
- •Предисловие
- •Указания по выполнению и оформлению контрольной работы.
- •Тема: «Основы линейной алгебры»
- •Глава 5. Основы линейной алгебры. Стр. 130-171.
- •Основные понятия.
- •Свойства матриц.
- •Свойства определителей.
- •Системы линейных алгебраических уравнений.
- •Векторы.
- •Уравнение прямой и плоскости в пространстве.
- •Тема: «Предел функции»
- •Глава 11. Предел и непрерывность функций нескольких переменных. Стр. 275-283.
- •Предел функции.
- •Специальные пределы.
- •Тема «Производная функции и ее приложения».
- •Глава 7. Дифференциальное исчисление функции одной независимой переменной. Стр. 190-235. Задачи, приводящие к понятию производной.
- •Основные правила нахождения производной. Таблица производных
- •Вычисление производной функции.
- •Вычисление производной сложной функции.
- •Вычисление производной функции, заданной неявно.
- •Производная степенно-показательной функции.
- •Производная обратной функции.
- •Исследование функции на монотонность и экстремум, наибольшее и наименьшее значение.
- •Задачи для решения Тема: «Функция. Ее свойства и график».
- •Глава 6. Применение дифференциального исчисления к исследованию функций. Стр. 127-158.
- •Глава 5. Дифференцирование. Стр. 54-81.
- •Глава 7. Дифференциальное исчисление функции одной независимой переменной. Стр. 190-235. Общая схема исследования функции. Построение графиков
- •Тема: «Интегрирование функции».
- •Глава 8. Определенный интеграл. Стр. 177-221.
- •Глава 8. Определенный интеграл. Стр. 221-260.
- •Глава 10. Определенный интеграл. Стр. 296-325. Понятие и основные свойства неопределенного интеграла
- •Формулы интегрирования
- •Метод непосредственного интегрирования
- •Интегрирование методом замены переменной
- •Интегрирование по частям
- •Определенный интеграл и его приложения
- •Основные свойства определённого интеграла
- •Геометрический смысл определённого интеграла
- •Физический смысл определённого интеграла
- •Задания для контрольной работы.
- •Оглавление
- •Литература
Свойства определителей.
Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером.
Перестановка двух столбцов или двух строк меняет знак определителя на противоположный.
Если в определителе есть две одинаковые строки или два одинаковых столбца, то он равен нулю.
Если все элементы некоторой строки или некоторого столбца определителя равны нулю, то сам определитель равен нулю.
Умножение всех элементов некоторого столбца или строки определителя на любое число равносильно умножению определителя на это число.
Если соответствующие элементы двух строк или двух столбцов определителя пропорциональны, то определитель равен нулю.
Если каждый элемент i − ого столбца или j − ой строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в i −ом столбце или j − ой строке имеет первые слагаемые, а другой вторые слагаемые; элементы, стоящие на остальных местах у всех определителей одни и те же.
Значение определителя не изменится, если к элементам некоторой строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на любой общий множитель.
Определение.
Матрица
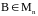 называется обратной
к матрице
называется обратной
к матрице
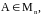 если AB =BA = ;
при этом
пишут
если AB =BA = ;
при этом
пишут
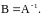 Матрица А имеет обратную только в том
случае, если она невырожденная, то есть
ее определеитель отличен от нуля.
Матрица А имеет обратную только в том
случае, если она невырожденная, то есть
ее определеитель отличен от нуля.
Если
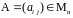 – невырожденная матрица, то
– невырожденная матрица, то
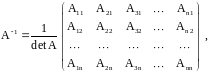
где
 алгебраические дополнения элементов
, и равно
алгебраические дополнения элементов
, и равно
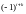 ,
умноженный на определитель матрицы,
полученной путем вычеркивания i-ой
строки и j-го столбца.
,
умноженный на определитель матрицы,
полученной путем вычеркивания i-ой
строки и j-го столбца.
Определение.
Минором
некоторого
элемента
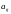 определителя п-го
порядка называется определитель п-1
- го порядка,
полученный из исходного путем вычеркивания
строки и столбца, на пересечении которых
находится выбранный элемент. Обозначается
определителя п-го
порядка называется определитель п-1
- го порядка,
полученный из исходного путем вычеркивания
строки и столбца, на пересечении которых
находится выбранный элемент. Обозначается
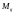 .
.
Так,
если
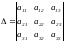 ,
то
,
то
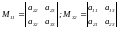 .
.
Определение.
Алгебраическим
дополнением
элемента
определителя называется его минор,
взятый со знаком «плюс», если сумма
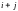 четное число,
и со знаком «минус», если эта сумма
нечетная. Обозначается
четное число,
и со знаком «минус», если эта сумма
нечетная. Обозначается
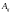 :
:
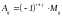 .
.
Пример.
Найти
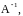 если
если
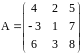 .
.
Сделать проверку.
Решение.  ,
следовательно, существует
,
следовательно, существует
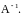
Найдем алгебраические дополнения:
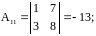
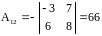 ;
; 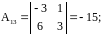
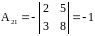 ;
;
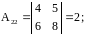
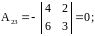

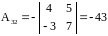 ;
; 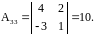
Отсюда получаем
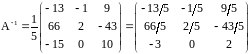 .
.
Системы линейных алгебраических уравнений.
Определение. Системой линейных алгебраических уравнений (СЛАУ) называется система уравнений вида
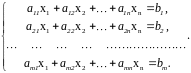
Определение.
Система
называется однородной,
если свободные члены равны нулю:
 Однородная система всегда является
совместной
она имеет решение
Однородная система всегда является
совместной
она имеет решение
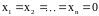 (возможно, не единственное).
(возможно, не единственное).
Матрицы
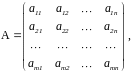
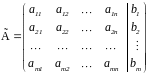 называются матрицей
системы и расширенной матрицей системы
соответственно; столбцы
называются матрицей
системы и расширенной матрицей системы
соответственно; столбцы
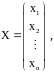
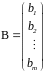
называются столбцом неизвестных и столбцом свободных членов соответственно. С учетом этих обозначений систему можно записать в матричной форме
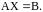
Существует три основных метода решения совместной СЛАУ
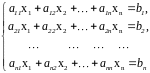
а) правило Крамера;
б) матричный способ;
в) метод Гаусса.
а) Правило Крамера.
Обозначим
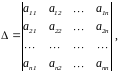
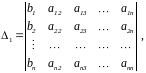
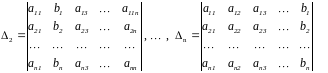
(определитель
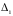 получается из
заменой i-го столбца на столбец свободных
членов). Правило Крамера состоит в том,
что при
получается из
заменой i-го столбца на столбец свободных
членов). Правило Крамера состоит в том,
что при


б)
Матричный
способ.
Система совместна при
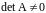 и имеет единственное решение – столбец
и имеет единственное решение – столбец
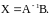
в)
Метод Гаусса.
При решении методом Гаусса расширенную
матрицу
 системы элементарными преобразованиями
приводят к треугольному виду.
системы элементарными преобразованиями
приводят к треугольному виду.
Пример. Решить систему

а) по правилу Крамера;
б) матричным способом;
в) методом Гаусса.
Решение. а) Имеем
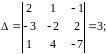

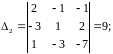
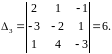
Отсюда находим

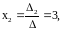

б)

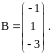
Найдем 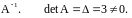
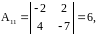
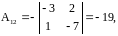
 ;
;
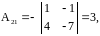
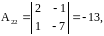
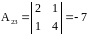 ;
;
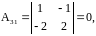
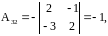
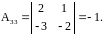
Поэтому
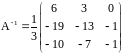 .
.
Отсюда находим
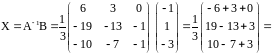
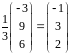 .
.
Итак,
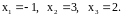
в) Решим систему методом Гаусса:
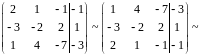
Ко второй строке прибавим первую, умноженную на три; из третьей строки вычтем вторую, умноженную на 2. Получим:
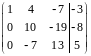
Третью строку умножим на 10, вторую на 7 и сложим их:
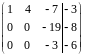 .
.
Последней матрице, имеющей треугольный вид (если исключить столбец свободных членов), соответствует следующая СЛАУ, равносильная исходной системе:
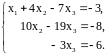
Из
последнего уравнения находим
 ,
подставив его во второе уравнение,
найдем
,
подставив его во второе уравнение,
найдем
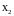 и, наконец, подставив найденные
и
в первое уравнение, найдем
и, наконец, подставив найденные
и
в первое уравнение, найдем
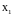 :
:
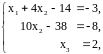
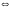
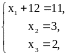
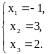
Следует иметь в виду, что при решении СЛАУ методом Гаусса перестановка столбцов приводит к перенумерации неизвестных.
Тема: Элементы векторной алгебры и аналитической геометрии.
Вопросы:
Понятие вектора.
Свойства векторов, линейные операции над векторами.
Понятие скалярного, векторного и смешенного произведения их свойства и правила вычисления.
Приложения скалярного, векторного и смешанного произведений.
Прямая. Способы задания прямой на плоскости и в пространстве.
Плоскость. Способы задания плоскости.
Взаимное расположение прямых и плоскостей.
В результате изучения темы слушатели должны уметь:
совершать операции с векторами,
определять взаимное расположение прямых и плоскостей,
решать геометрические задачи.
Эти вопросы рассмотрены в [1],[3],[5],[8] и там же приведены примеры решений типовых задач.
[1] Глава 3. Аналитическая геометрия на плоскости. Стр. 34-68.
Глава 9. Аналитическая геометрия в пространстве. Стр. 222-258.
[2] Глава 3. Аналитическая геометрия на плоскости. Стр. 18-35.
Глава 10. Аналитическая геометрия в пространстве. Стр. 152-178.
[3] Глава 2. Элементы векторной алгебры. Стр 31-47.
Глава 3. Аналитическая геометрия на плоскости. Стр.48-75.
Глава 4. Аналитическая геометрия в пространстве. Стр. 76-96.
[5] Глава 1. Аналитическая геометрия на плоскости. Стр. 6-53.
Глава 2. Элементы векторной алгебры. Стр. 54-64.
Глава 3. Аналитическая геометрия в пространстве. Стр. 65-86.
