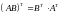Тема: «Основы линейной алгебры»
Вопросы:
Понятие матрицы.
Виды матриц.
Понятие определителя и его свойства.
Правила вычисления определителей.
Системы линейных уравнений.
Метод Крамера.
Метод Гаусса.
Метод обратной матрицы.
В результате изучения темы слушатели должны уметь:
совершать операции с матрицами,
вычислять определители,
решать системы линейных уравнений.
Эти вопросы рассмотрены в [1],[3],[5],[8] и в [2],[3],[5],[8] приведены примеры решений типовых задач.
[1] Глава 10. Элементы высшей алгебры. Стр. 259-274.
[2] Глава 7. Элементы высшей алгебры. Стр. 123-129.
[3] Глава 1. Элементы линейной алгебры. Стр. 10-30.
[5] Глава 4. Определители и матрицы. Стр. 87-129.
Глава 5. Основы линейной алгебры. Стр. 130-171.
Дадим краткий обзор понятий, которые необходимы для понимания материала и решения практических задач.
Основные понятия.
Определение.
Матрицей
порядка
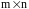называется прямоугольная таблица чисел
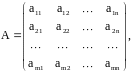
состоящая
из m строк и n столбцов, рассматриваемая
как единый объект, над которым могут
производиться определенные алгебраические
действия (например, сложение, умножение).
Элементы матрицы обозначают через
,
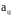где,
,
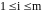1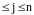
.
Здесь aij - элементы матрицы. Каждый элемент имеет два индекса, первый обозначает номер строки, а второй номер столбца.
Определение. Матрица называется квадратной, если у нее количество строк и столбцов одинаковое.
Элементы
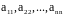образуют главную диагональ,
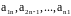- побочную.
Определение. Определителем квадратной матрицы называется число, равное сумме произведений этой матрицы, взятых по одному из каждой строки и каждого столбца.
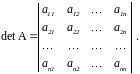
Определитель второго порядка вычисляется по формуле
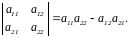
Определитель третьего порядка вычисляется по формуле
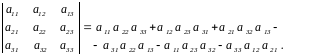
Для
вычисления определителя третьего
порядка лучше пользоваться правилом
Саррюса (треугольника) или правилом
«3
5».
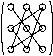
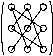
Схематически их можно изобразить на
рисунках:
+ –
а б Рис. 1 Элементы перемножаются и потом суммируются, причем слагаемые с рис. а берутся со знаком «+», а с рис. б – со знаком «-» |
Рис. 2 Элементы перемножаются и потом суммируются, причем произведения «параллельные» главной диагонали берутся со знаком «+», а параллельные побочной – со знаком «-» |
Пример. Вычислить определитель
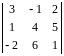
методом «треугольника”;
Решение. По правилу Саррюса имеем
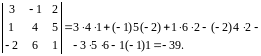
Свойства матриц.
Суммой
двух матриц
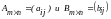называется
матрица
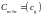такая, что
(
).
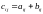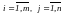Замечание: операция сложения матриц вводится только для матриц одинаковых размеров.
Аналогично определяется разность матриц.
Замечание:
разность матриц А–В
можно определить так:
.
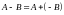Произведением
матрицы
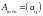на число k
называется матрица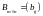
такая, что
(
).
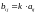Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:
;
;
;
;
;
;
;
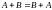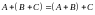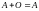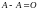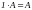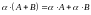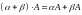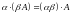,где А, В, С – матрицы,
и
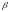– числа.
Умножение матриц обладает следующими свойствами:
;
;
;
,
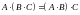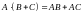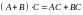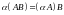Определение. Элементарными преобразованиями матриц являются:
перестановка местами двух параллельных рядов матрицы;
умножение всех элементов ряда матрицы на число, отличное от нуля;
прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.
Определение. Операцией транспонирования называется операция, при которой строки матрицы становятся столбцами, а столбцы – строками.
Для операции транспонирования верны свойства:
;
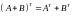