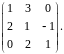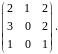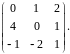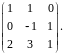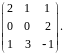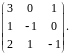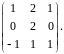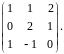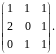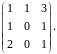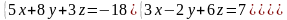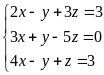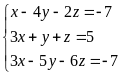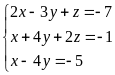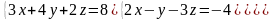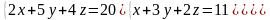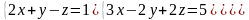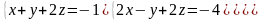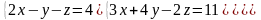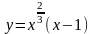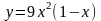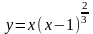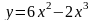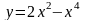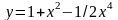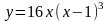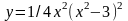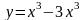- •Часть 1
- •Предисловие
- •Указания по выполнению и оформлению контрольной работы.
- •Тема: «Основы линейной алгебры»
- •Глава 5. Основы линейной алгебры. Стр. 130-171.
- •Основные понятия.
- •Свойства матриц.
- •Свойства определителей.
- •Системы линейных алгебраических уравнений.
- •Векторы.
- •Уравнение прямой и плоскости в пространстве.
- •Тема: «Предел функции»
- •Глава 11. Предел и непрерывность функций нескольких переменных. Стр. 275-283.
- •Предел функции.
- •Специальные пределы.
- •Тема «Производная функции и ее приложения».
- •Глава 7. Дифференциальное исчисление функции одной независимой переменной. Стр. 190-235. Задачи, приводящие к понятию производной.
- •Основные правила нахождения производной. Таблица производных
- •Вычисление производной функции.
- •Вычисление производной сложной функции.
- •Вычисление производной функции, заданной неявно.
- •Производная степенно-показательной функции.
- •Производная обратной функции.
- •Исследование функции на монотонность и экстремум, наибольшее и наименьшее значение.
- •Задачи для решения Тема: «Функция. Ее свойства и график».
- •Глава 6. Применение дифференциального исчисления к исследованию функций. Стр. 127-158.
- •Глава 5. Дифференцирование. Стр. 54-81.
- •Глава 7. Дифференциальное исчисление функции одной независимой переменной. Стр. 190-235. Общая схема исследования функции. Построение графиков
- •Тема: «Интегрирование функции».
- •Глава 8. Определенный интеграл. Стр. 177-221.
- •Глава 8. Определенный интеграл. Стр. 221-260.
- •Глава 10. Определенный интеграл. Стр. 296-325. Понятие и основные свойства неопределенного интеграла
- •Формулы интегрирования
- •Метод непосредственного интегрирования
- •Интегрирование методом замены переменной
- •Интегрирование по частям
- •Определенный интеграл и его приложения
- •Основные свойства определённого интеграла
- •Геометрический смысл определённого интеграла
- •Физический смысл определённого интеграла
- •Задания для контрольной работы.
- •Оглавление
- •Литература
Задания для контрольной работы.
Найти определитель.
Решить систему тремя способами: Крамера и методом обратной матрицы.
Даны вершины тетраэдра A, B, C, D.
Найти:
длину ребра AB;
угол между ребрами AB и AD;
угол между ребром AD и плоскостью ABC;
объем тетраэдра ABCD;
уравнение ребра AB;
уравнение плоскости ABC;
уравнение высоты, опущенной из D на ABC;
проекцию точки D на ABC;
длину высоты DO.
А(1; 2; 1), В(2; -3; 4), С(-4; 5; 1), D(-1; 2; -3).
А(-4; -3; -2), В(4; 5; 1), С(-2; 2; 5), D(6; -1; 2).
А(1; -2; 1), В(3; 1; 4), С(2; 7; 6), D(-2; 3; -5).
А(4; 1; 5), В(1; -1; -1), С(3; 3; 3), D(5; -5; -2).
А(0; 3; 4), В(5; 7; 6), С(-3; 0; 6), D(-1; -1; -1).
А(3; 2; 2), В(-4; -3; -2), С(5; 5; 5), D(6; 0; 3).
А(6; -2; 1), В(4; 4; 4), С(-2; 4; -3), D(-3; 2; -6).
А(5; 3; 2), В(2; -2; -2), С(7; -6; 5), D(4; -3; 4).
А(4; 3; 2), В(3; 1; 4), С(1; -2; -1), D(3; -5; 0).
А(5; 0; 4), В(1; -2; -4), С(2; -1; -3), D(-5; 1; 6).
Вычислить пределы функции.
 ,
,
 ,
,
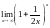
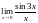 ,
,
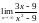 ,
,

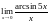 ,
,
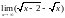 ,
,
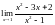
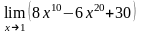 ,
,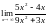 ,
,
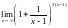
,
 ,
,
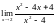
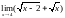 ,
,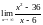 ,
,
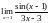 ,
,
 ,
,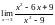
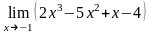 ,
,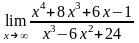 ,
,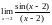
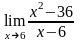 ,
,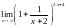 ,
,
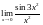 ,
,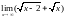 ,
,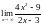
Вычислить производную.

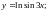
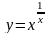 ;
;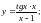
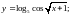
 ;
;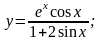
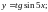
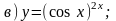
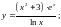
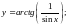
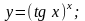
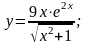
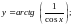

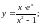
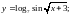

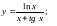
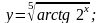
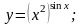
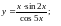
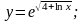
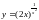 ;
;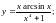
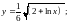
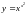 ;
;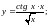
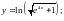
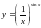 ;
;
Исследовать функцию и построить ее график.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислить интеграл.
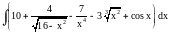 ,
,
 ,
,
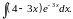
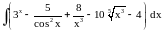 ,
,
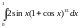 ,
,
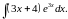
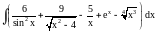 ,
,
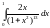 ,
,
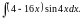
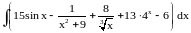 ,
,
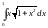 ,
,
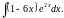
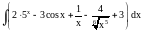 ,
,
 ,
,
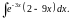
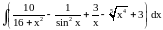 ,
,
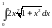 ,
,
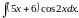
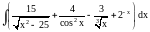 ,
,
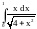 ,
,
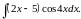
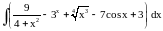 ,
,
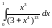 ,
,
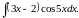
 ,
,
 ,
,
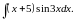
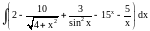 ,
,
 ,
,
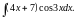
-
Найти объем тела вращения, полученного в результате вращения кривой
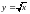 вокруг оси ох, и ограниченного
плоскостями x=1,
x=2.
вокруг оси ох, и ограниченного
плоскостями x=1,
x=2.
Тело движется вдоль оси Ox и его скорость изменяется по закону
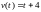 .
Найти путь, пройденный за первые 4
секунды движения.
.
Найти путь, пройденный за первые 4
секунды движения.
-
Найти объем тела вращения, полученного в результате вращения кривой
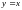 вокруг оси ох, и ограниченного
плоскостями x=1,
x=2.
вокруг оси ох, и ограниченного
плоскостями x=1,
x=2.
Тело движется вдоль оси Ox и его скорость изменяется по закону
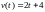 .
Найти путь, пройденный за первые 4
секунды движения.
.
Найти путь, пройденный за первые 4
секунды движения.
-
Найти объем тела вращения, полученного в результате вращения кривой
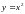 вокруг оси ох, и ограниченного
плоскостями x=1,
x=2.
вокруг оси ох, и ограниченного
плоскостями x=1,
x=2.
Тело движется вдоль оси Ox и его скорость изменяется по закону
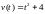 .
Найти путь, пройденный за первые 5
секунд движения.
.
Найти путь, пройденный за первые 5
секунд движения.
-
Найти объем тела вращения, полученного в результате вращения кривой вокруг оси ох, и ограниченного плоскостями x=1, x=3.
Тело движется вдоль оси Ox и его скорость изменяется по закону
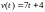 .
Найти путь, пройденный за первые 3
секунды движения.
.
Найти путь, пройденный за первые 3
секунды движения.
-
Найти площадь фигуры, ограниченной линиями y = -x2 + 4, y =3.
Тело движется вдоль оси Ox и его скорость изменяется по закону
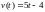 .
Найти путь, пройденный за промежуток
времени от 1 до 4 секунд.
.
Найти путь, пройденный за промежуток
времени от 1 до 4 секунд.
-
Найти объем тела вращения, полученного в результате вращения кривой
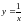 вокруг оси ох, и ограниченного
плоскостями x=1,
x=2.
вокруг оси ох, и ограниченного
плоскостями x=1,
x=2.
Тело движется вдоль оси Ox и его скорость изменяется по закону
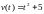 .
Найти путь, пройденный за первые 4
секунды движения.
.
Найти путь, пройденный за первые 4
секунды движения.
-
Найти площадь фигуры, ограниченной линиями y = cosx, y = 0,
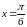 ,
,
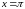 .
.Тело движется вдоль оси Ox и его скорость изменяется по закону
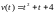 .
Найти путь, пройденный за первые 4
секунды движения.
.
Найти путь, пройденный за первые 4
секунды движения.
-
Вычислить площадь фигуры, ограниченной линиями: y = sinx, y = 0,
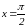 ,
,
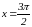
Тело движется вдоль оси Ox и его скорость изменяется по закону
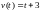 .
Найти путь, пройденный за первые 5
секунды движения.
.
Найти путь, пройденный за первые 5
секунды движения.
-
Вычислить площадь фигуры, ограниченной линиями:
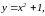
y = 0, х =-1, х = 3.
Тело движется вдоль оси Ox и его скорость изменяется по закону
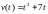 .
Найти путь, пройденный за первые 4
секунды движения.
.
Найти путь, пройденный за первые 4
секунды движения.
Найти объем тела вращения, полученного в результате вращения кривой
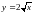 вокруг оси ох, и ограниченного
плоскостями x=1,
x=2.
вокруг оси ох, и ограниченного
плоскостями x=1,
x=2.
Тело движется вдоль оси Ox и его скорость изменяется по закону . Найти путь, пройденный за первые 4 секунды движения.
Правила оформления титульного листа контрольной работы
МИНИСТЕРСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ ПО ДЕЛАМ ГРАЖДАНСКОЙ ОБОРОНЫ, ЧРЕЗВЫЧАЙНЫМ СИТУАЦИЯМ И ЛИКВИДАЦИИ ПОСЛЕДСТВИЙ СТИХИЙНЫХ БЕДСТВИЙ
Федеральное государственное Бюджетное Образовательное Учреждение Высшего Профессионального Образования
Воронежский институт Государственной противопожарной службы
Кафедра прикладной математики и инженерной графики
Контрольная работа по дисциплине «Высшая математика»
Вариант № 0
Выполнил слушатель 11 учебной группы ФЗО (6 лет обучения ВПО) ст. л-т внутренней службы Иванов Петр Иванович
Домашний адрес: 394000, г. Воронеж Ул. Никитинская, д.5 кв. 12.
ВОРОНЕЖ 2013
|