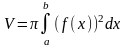- •Часть 1
- •Предисловие
- •Указания по выполнению и оформлению контрольной работы.
- •Тема: «Основы линейной алгебры»
- •Глава 5. Основы линейной алгебры. Стр. 130-171.
- •Основные понятия.
- •Свойства матриц.
- •Свойства определителей.
- •Системы линейных алгебраических уравнений.
- •Векторы.
- •Уравнение прямой и плоскости в пространстве.
- •Тема: «Предел функции»
- •Глава 11. Предел и непрерывность функций нескольких переменных. Стр. 275-283.
- •Предел функции.
- •Специальные пределы.
- •Тема «Производная функции и ее приложения».
- •Глава 7. Дифференциальное исчисление функции одной независимой переменной. Стр. 190-235. Задачи, приводящие к понятию производной.
- •Основные правила нахождения производной. Таблица производных
- •Вычисление производной функции.
- •Вычисление производной сложной функции.
- •Вычисление производной функции, заданной неявно.
- •Производная степенно-показательной функции.
- •Производная обратной функции.
- •Исследование функции на монотонность и экстремум, наибольшее и наименьшее значение.
- •Задачи для решения Тема: «Функция. Ее свойства и график».
- •Глава 6. Применение дифференциального исчисления к исследованию функций. Стр. 127-158.
- •Глава 5. Дифференцирование. Стр. 54-81.
- •Глава 7. Дифференциальное исчисление функции одной независимой переменной. Стр. 190-235. Общая схема исследования функции. Построение графиков
- •Тема: «Интегрирование функции».
- •Глава 8. Определенный интеграл. Стр. 177-221.
- •Глава 8. Определенный интеграл. Стр. 221-260.
- •Глава 10. Определенный интеграл. Стр. 296-325. Понятие и основные свойства неопределенного интеграла
- •Формулы интегрирования
- •Метод непосредственного интегрирования
- •Интегрирование методом замены переменной
- •Интегрирование по частям
- •Определенный интеграл и его приложения
- •Основные свойства определённого интеграла
- •Геометрический смысл определённого интеграла
- •Физический смысл определённого интеграла
- •Задания для контрольной работы.
- •Оглавление
- •Литература
Основные свойства определённого интеграла
Определенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определенных интегралов от слагаемых функций:
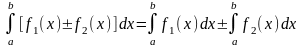 .
.Постоянный множитель можно выносить за знак определенного интеграла:
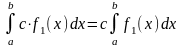 .
.При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:
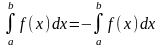 .
.Определенный интеграл с одинаковыми пределами равен нулю:
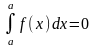 .
.Отрезок интегрирования можно разбивать на части:
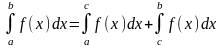 .
.Формула Ньютона-Лейбница: Если F(x) – первообразная функция для непрерывной функции y=f(x), т.е. F'(x) = f(x), то имеет место формула:
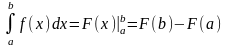 .
.Замена переменных:
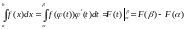 ,
где
,
где
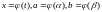 .
.Интегрирование по частям: Если u=u(x), v=v(x) – функции, имеющие непрерывные производные на некотором промежутке, то справедлива формула интегрирования по частям:
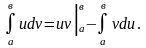
Геометрический смысл определённого интеграла
|
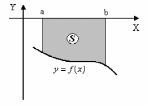
Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [a; b] функции f(x), осью ОХ и прямыми х=а и х=в:
|
|
Площадь криволинейной трапеции, ограниченной графиком непрерывной отрицательной на промежутке [a; b] функции f(x), осью ОХ и прямыми х=а и х=в:
|
|
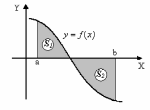
Если функция изменяет знак на промежутке [a; b], то
|
|
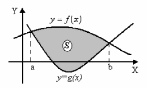
Площадь фигуры,
ограниченной двумя пересекающимися
кривыми y=f(x)
и y=g(x)
таких, что f(x)
|
|
Объём тела,
полученного в результате вращения
вокруг оси ОХ криволинейной трапеции,
ограниченной графиком непрерывной
и неотрицательной функции y=f(x)
на отрезке [a;
b]:
|
Физический смысл определённого интеграла
При
прямолинейном движении
перемещение
s
численно равно определенному интегралу
от функции зависимости скорости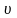 от времени t:
от времени t:
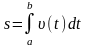 .
.
Пример.
Вычислить
площадь фигуры, ограниченной линиями: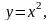 y
= 0, х = 2, х = 3.
y
= 0, х = 2, х = 3.
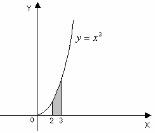
Решение.
Построим графики функций х = 2, х = 3.
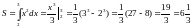 .
.
Пример. Определить объём тела, которое получается в результате вращения вокруг оси Ох параболы y2 = 4х и прямой х =3.
Решение.
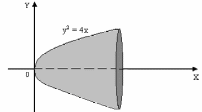
Так как данная парабола (с вершиной в начале координат) вращается вокруг оси Ох и ограничена прямой х = 3, то для вычисления объёма воспользуемся следующей формулой:
Vх
=
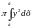 .
Таким образом, получим:
.
Таким образом, получим:
Vх
=
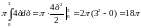
Таблица вариантов заданий
Предпоследняя цифра зачетной книжки |
|
Последняя цифра номера зачетной книжки |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
10,18,26, 34,42, 60,68, 76 |
1,14,27, 40,43, 56,69, 72 |
10,17,24, 31,48, 55,62, 79 |
1,15,29, 33,47, 51,65, 75 |
10,16,22, 38,44, 60,66, 72 |
1,16,21, 36,41, 56,61, 76 |
1,11,21, 31,41, 51,61, 71 |
1,12,23, 34,45, 56,67, 78 |
10,19,28,37,46, 55,64, 73 |
1,13,25, 37,49, 51,63, 75 |
|
|
|
2,14,26, 38,50, 52,64, 76 |
2,15,28, 31,44, 57,70, 73 |
9,16,23, 40,47, 54,61, 78 |
2,16,30, 34,48, 52,66, 80 |
9,15,21, 37,43, 59,65, 71 |
2,17,22, 37,42, 57,62, 77 |
2,12,22, 32,42, 52,62, 72 |
2,13,24, 35,46, 57,68, 79 |
9,18,27, 36,45, 54,63, 72 |
9,17,25, 33,41, 59,67, 75 |
|
|
|
3,15,27, 39,41, 53,65, 77 |
8,16,24, 32,50, 58,66, 74 |
8,15,22, 39,46, 53,70, 77 |
3,17,21, 35,49, 53,67, 71 |
8,14,30, 36,42, 58,64, 80 |
3,18,23, 38,43, 58,63, 78 |
3,13,23, 33,43, 53,63, 73 |
3,14,25, 36,47, 58,69, 80 |
8,17,26, 35,44, 53,62, 71 |
3,16,29, 32,45, 58,61, 74 |
|
|
|
4,16,28, 40,42, 54,66, 78 |
7,15,23, 31,49, 57,65, 73 |
4,17,30, 33,46, 59,62, 75 |
4,18,22, 36,50, 54,68, 72 |
7,13,29, 35,41, 57,63, 79 |
4,19,24, 39,44, 59,64, 79 |
4,14,24, 34,44, 54,64, 74 |
4,15,26, 37,48, 59,61, 72 |
7,16,25, 34,43, 52,61, 80 |
7,14,21, 38,45, 52,70, 77 |
|
|
|
5,17,29, 31,43, 55,67, 79 |
6,14,22, 40,48, 56,64, 72 |
5,18,21, 34,47, 60,63, 76 |
6,13,30, 37,44, 51,68, 75 |
6,12,28, 34,50, 56,62, 78 |
5,20,25, 40,45, 60,65, 80 |
5,15,25, 35,45, 55,65, 75 |
5,16,27, 38,49, 51,62, 73 |
6,15,24, 33,42, 51,70, 79, |
5,19,23, 37,41, 55,69, 73 |
|
|
|
6,18,30, 32,44, 56,68, 80 |
5,13,21, 39,47, 55,63, 71 |
6,19,22, 35,48, 51,64, 77 |
5,12,29, 36,43, 60,67, 74 |
8,20,24, 38,42, 56,70, 74 |
6,11,26, 31,46, 51,66, 71 |
7,17,27, 37,47, 57,67, 77 |
5,14,23, 32,41, 60,69, 78 |
1,17,28, 39,41, 52,63, 74 |
5,11,27, 33,49, 55,61, 77 |
|
|
|
7,19,21, 33,45, 57,69, 71 |
4,12,30, 38,46, 54,62, 80 |
7,20,23, 36,49, 52,65, 78 |
4,11,28, 35,42, 59,66, 73 |
7,11,25, 39,43, 57,61, 75 |
4,20,26, 32,48, 54,70, 76 |
7,12,27, 32,47, 52,67, 72 |
8,18,28, 38,48, 58,68, 78 |
2,19,21, 32,43, 54,65, 76 |
3,12,21, 40,49, 58,67, 76 |
|
|
|
8,20,22, 34,46, 58,70, 72 |
3,11,29, 37,45, 53,61, 79 |
8,11,24, 37,50, 53,66, 80 |
3,20,27, 34,41, 58,65, 72 |
8, 12,26, 40,44, 58,62, 76 |
3,19,25, 31,47, 53,69, 75 |
8,13,28, 33,48, 53,68, 73 |
10,20, 30,40, 50,60, 70,80 |
9, 13,27, 31,45, 59,63, 77 |
6,16,26, 36,46, 56,66, 76 |
|
|
|
9,11,23, 35,47, 59,61, 73 |
2,20,28, 36,44, 52,70, 78 |
5,12,25, 38,41, 54,67, 80 |
2,19,26, 33,50, 57,64, 71 |
10,12,23, 34,45, 56,62, 77 |
2,18,24, 40,46, 52,68, 74 |
9,14,29, 34,49, 54,69, 74, |
6,19,29, 39,49, 59,69, 79, |
1,20,29, 38,47, 56,65, 74 |
10,14,28, 32,46, 60,64, 78 |
|
|
|
10,12,24, 36,48, 60,62, 74 |
1,19,27, 35,43, 51,69, 77 |
10,13,26, 39,42, 55,68, 71 |
1,18,25, 32,49, 56,63, 80 |
2,11,30, 39,48, 57,66, 75 |
1,17,23, 39,45, 51,67, 73 |
10,15,30, 35,50, 55,70, 75 |
9,11,22, 33,44, 55,66, 77 |
4,13,22, 31,50, 59,68, 79 |
7,18,29, 31,42, 53,64, 75 |
|


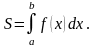

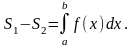
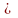 g(x)
для любого х
g(x)
для любого х ,
где а и b
– абсциссы точек пересечения графиков
функций:
,
где а и b
– абсциссы точек пересечения графиков
функций:
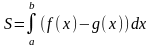 .
.