
- •Часть 1
- •Предисловие
- •Указания по выполнению и оформлению контрольной работы.
- •Тема: «Основы линейной алгебры»
- •Глава 5. Основы линейной алгебры. Стр. 130-171.
- •Основные понятия.
- •Свойства матриц.
- •Свойства определителей.
- •Системы линейных алгебраических уравнений.
- •Векторы.
- •Уравнение прямой и плоскости в пространстве.
- •Тема: «Предел функции»
- •Глава 11. Предел и непрерывность функций нескольких переменных. Стр. 275-283.
- •Предел функции.
- •Специальные пределы.
- •Тема «Производная функции и ее приложения».
- •Глава 7. Дифференциальное исчисление функции одной независимой переменной. Стр. 190-235. Задачи, приводящие к понятию производной.
- •Основные правила нахождения производной. Таблица производных
- •Вычисление производной функции.
- •Вычисление производной сложной функции.
- •Вычисление производной функции, заданной неявно.
- •Производная степенно-показательной функции.
- •Производная обратной функции.
- •Исследование функции на монотонность и экстремум, наибольшее и наименьшее значение.
- •Задачи для решения Тема: «Функция. Ее свойства и график».
- •Глава 6. Применение дифференциального исчисления к исследованию функций. Стр. 127-158.
- •Глава 5. Дифференцирование. Стр. 54-81.
- •Глава 7. Дифференциальное исчисление функции одной независимой переменной. Стр. 190-235. Общая схема исследования функции. Построение графиков
- •Тема: «Интегрирование функции».
- •Глава 8. Определенный интеграл. Стр. 177-221.
- •Глава 8. Определенный интеграл. Стр. 221-260.
- •Глава 10. Определенный интеграл. Стр. 296-325. Понятие и основные свойства неопределенного интеграла
- •Формулы интегрирования
- •Метод непосредственного интегрирования
- •Интегрирование методом замены переменной
- •Интегрирование по частям
- •Определенный интеграл и его приложения
- •Основные свойства определённого интеграла
- •Геометрический смысл определённого интеграла
- •Физический смысл определённого интеграла
- •Задания для контрольной работы.
- •Оглавление
- •Литература
Тема: «Интегрирование функции».
Вопросы:
Понятие первообразной и неопределенного интеграла.
Свойства интегралов.
Основные методы интегрирования.
Определенный интеграл.
Приложения определенного интеграла.
В результате изучения темы слушатели должны уметь:
Вычислять неопределенные и определенные интегралы.
Решать задачи, сводящиеся к нахождению интеграла.
Эти вопросы рассмотрены в [1],[3],[5] и в [2],[3],[5] приведены примеры решений типовых задач.
[1] Глава 7. Неопределенный интеграл. Стр. 159-176.
Глава 8. Определенный интеграл. Стр. 177-221.
[2] Глава 6. Интегрирование. Стр.82-122.
[3] Глава 7. Неопределенный интеграл. Стр. 193-220.
Глава 8. Определенный интеграл. Стр. 221-260.
[5] Глава 9. Неопределенный интеграл. Стр. 256-295.
Глава 10. Определенный интеграл. Стр. 296-325. Понятие и основные свойства неопределенного интеграла
Часто приходится
решать задачу, обратную дифференцированию:
дана функция
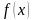 ,
требуется найти функцию
,
требуется найти функцию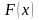 такую, что
такую, что
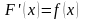 .
.
Определение.
Функция
,
называется первообразной
для функции
в промежутке
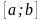 ,
если в любой точке этого промежутка ее
производная равна
т.е.:
,
,
если в любой точке этого промежутка ее
производная равна
т.е.:
,
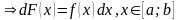 .
.
Так
как
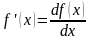 ,
отсюда дифференциал функции:
,
отсюда дифференциал функции:
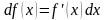
Определение. Отыскание первообразной есть операция, обратная дифференцированию и называется интегрированием.
Определение.
Совокупность
всех первообразных функции
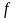 ,
определенных на некотором промежутке
,
называется неопределенным
интегралом
от функции
на промежутке
и обозначается:
,
определенных на некотором промежутке
,
называется неопределенным
интегралом
от функции
на промежутке
и обозначается:
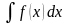
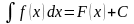
где
- подынтегральная функция,
 - подынтегральное выражение,
- переменная интегрирования, С –
постоянная интегрирования.
- подынтегральное выражение,
- переменная интегрирования, С –
постоянная интегрирования.
Основные свойства неопределенного интеграла.
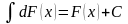 ,
,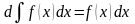 ,
,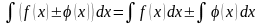 ,
,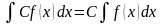 ,
где
,
где
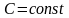 .
.
Формулы интегрирования
1.
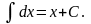
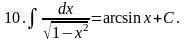
2.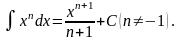
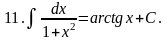
3.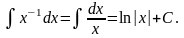 12.
12.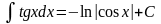 .
.
4.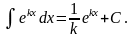 13.
13.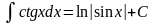 .
.
5.
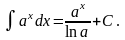 14.
14. .
.
6.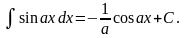 15.
15.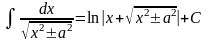 .
.
 16.
16. .
.
 17.
17.
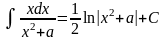
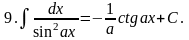 18.
18.
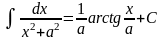
Метод непосредственного интегрирования
Используются основные свойства определенного интеграла:
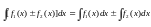 .
.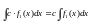 .
.
Пример.
Вычислить
интеграл:
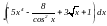 .
.
Решение.
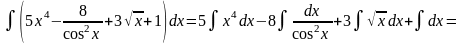
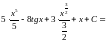
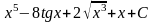 .
.
Интегрирование методом замены переменной
Сущность метода: путем введения новой переменной интегрирования заданный интеграл сводится к новому, который легко вычисляется по какой-либо из основных формул интегрирования.
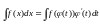
Пример.
Вычислить
интеграл:
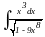 .
.
Решение.
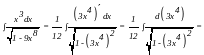
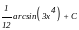 .
.
Пример.
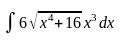
Решение.
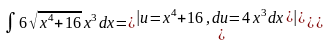
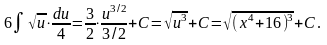
Пример.
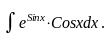
Решение.
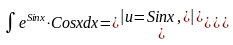
Интегрирование по частям
Интегрирование
по частям основано на формуле
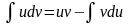 ;
;
Основные классы функций, для применения интегрирования по частям:
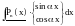
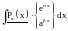
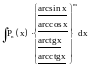
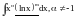
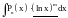
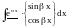
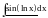
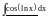
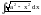
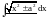
Пример.
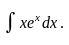
Решение.

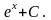

Пример.
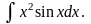
Решение.
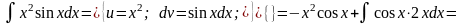
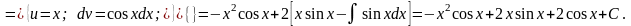
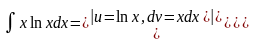
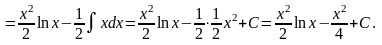
Пример.
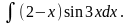
Решение.
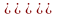
Часто при решении помогает такая формула:

Определенный интеграл и его приложения
Определение. Интегральной суммой для функции f(x) на отрезке [a;b] называется сумма вида:
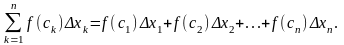
Определение.
Определенным
интегралом
от функции
f(x) на отрезке [a;b] называется предел
интегральной суммы при условии, что
длина наибольшего из элементарных
отрезков стремится к нулю: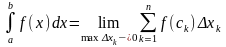 .
.
