4.5. Другие способы определения усилий в фермах

 

Рассмотренные выше способы определения усилий (способ вырезания узлов и способ сечений) можно отнести к основным способам расчета ферм.

Однако в некоторых случаях ни один из них не приводит к желаемому результату, и тогда приходится прибегать к другим способам расчета. Рассмотрим некоторые из них.

 

4.5.1. Способ замкнутого сечения

 

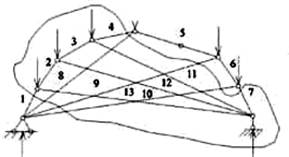
Пусть требуется определить усилия в стержнях фермы Шухова (рис.4.34,а). Применение способа вырезания узлов нецелесообразно, так как здесь нет узлов, в которых сходились бы только два стержня с неизвестными усилиями, и нельзя использовать способ проекций, так как невозможно провести сечение через три стержня.

а) б)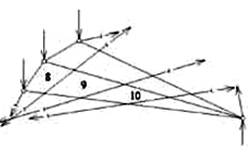

Рис.4.34

Проведем замкнутое сечение так, чтобы три стержня (1, 4, 7) пересекались по одному разу, а стержни 8, 9, 10 – по два раза. Рассмотрим равновесие отсеченной части фермы внутри замкнутого контура (рис.4.34,б). Усилия в стержнях 8, 9, 10, перерезанных замкнутым сечением дважды, уравновешиваются. А усилия в стержнях 1, 4, 7 можно определить способом моментной точки, после чего легко определить усилия в остальных стержнях фермы.

4.5.2. Способ совместных сечений

Применение этого способа приводит к системе двух уравнений с двумя неизвестными. Способ используется в тех случаях, когда удается провести два сечения таким образом, что каждое из них содержит четыре неизвестных, причем какие-то два неизвестных усилия повторяются в обоих сечениях. Ниже будет рассмотрен пример определения усилий способом совместных сечений.

4.5.3. Графический способ определения усилий

(диаграмма Максвелла-Кремоны)

Этот способ основан на графическом приеме разложения силы на два направления и состоит в следующем: буквами или цифрами обозначают полигоны (поля), т.е. площади, ограниченные со всех сторон стержнями или примыкающие к наружному контуру фермы и отделенные друг от друга внешними силами, включая опорные реакции (рис.4.35).

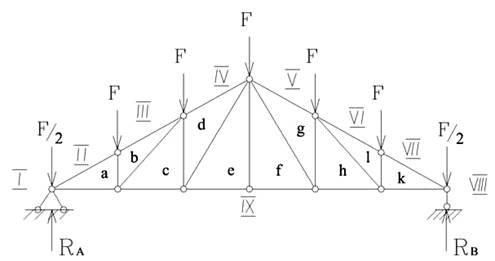
Рис.4.35

В результате каждое внутреннее усилие и каждая внешняя сила обозначаются двумя значками, соответствующими названиям тех полигонов, границей которых эта внешняя сила или усилие является. Строят многоугольник сил на внешних силах, включая опорные реакции. Каждая из сил этого многоугольника обозначается буквами или цифрами, поставленными на ее концах, при этом сохраняется направление сил.

Затем выбирают узел, в котором сходятся два стержня. Приложенную в узле силу раскладывают по направлениям этих стержней, в результате чего определяют значения и направления действующих в них усилий (направления определяют растяжение–сжатие). Разложить силы на две составляющие можно построением силового треугольника. Такой треугольник должен быть замкнут, так как узел, для которого он строится, находится в равновесии. Если к узлу приложены две и более известных сил, то строят многоугольник равновесия известных и неизвестных сил. После этого переходят к следующему узлу и для него проводят аналогичные построения. Таким образом, определяют усилия во всех стержнях фермы.