3.2. Сила Лоренца

Вернемся теперь к действию магнитного поля на ток. Так как электрический ток есть напра­в­лен­ное движение заря­женных частиц (электронов или ионов), то отсюда следует, что на дви­жу­щийся заряд в магнитном поле действует сила. Получим вы­ражение для этой силы.

На проводник длиной / с током / действует сила, определяемая формулой (4):

(11)

Произведение Il может быть выражено через заряд q, скорость υ направленного движения и полное число N носителей по формуле:

,

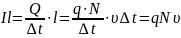где Q – полный заряд, прошедший через поперечное сечение проводника за время Δt.

При такой замене угол α в (11) можно рассматривать как угол между вектором и скоростью υ носителей, так как их направлен­ное движение происходит вдоль провода. Таким образом, для действующей на все N носителей силы из (11) получаем

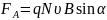(12)

Разделив (12) на N, найдем силу F, действующую на одну частицу с зарядом q, движущуюся со скоростью υ под углом α к магнитному полю:

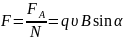. (13)

Эта сила перпендикулярна скорости заряда 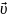и индукции магнит­ного поля , а ее модуль пропорционален синусу угла между этими векторами. Именно таким свойством обладает векторное произведе­ние. Поэтому выражение для силы F можно записать с помощью век­торного произведения:

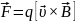. (14)

Порядок сомножителей в векторном произведении в (14) выбран так, чтобы обеспечить соответствие с правилом левой руки, опреде­ляющим направление действующей на ток силы Ампера.

Если имеется еще и электрическое поле, то полная действующая на заряд q сила F равна

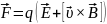(15)

Выражение (15) впервые было получено X. А. Лоренцем, родоначаль­ником электронной теории строения вещества. Поэтому силу, действу­ющую на заряд в электрическом поле, называют силой Лоренца.

Первое слагаемое в выражении (15) для силы Лоренца определяет силу, действующую на заряд со стороны электрического поля. Эта составляющая пропорциональна заряду е и не зависит от его скорости. Она направлена вдоль напряженности электрического поля Е.

Второе слагаемое в (15) дает силу, действующую на заряд со стороны магнитного поля. В отличие от электрической силы, она действует только на движущийся заряд и пропорциональна его ско­рости. Эта сила направлена не вдоль, а поперек вектора магнитной индукции В, т. е. перпендикулярно магнитным силовым линиям.

Формула (15) имеет универсальный характер, она справедлива во всех случаях независимо от того, какими источниками создаются электрическое и магнитное поля. Она сохраняет свой вид и тогда, когда действующие на заряженную частицу электрическое и маг­нитное поля неоднородны в пространстве и произвольным образом изменяются со временем.

3.3. Движение заряженных частиц в магнитном поле

П ри заданных полях 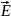и задача о движении заряженной частицы – это обычная задача клас­си­ческой механики о движении под действием известных сил. В однородных электри­чес­ком и магнитном полях движение заряженной частицы про­исходит достаточно просто и может быть изучено элементарными методами.

Д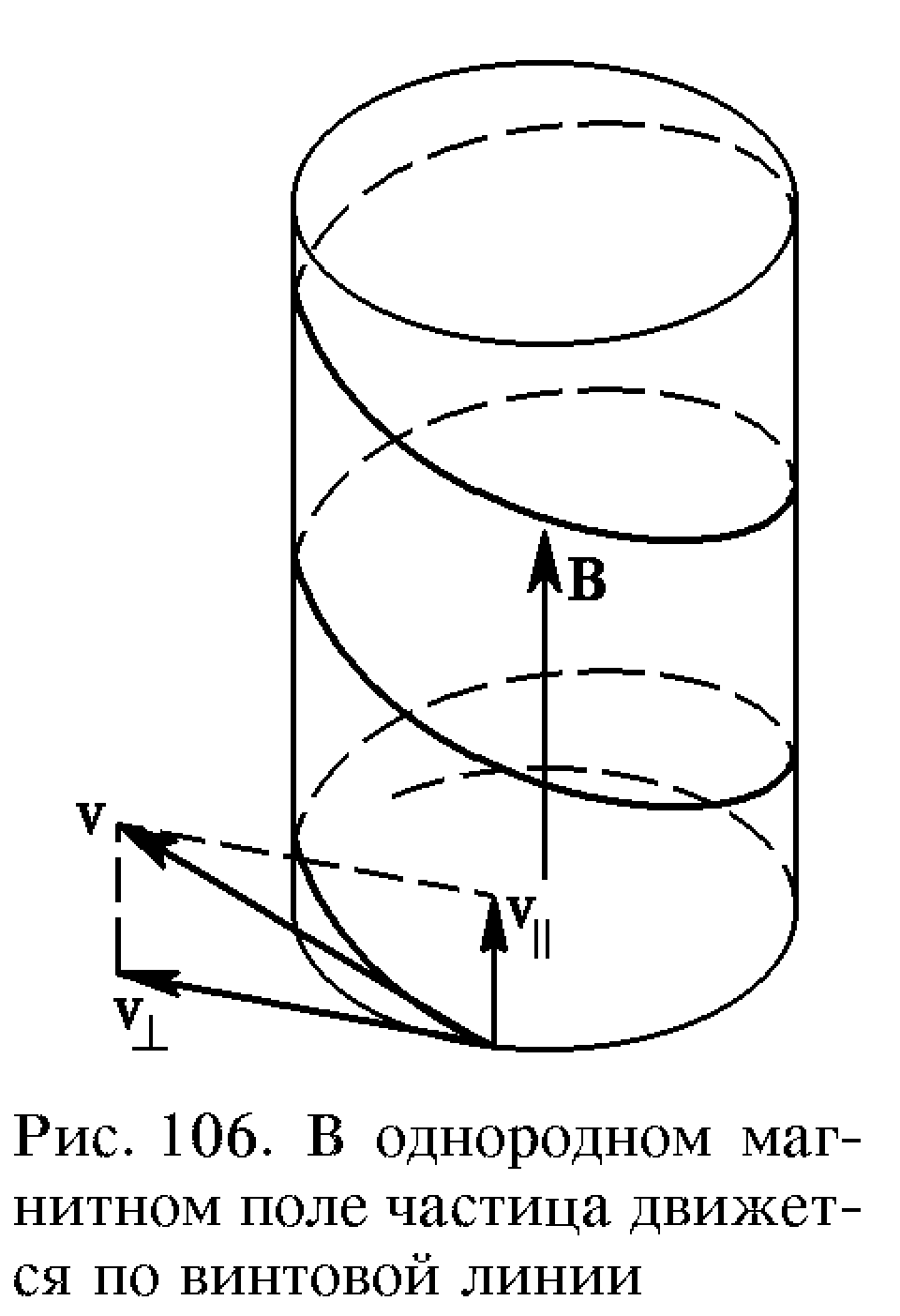 вижение заряженной частицы в однородном магнитном поле под действием силы Лоренца 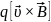происходит следующим образом. В плоскости, перпендикулярной индукции магнитного поля, частица равномерно обращается по окружности со скоростью υ (рис. 105). Ра­диус R этой окружности пропорционален перпендикулярной магнитному полю составляющей скорости части­цы υ_, а частота обращения частицы ω_с от скорости не зависит и равна произведению удельного заряда частицы на индукцию магнитного поля. Если при этом частица имеет еще и составляющую скорости υ_|| вдоль магнитного поля , то на такое вра­щение накладывается равномерное движе­ние вдоль поля, так что траектория резуль­тирующего движения представляет собой винтовую линию (рис. 106). Покажем это.

Составляющая скорости частицы вдоль магнитного поля υ_|| и не меняется при движе­нии. Cо­ста­вляющая скорости, перпендику­лярная магнитному полю, υ_ меняется только по напра­вле­нию, так как действующая сила перпендикулярна скорости, поэтому в проекции на плоско­сть, перпендикулярную магнитному полю, движение частицы проис­ходит по окружности неко­то­рого радиуса R с центростремительным ускорением 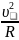, обусловленным силой Лоренца. Записывая выражение для этой силы в виде qυ_ В и приравнивая ее в соответствии со вто­рым законом Ньютона произведению массы на ускорение, имеем

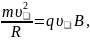
откуда

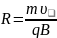(16)

Частота обращения частицы ω_с = 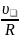, как видно из (16), равна:

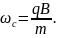(17)

Независимость частоты обращения частицы в магнитном поле от ее скорости и от радиуса круговой орбиты (а тем самым и от энергии) лежит в основе принципа действия циклотрона исторически первого и наиболее простого из циклических ускорите­лей заряженных частиц, широко применяемого и в наши дни в самых различных областях науки и техники. От названия этого прибора происходит термин «циклотронная частота» для частоты обращения заряженной частицы в магнитном поле, даваемой формулой (17). Отклонение заряженных частиц поперечным магнитным полем используется также в масс-спектрометрах — приборах для точных измерений масс атомов и молекул, в установках для электро­магнитного разделения изотопов. В телевизионных трубках с по­мощью магнитного поля производится строчная и кадровая развер­тка электронного луча по экрану.