Описание экспериментальной установки

Общий вид прибора FPM – 13 представлен на рис. 4 а, б. Основание 1 оснащено регулирующими винтами, обеспечивающими выравнивание прибора. В основании закреплена колонка 2. На колонке закреплена втулка 3 и кронштейн 4. На стержне 5 втулки находятся три подвески 6, на которых подвешены в подшипниках два маятника и стержень 7, возбуждающий колебания. Маятник состоит из стержня 8 и перемещаемого груза 9.

М

а) б)

Рис. 4 Экспериментальная установка FPM-13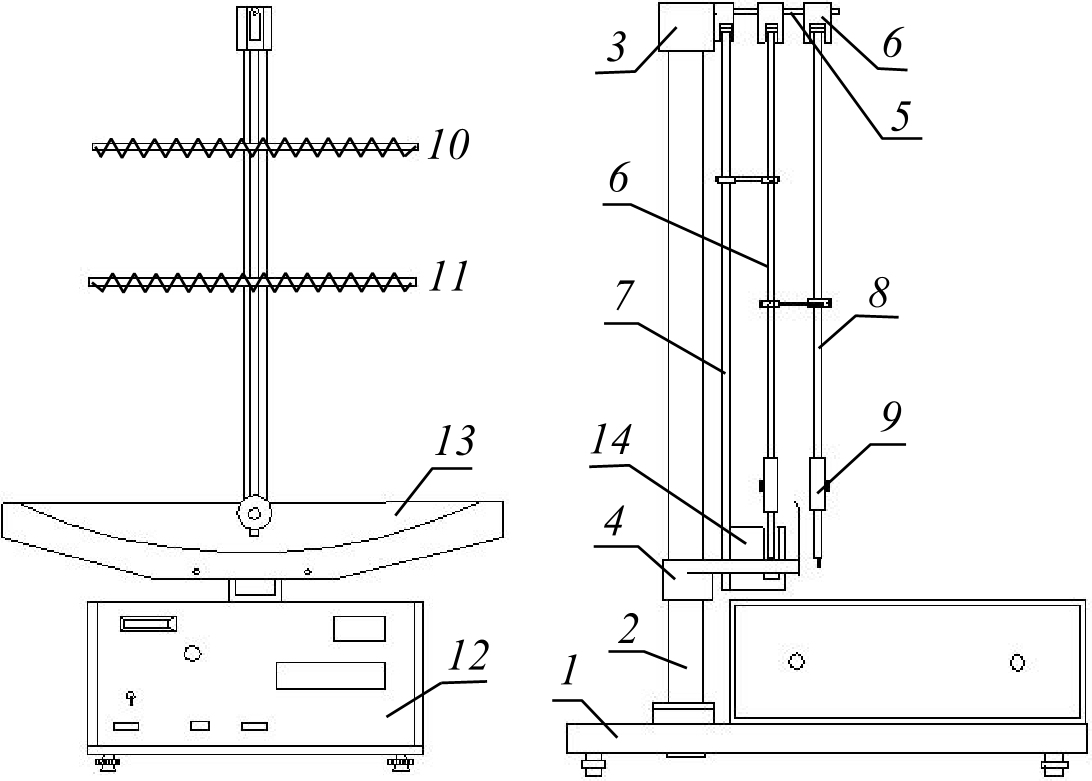

аятники сопряжены друг с другом при помощи двух пружин 10, закрепленных в – образной обойме 11, которую можно перемещать вдоль стержней маятников. Возбуждение колебаний осуществляется при помощи приводного диска, закрепленного на валу электродвигателя, который, двигая стержень 7, сопряженный при помощи двух пружин 10 со стержнем маятника, возбуждает его колебания. Электродвигатель находится в блоке управления и измерения 12. К нижнему кронштейну прикреплена угловая шкала 13, при помощи которой определяется амплитуда колебаний маятников. К нему прикреплен также фотоэлектрический датчик 14, световой поток от которого пересекает стержень одного из совершающих колебания сопряженных маятников.

Задания к лабораторной работе

1. Определить частоту синфазных и противофазных колебаний сопряженных маятников

Для определения частоты синфазных колебаний следует:

• установить обоймы, крепящие пружины, на верхней части стержней маятников, а грузы на нижней части стержней на одинаковом расстоянии от концов;

• отсоединить пружины от обоймы, соединяющей маятники со стержнем, возбуждающим колебания;

• нажать кнопку «Сеть»;

• отклонить маятники в одинаковую сторону на угол около 6^о и отпустить их;

• нажать переключатель «Сброс»;

• после подсчета прибором около 10 периодов колебаний нажать кнопку «Стоп»;

• записать время и количество колебаний, считав их с индикаторов.

Вычислить частоту синфазных колебаний по формуле:

,

где - количество периодов колебаний, - продолжительность измерений.

Измерение частоты противофазных колебаний производится аналогично, но маятники надо первоначально отклонить в противоположные стороны на угол около 6^о и отпустить.

2. Изучить явление биений

Для наблюдения биений необходимо:

• отсоединить пружины от обоймы, сопрягающей маятники со стержнем, возбуждающим колебания;

• установить произвольные параметры маятников;

• один из маятников отклонить на угол около 30^о и отпустить, наблюдать происходящие явления.

3. Изучить явление резонанса

Для наблюдения резонанса необходимо:

• наложить пружины на обойму, сопрягающую маятники со стержнем, возбуждающим колебания;

• включить питание электродвигателя;

• регулируя обороты электродвигателя, наблюдать амплитуду колебаний маятников;

• при резонансе маятники колеблются с амплитудой около 20^о.

Вопросы

1. Гармонические колебания.

2. Математический и физический маятники.

3. Вынужденные колебания.

4. Резонанс.

5. Биения.

Литература

1. Пономаренко В.И., Ильин Ю.М. Курс общей физики. Механика. – Киев: Изд-во «ВИПОЛ», 1997. – 212 с.

2. Сивухин Д.В. Общий курс физики. Механика. – М.: Наука, 1974.

Лабораторная работа №6

Определение модуля Юнга методом Лермантова

Оборудование: прибор Лермантова, микрометр, грузы, зрительная труба, масштабная линейка.

Теоретическая часть

Под действием приложенных сил все реальные тела деформируются, изменяя свою форму или объем. В случае твердого тела деформации можно разделить на упругие, практически исчезающие после прекращения действия на тело сил, и пластические (остаточные), которые сохраняются полностью или частично и после прекращения действия сил. Является деформация упругой или пластической, зависит не только от материала тела, но и от величины приложенных сил.

Идеально упругими называются такие деформации, величина которых однозначно определяется приложенными силами. Понятно, что идеально упругие деформации не существуют, это идеализация. Однако, эта идеализация часто очень близка к реальности.

Для тел, обладающих идеальной упругостью, в случае достаточно малых деформаций выполняется закон Гука: величина деформации пропорциональна силам, ее вызвавшим. Покажем это на примере стержня, подвергающемуся продольному растяжению (сжатию). Обозначим через длину недеформированного стержня, а через - величину деформации. Величина называется относительным удлинением. Поскольку стержень абсолютно упругий, то деформирующая сила является однозначной функцией удлинения, . Разложим в ряд Тейлора по степеням

, (1)

где , , - не зависящие от коэффициенты. Поскольку нулевой деформации соответствует нулевая сила, то . Если деформация достаточно мала, то , и в формуле (1) можно пренебречь членами высшего порядка малости, положив

.

Силы, обеспечивающие некоторое фиксированное относительное удлинение разных стержней из одного и того же материала, очевидно, не зависят от длин стержней и прямо пропорциональны площади сечения стержней. Следовательно, коэффициент , не зависит от длины стержня и прямо пропорционален его площади сечения

. (3)

Величина определяется лишь свойствами того материала, из которого сделан стержень и называется модулем упругости или модулем Юнга данного материала. Из (2), (3) находим

; . (4)

Кроме растяжения, наиболее важными в практике являются деформации кручения, изгиба и сдвига.

Рис. 1 Установка Лермантова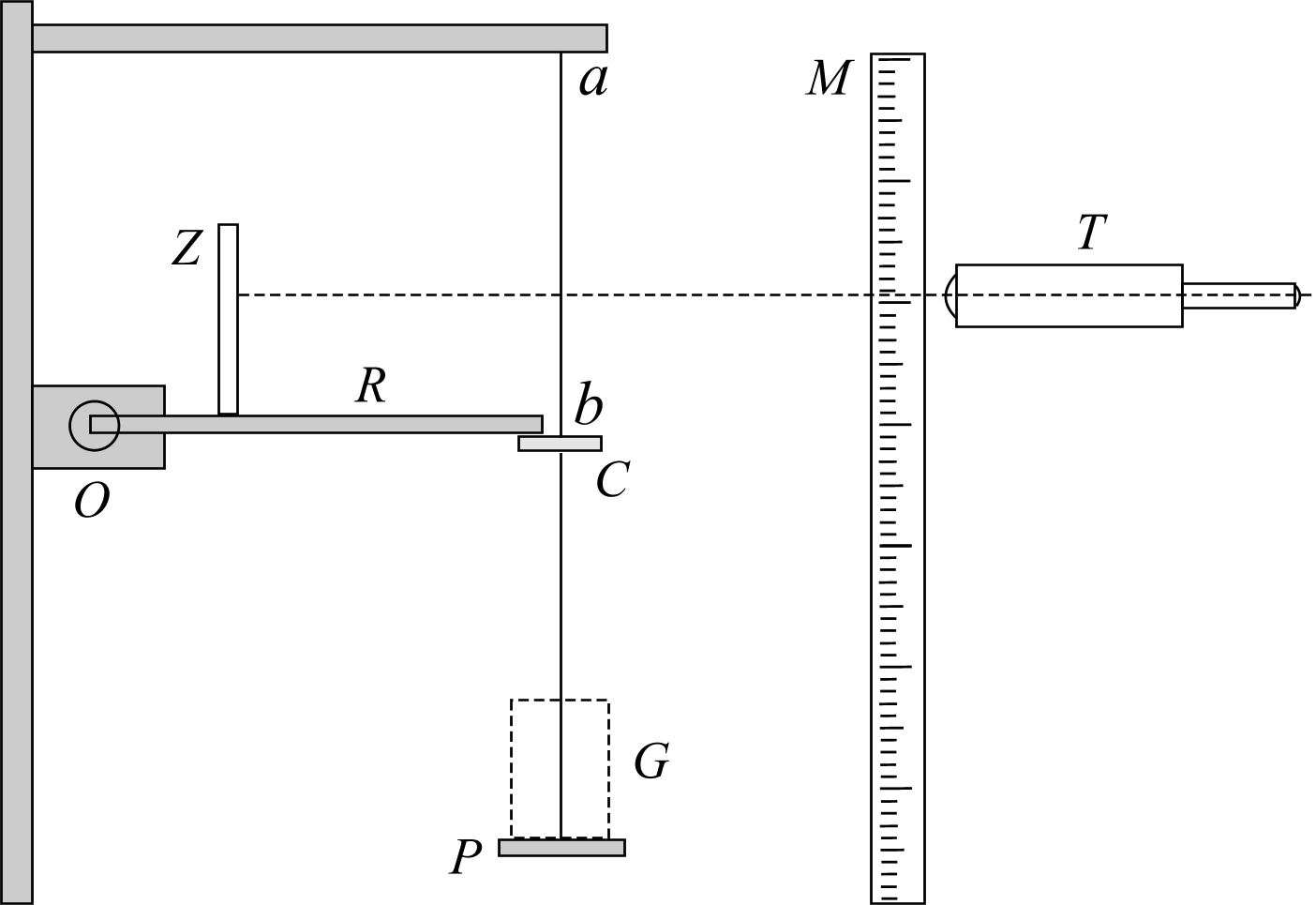

Целью настоящей работы является опытное определение модуля Юнга. Метод основан на том, что, растягивая с известной силой тонкий стержень (проволоку) и измеряя удлинение, можно из формулы (4) вычислить модуль Юнга

. (5)

Для точного измерения удлинения (оно обычно мало) применяется прибор, изображенный на рис. 1. На кронштейне подвешена испытуемая проволока. К ее нижнему концу прикреплена площадка , на которой можно размещать грузы с целью растяжения проволоки. На проволоке закреплен цилиндр , на который опирается конец рычага . Рычаг , вместе с установленным на нем зеркальцем может поворачиваться вокруг горизонтальной оси , закрепленной в кронштейне. При удлинении на отрезка проволоки зеркальце вместе с рычагом повернется на угол (рис. 2), удовлетворяющий соотношению

, (6)

Рис. 2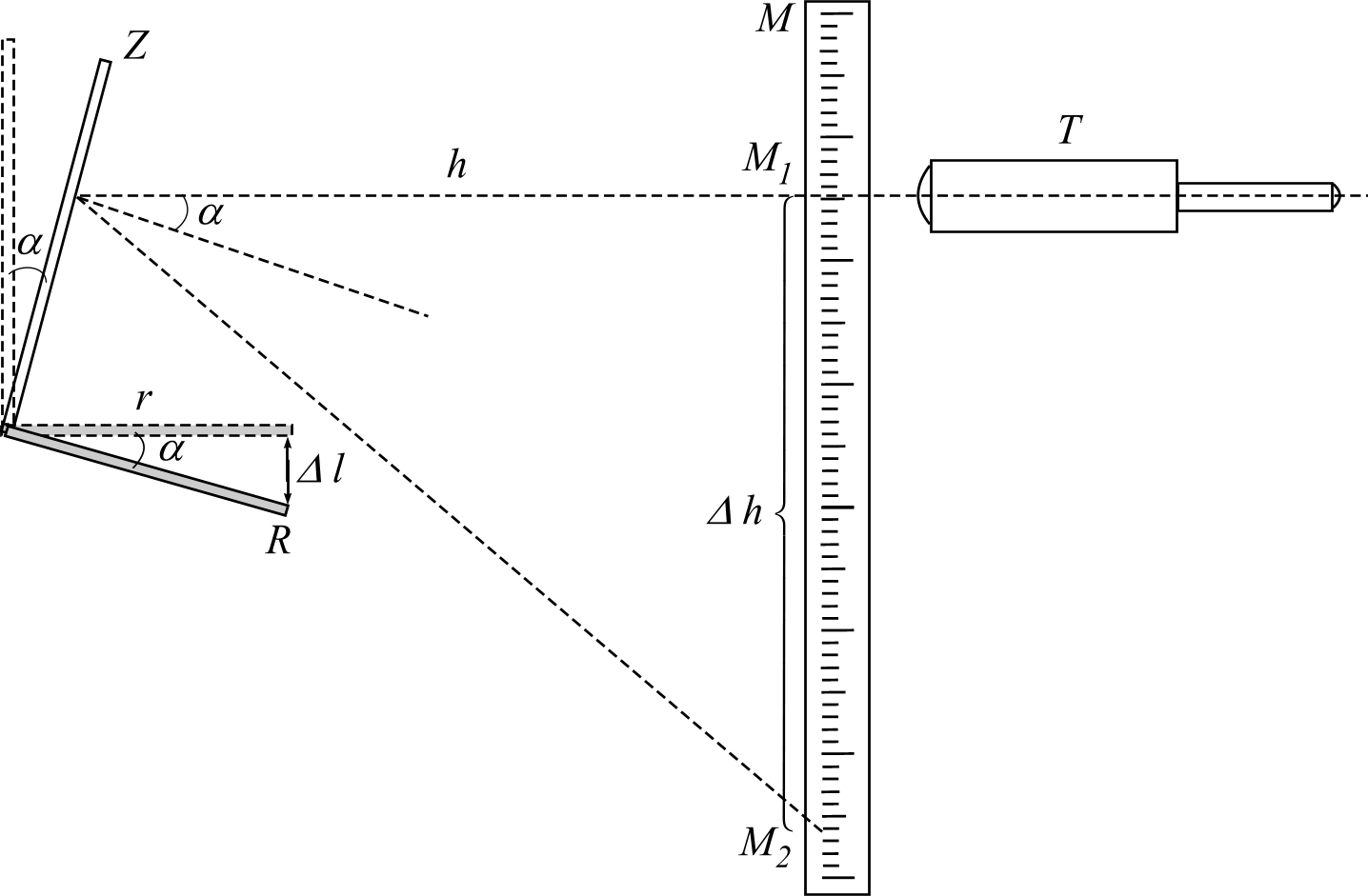

где - длина рычажка . Поворот зеркальца фиксируется с помощью подзорной трубы, через которую рассматривается отраженная в зеркальце масштабная линейка . Если до поворота зеркальца через перекрестье трубы была видна метка , то после поворота на угол будет видна метка . При этом

. (7)

Ввиду малости угла можно положить

, ,

при этом получим из (6), (7)

. (8)

Задания к лабораторной работе

1. Измерить диаметр проволоки микрометром в нескольких местах и вычислить ее площадь сечения .

2. Измерить длину проволоки от верхнего крепления до цилиндра, расстояние от зеркальца до шкалы и длину рычажка, на котором укреплено зеркальце.

3. Записать значения , , , .

4. При ненагруженной проволоке установить шкалу и трубу так, чтобы была видна в трубе шкала, отраженная в зеркальце, и зафиксировать ту метку шкалы, которая совпадает с перекрестьем трубы. Затем то же самое проделать при нагруженной проволоке и определить величину . Измерения проделать пять раз для разных грузов.

5. По результатам измерений вычислить модуль Юнга в единицах системы СИ ( ).

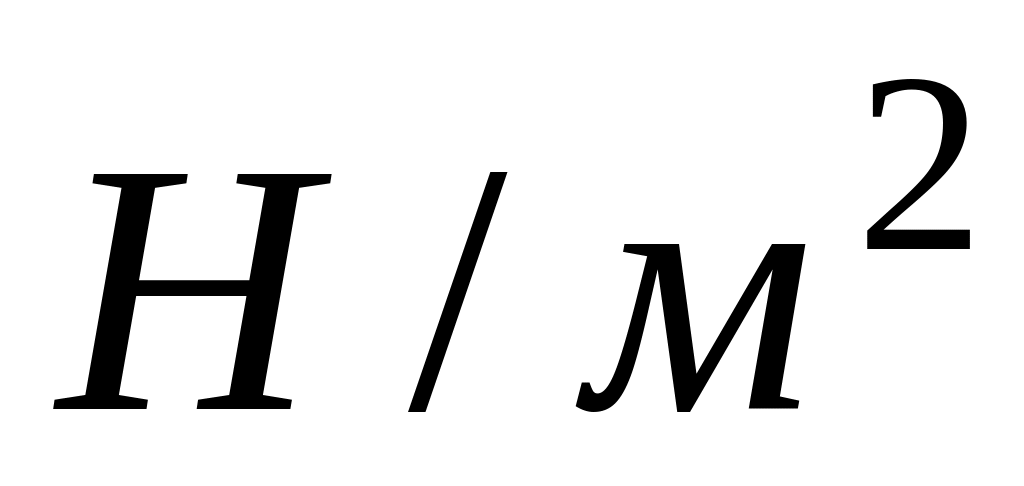6. Оценить абсолютную и относительную погрешность.

7. Результаты измерений и вычислений занести в табл. 1.

Таблица 1.

№	, Н	, м	, Н/м2	, Н/м2
1.
2.
3.
4.
5.

Выписать найденное значение модуля Юнга .

Вопросы

1. Упругие и пластические деформации.

2. Виды деформаций: сжатие, кручение, сдвиг, изгиб.

3. Закон Гука.

Литература

1. Пономаренко В.И., Ильин Ю.М. Курс общей физики. Механика. – Киев: Изд-во «ВИПОЛ», 1997. – 212 с.

2. Сивухин Д.В. Общий курс физики. Механика. – М.: Наука, 1974.

3. Стрелков С.П. Механика. М.: Наука, 1975.

4. Матвеев А.Н. Механика и теория относительности. М.: Высшая школа, 1976.

Лабораторные работы по курсу общей физики.

Механика. Часть III.

Составители:

Пономаренко Владимир Иванович, профессор кафедры экспериментальной физики,

Лагунов Игорь Михайлович, старший преподаватель кафедры экспериментальной физики.

Подписано к печати	Формат 60х84.16	Бумага тип. ОП
Объем п.л.	Тираж 200	Заказ

Таврический Национальный университет имени В.И.Вернадского

95007, Симферополь, ул. Ялтинская, 4

34