Определение погрешности

Проверка точности производится по формуле

, ⁽¹²⁾

где - импульс шаров до столкновения,  импульс шаров после столкновения.

Проверку точности измерения продолжительности столкновения шаров можно произвести путем измерения частоты схемы генератора. Для этой цели надо отвинтить и снять верхнюю плату прибора и изменить частоту сигнала в точке . Измеряемая частота должна иметь значение .

^{Вопросы}

1. ^{Импульс. Законы сохранения импульса и энергии.}

2. ^{Столкновения, законы сохранения при столкновениях.}

3. ^{Охарактеризуйте упругие столкновения.}

Литература

1. Пономаренко В.И., Ильин Ю.М. Курс общей физики. Механика. – Киев: Изд-во «ВИПОЛ», 1997. – 212 с.

2. Сивухин Д.В. Общий курс физики. Механика. – М.: Наука, 1974.

3. Стрелков С.П. Механика. М.: Наука, 1975.

4. Матвеев А.Н. Механика и теория относительности. М.: Высшая школа, 1976.

Лабораторная работа №3

Определение скорости пули с помощью баллистического маятника

Оборудование: баллистический маятник, воздушная винтовка, пули, измерительная шкала, весы с разновесами

Теоретическая часть

Одним из косвенных методов для определения скорости пули является метод, в котором используется неупругое соударение, в результате которого сталкивающиеся тела продолжают движение после соударения как единое целое. К таким методам относится и метод баллистического маятника.

Баллистическим маятником называется маятник, используемый для определения скорости быстро движущихся тел (пуль, снарядов и т.д.). Маятник представляет собой открытый с обоих концов цилиндр, наполненный пластилином и подвешенный на четырех длинных нитях. К цилиндру прикреплена указательная стрелка. Наблюдая перемещение стрелки вдоль шкалы, можно измерить величину отклонения маятника от положения равновесия. Выстрел производится из воздушной винтовки в центр основания цилиндра. Пуля попадает в пластилин и застревает в нем. Так как длина нитей подвеса значительно больше размеров цилиндра, значит при расчетах маятник можно считать математическим. Для расчета величины скорости пули по экспериментальным данным применяются законы сохранения импульса и энергии.

Рассмотрим сначала систему, состоящую из цилиндра и пули, которая летит горизонтально со скоростью , затем застревает в пластилине и далее начинает двигаться вместе с цилиндром (происходит полное неупругое соударение). Если время соударения пули с цилиндром много меньше периода колебаний маятника (условие применимости баллистического метода), то за время маятник практически не успевает выйти из положения равновесия. В этом положении на цилиндр действуют сила тяжести и силы натяжения нитей. На пулю непосредственно перед соударением действует только сила тяжести (сопротивлением воздуха пренебрегаем). Поскольку проекции всех этих сил на горизонтальное направление равны нулю, то справедлив закон сохранения импульса системы цилиндр-пуля для проекций на это направление.

Пусть масса пули, - масса цилиндра с пластилином. Непосредственно перед соударением импульс цилиндра равен нулю, проекция импульса пули на горизонтальное направление равна . Сразу после соударения, когда пуля уже прекратила свое движение, цилиндр и пуля движутся вместе с некоторой скоростью и имеют проекцию импульса на горизонтальное направление . Согласно закону сохранения импульса

.

Отсюда находим скорость пули

.

Р

Рис. 1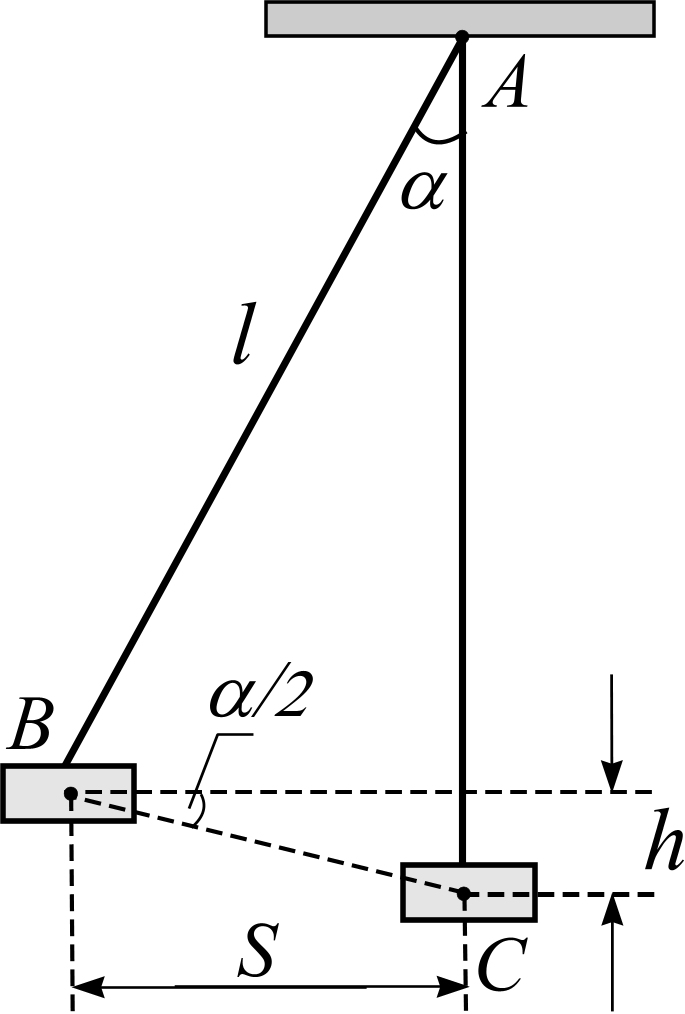

ассмотрим теперь систему, состоящую из цилиндра, вместе с застрявшей в нем пулей, и Земли (рис. 1). Для этой системы внешними силами являются силы натяжения нитей, а внутренней силой – сила тяжести. Силой трения в подвесе и сопротивлением воздуха при движении маятника можно пренебречь. Внешние силы работы над телами системы не совершают (точка подвеса неподвижна, нет движения цилиндра по дуге, равнодействующая сил натяжения нитей направлена по радиусу к центру этой дуги, т.е. перпендикулярно движению цилиндра). Внутренняя сила – сила тяжести – является потенциальной. Поэтому при дальнейшем движении маятника полная механическая энергия системы цилиндр-Земля будет оставаться постоянной. Потенциальная энергия здесь обусловлена силой тяжести и будет зависеть от взаимного расположения цилиндра и Земли.

Землю, как известно, можно с большой степенью точности принять за инерциальную систему отсчета. В этой системе отсчета положение Земли неизменно, а скорость ее равна нулю. Момент времени сразу после застревания пули примем за начальный. В этот момент маятник практически находится еще в положении равновесия, скорость цилиндра и его кинетическая энергия . Будем также считать, что в этот момент потенциальная энергия системы равна нулю. Таким образом, начальная энергия системы

.

Пусть конечным моментом времени является момент, когда отклонение маятника наибольшее. В этот момент скорость цилиндра и, следовательно, его кинетическая энергия равны нулю. Потенциальная энергия системы в этот момент определяется высотой на которую поднялся центр масс цилиндра относительно положения, при котором потенциальная энергия была принята за нуль. Таким образом, конечная энергия системы

.

Согласно закону сохранения энергии , т.е.

.

Найдем скорость пули

.

Величину можно найти, измерив наибольшее отклонение маятника от положения равновесия. Как видно из рисунка,

,

где - расстояние от центра масс цилиндра до точки подвеса, - угол отклонения маятника от положения равновесия.

Так как скорость маятника с пулей в крайнем положении равна нулю, отсюда . Из чертежа видно, . Так как угол мал, примем .

Угол находим из треугольника : .

Решая совместно уравнения, получим:

.

Надо иметь ввиду, что эта формула справедлива, если время движения системы пуля-маятник мало по сравнению с периодом его колебаний.

Задания к лабораторной работе

1. Установить баллистический маятник и шкалу таким образом, чтобы нити подвеса не перекрещивались, чтобы стрелка была расположена против нулевого деления шкалы.

Масса маятника , масса пули и длина маятника записаны на лабораторной установке.

2. Определить смещение маятника после выстрела

Для определения смещения маятника один из студентов, выполняющих работу, внимательно следит за смещением стрелки баллистического маятника по измерительной шкале, а другой производит выстрел из воздушной винтовки в центр основания цилиндра баллистического маятника. Наблюдатель записывает показание наибольшего смещения стрелки, стараясь оценить смещение с точностью до половины деления шкалы. Опыт повторяют несколько раз, для дальнейшей статистической обработки.

3. Обработать результаты измерений

Результат определения смещения маятника обрабатывают по теории случайных ошибок для малого числа повторений опыта. Случайная ошибка среднего арифметического не может быть меньше инструментальной ошибки, которая в данном случае достигает .

Оценив погрешности , , , , найти абсолютную ошибку результата вычисления. При нахождении погрешности косвенного измерения скорости, в числителе рабочей формуле пренебрегают массой , по сравнению с массой . Получим формулу для нахождения погрешности измерений скорости, для этого расчетную формулу для скорости

сначала прологарифмируем, а затем продифференцируем, получим

.

Заменяя дифференциалы ошибками, а сумму – средними квадратичными, получим

,

если какое-нибудь слагаемое под корнем значительно меньше других, то его можно отбросить, упростив вычисления.

Вопросы

1. Законы сохранения импульса и энергии.

2. Назовите критерии, по которым маятник может считаться баллистическим.

3. Охарактеризуйте абсолютно неупругое соударение.