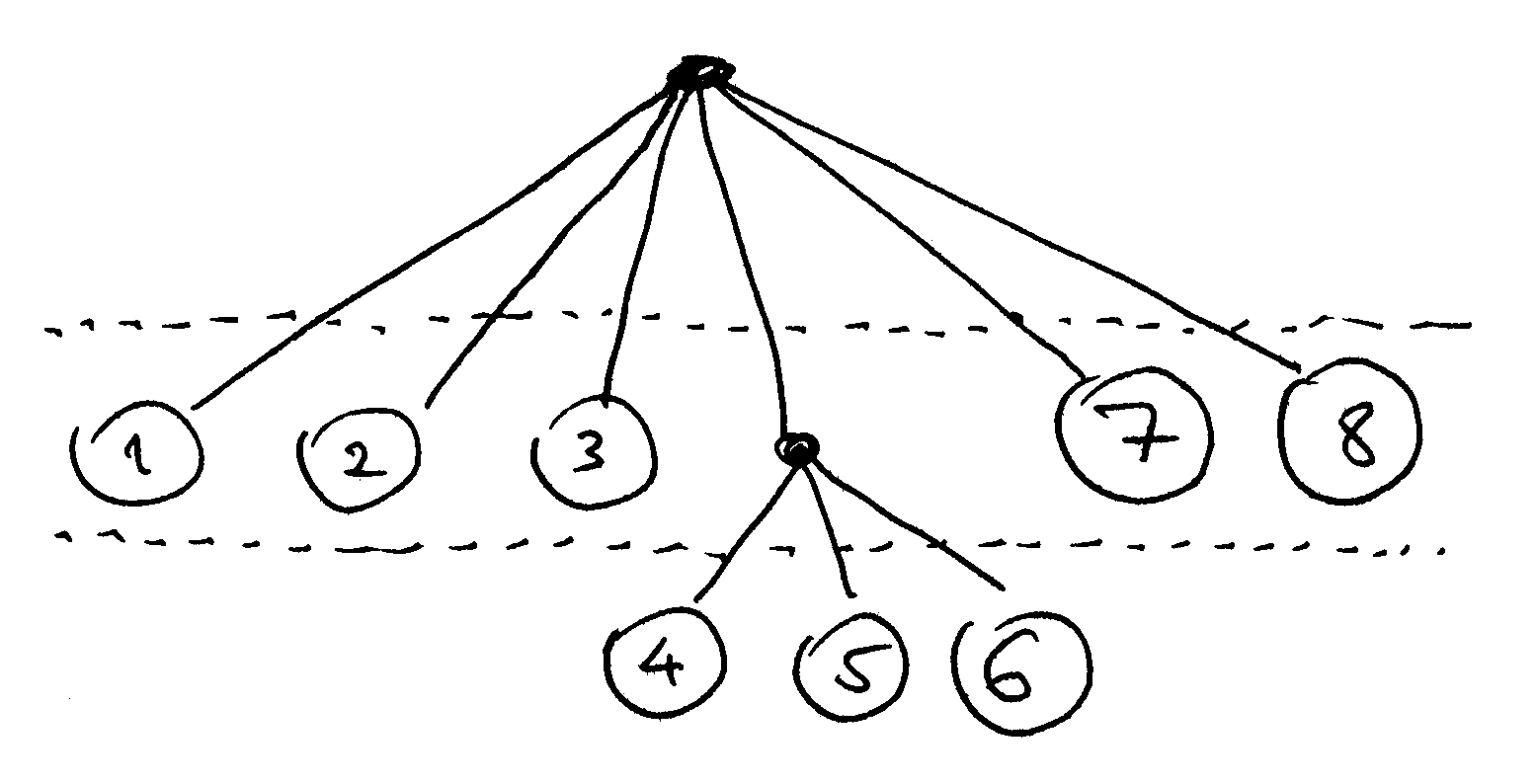
6.2.4 Представление древовидных структур
Списки, элементами которых в свою очередь являются списки, можно интерпретировать как деревья. Элементы списка - это во-первых листья. Подсписки образуют ветви со своими листьями или следующими ветвями.
Рекурсия - естественный инструмент для работы с древовидными структурами, так как мы можем сводить операции на деревьях к операциям на их ветвях, которые в дальнейшем приводят к операциям на ветвях ветвей, и так далее, пока не достигнем уровня листьев дерева.
Определим , например, функцию count-leaves, возвращающую число листьев дерева.
Для пустого дерева оно равно 0, для листа - 1.
Наконец, если дерево представляет собой список ветвей, то число листьев в нём равно сумме числа листьев в первой ветви и числа листьев в остальных ветвях.
Получаем, не забывая заранее определить предикат atom?, такую функцию:
> (define (count-leaves tree)
(cond ((null? tree) 0)
((atom? tree) 1)
(else
(+ (count-leaves (car tree))
(count-leaves (cdr tree))))))
> (count-leaves '(1 2 3 (4 5 6) 7 8))
8
Заметим, что эта процедура учитывает все уровни дерева, а не только первый.
Ещё одна проверка функции.
> (count-leaves '(1 (2 3) (4 5 (6)) 7 8))
8
Зная о великой силе обобщения, мы немедленно записываем аналог функции свёртки для деревьев.
>(define (tree-fold op expr st tree)
(cond ((null? tree) expr)
((atom? tree) st)
(else (op (tree-fold op expr st (car tree))
(tree-fold op expr st (cdr tree))))))
> (tree-fold + 0 1 '(1 (2 3) a b (4 5(6)) 7 8))
10
Действительно, в указанном дереве содержится 10 листьев!