5.3 Элементы систем упрощения алгебраических выражений

Упростить алгебраическое выражение - это значит привести его к виду с минимальным числом операций и скобок

Риторический вопрос, что проще?

x+x или 2*x

3*a + 3*b или 3*(a+b)

(y+4)/2 или y/2 + 2

Для разных точек зрения будут разные ответы:

• человеческое восприятие

• экономичность хранения в памяти

• скорость дальнейшего преобразования

В развитых САВ существует набор так называемых флагов, устанавливая которые можно выбирать любую форму «простоты».

Наши правила упрощения будут таковы.

1. будем выбрасывать 0, если он входит как слагаемое

2. будем выбрасывать 1, если он сомножитель

3. будем выбрасывать скобки, которые не меняют приоритета действий

4. будем заменять на 0 всё выражение, где сомножителем встретится 0

Сначала опишем функцию (Remove x lst) , которая удаляет из списка lst заданный элемент x. На выходе получается снова список, но который не содержит указанного элемента. ВАЖНОЕ ОГРАНИЧЕНИЕ. Действие этой функции не распространяется на подсписки и касается только верхнего уровня.

>(define (Remove x lst)

(cond ((null? lst) '())

((eq? x (car lst)) (Remove x (cdr lst)))

(else (cons (car lst) (Remove x (cdr lst)))))))

Примеры её работы.

> (Remove 2 '(2 1 2 45 2))

(1 45)

> (Remove 2 '(2 a (2 45) 2))

(a (2 45))

> (Remove 2 '(2 2))

()

5.3.1 Теперь, возьмём на упрощение первый пример. Он был таким:

> (diff '(+ 123 x) 'x)

(+ 0 1)

Мы должны получить 1, причём без скобок. Видимо необходимы две функции. Первая из них должна выбрасывать из суммы все нули, (наше правило №1) т.е. делать следующего типа преобразование входного списка (+ 0 X 0) ==> (+ X)

Задача может быть сведена к выбрасыванию нулей из входного списка. Тогда справедливо считая, что входной список начинается со знака «+», запишем эту функцию так:

>(define (No-Plus-0 Exprs)

(Remove 0 Exprs))

Пример

> (No-Plus-0 '(+ 0 1))

(+ 1)

Теперь нужна функция, которая выбрасывает бессмысленный знак плюс, а заодно и превращает список из одного элемента в просто элемент, т.е. делает такое преобразование: (+ X) ==> X

>(define (No-Plus-Single Exprs)

(cadr Exprs) )

Пример

> (No-Plus-Single '(+ 1))

1

Или объединяя обе функции (выбрасываем из слагаемых 0 и убираем лишние скобки)

>(No-Plus-Single (No-Plus-0 '(+ 0 1)))

1

Чтобы такое упрощения сработало верно, необходимо быть уверенным, что выражение начинается со знака «+». Значит, необходим предикат:

>(define (Plus? Exprs)

(and (list? Exprs)

(eq? '+ (car Exprs))) )

И, наконец, сделаем функцию упрощения «нуля-с-плюсом-вначале»

>(define (SimplPlus-0 Exprs)

(if (Plus? Exprs) (No-Plus-Single (No-Plus-0 Exprs)) Exprs)))

Её проверка

> (SimplPlus-0 '(+ 0 1))

1

> (SimplPlus-0 '(- 0 1))

(- 0 1)

>

Разумеется, не нужно упрощать выражение, которое к нам не относится, поэтому оно возвращается неизменённым! Первое упрощение готово.

5.3.2 Второй пример на упрощение. Ранее у нас получилось

> (diff '(* x x) 'x)

(+ (* 1 x) (* 1 x))

Нам нужно, чтобы стало: (x²)’ = 2*x.

Для этого упрощения придётся написать две функции. Первая должна реализовывать наше правило №2, а именно, выбрасывать единицы из всех списков второго уровня (в наших выражениях – это сомножители).

>(define (No-Times-1 Exprs)

(cond ((null? Exprs) '())

((not (list? (car Exprs))) (cons (car Exprs)

(No-Times-1 (cdr Exprs))))

(#t (cons (Remove 1 (car Exprs))

(No-Times-1 (cdr Exprs))))))

Проверка

> (No-Times-1 '(+ (* 1 x) (* 1 x)))

(+ (* x) (* x))

Поскольку мы не проверяем правильность входного выражения, можно получить и не правильное упрощение:

> (No-Times-1 '(+ 1 y (* 1 y 2) (- 1 y)))

(+ 1 y (* y 2) (- y))

Вывод. Функции внутреннего упрощения создаются в облегчённом виде и только для пояснения работы системы упрощения.

Теперь нужно сделать вторую функцию, убирающую ненужные скобки (наше правило №3). Другими словами, она должна делать такое преобразование: ( (* X) ) ==> ( X )

>(define (No-Times-Single Exprs)

(cond ((null? Exprs) '())

((not (list? (car Exprs))) (cons (car Exprs)

(No-Times-Single (cdr Exprs))))

(#t (cons (cadar Exprs) (No-Times-Single (cdr Exprs))))))

Надо обратить внимание на выражение (cadar Exprs). Именно таким способом получается «выковырять» переменную x в «чистом виде» из скобочного выражения ((* x))

Проверка

> (No-Times-Single '(+ (* x) (* x)))

(+ x x)

Реализация алгоритма приведения подобных членов слишком сложна, чтобы быть реализованной простой функцией, поэтому остановимся на этом результате.

Ответ не так хорош, как хотелось бы (хотелось бы = 2*x !!!), но по крайней мере, уже обозрим.

5.3.3 Итак, рассмотрим последний пример упрощения

> (diff '(+ (* x 2)(* x x)) 'x)

(+ (+ (* 1 2) (* 0 x)) (+ (* 1 x) (* 1 x)))

Вместо этих запутанных скобок желательно получить: 2 + 2*x

Во-первых, нам понадобится функция, которая ищет списки второго уровня (для нас - это суть произведения), в которых есть 0, и если таковые есть, то возвращает вместо каждого - нуль. (Наше правило №4).

Итак, преобразование ((* … 0 …)) ==> ( 0 )

>(define (No-Times-0 Exprs)

(cond ((null? Exprs) '())

((not (list? (car Exprs))) (cons (car Exprs)

(No-Times-0 (cdr Exprs))))

(#t (cons ((lambda (Lst)(if (member 0 Lst) 0 Lst)) (car Exprs))

(No-Times-0 (cdr Exprs))))))

Применяемая здесь лямбда-функция возвращает 0, если в списке, получаемом с помощью (car Exprs), найдётся хотя бы один 0. Иначе ничего не происходит.

Проверим.

> (No-Times-0 '(+ (* 0 x) (* 1 x)))

(+ 0 (* 1 x))

Теперь последние две функции.

Первая служит такому преобразованию: (+ A B C) ==> (A B C)

Ее смысл: Если в S-выражении первым стоит знак плюс – то этот знак выбрасывается.

>(define (No-Sum-List Exprs)

(if (Plus? Exprs) (cdr Exprs)

(list Exprs)) )

Вторая – если есть сумма сумм, то все суммы в этой большой сумме объединяются в одну-единую сумму, т.е., она делает следующее: (+ (+ A B) C) ==> (+ A B C)

>(define (Consolidate-Plus Exprs)

(if

(Plus? Exprs)

(apply append (map No-Sum-List Exprs))

Exprs) )

Здесь следует пояснить, что написано в основной рабочей строчке последней функции.

Во-первых, MAP с функцией No-Sum-List образует новый список, убирая из входного выражения лишнее плюсы:

>(map No-Sum-List '(+ (+ (* 1 2) (* 0 x)) (+ (* 1 x) (* 1 x))))

((+) ((* 1 2) (* 0 x)) ((* 1 x) (* 1 x)))

Во-вторых, надо собрать списки под одно крыло, т.е. сделать единый список, что и делает функция append (но только для двух верхних списков !).

>(append '(+) '((* 1 2) (* 0 x)) )

(+ (* 1 2) (* 0 x))

А чтобы заставить её работать «в цикле» для множества списков, применена функция apply. (Мы подробнее рассмотрим ее позже). Cмысл действие которой такой же что и eval – заставить выполнятся функцию append, но на заданном списке.

Итак, попробуем последовательно применить эти функции.

> (Consolidate-Plus '(+ (+ (* 1 2) (* 0 x)) (+ (* 1 x) (* 1 x))))

(+ (* 1 2) (* 0 x) (* 1 x) (* 1 x))

> (No-Times-0 '(+ (* 1 2) (* 0 x) (* 1 x) (* 1 x)))

(+ (* 1 2) 0 (* 1 x) (* 1 x))

> (No-Times-1 '(+ (* 1 2) 0 (* 1 x) (* 1 x)))

(+ (* 2) 0 (* x) (* x))

> (No-Times-Single '(+ (* 2) 0 (* x) (* x)))

(+ 2 0 x x)

> (No-0 '(+ 2 0 x x))

(+ 2 x x)

Мы получили упрощённое выражение: 2 + x + x. И поскольку у нас нет функции приведения подобных членов, то это и есть наш долгожданный итог.

Надо обратить внимание, что все функции упрощения были написаны для конкретных примеров, поэтому не имели ни должных проверок входных данных, ни необходимого обобщения на случай списков любой вложенности. Заметим также, что под упрощением мы в основном подразумевали реализацию наших четырёх правил.

Было заметно, что работа всех функции напрямую зависит от формы написания алгебраических выражений, а это значит, чтобы совершать упрощения и с другими объектами (полиномами, интегралами и пр.) её надо сделать более обобщающей. Тогда способ представления алгебраических выражений станет не таким простым, что, естественно, повлечёт за собой и гораздо более сложные функции упрощения, что можно предположить ненароком выльется в отдельный курс, но это не является нашей целью.

Заканчивая экскурс в системы аналитических вычислений, и для удовлетворения любопытства, как работают САВ, приведем пример работы с нашими примерами свободно распространяемой системы, имеющей название JACAL.

Она интересна прежде всего тем, что написана именно на изучаемом нами диалекте LISP’а, т.е. на DrRacket.

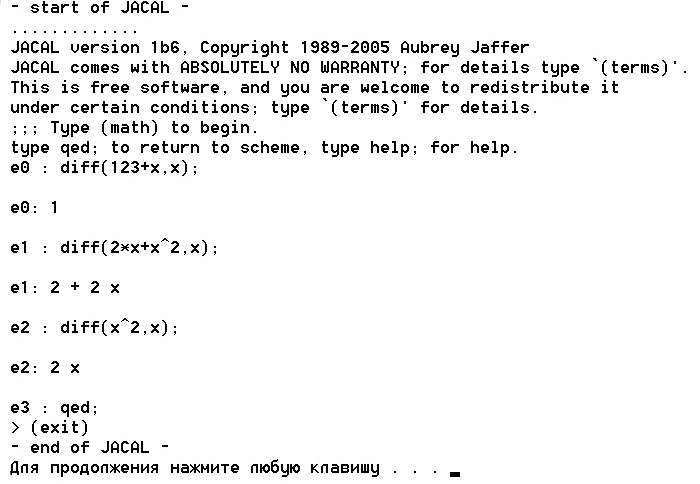
Конечно, такие результаты гораздо интереснее выглядят.

Но в любом случае, какими бы ни были результаты, даже и в «нечитаемом виде» - ими всё равно можно воспользоваться. Ну, разумеется если они правильные. А программы, как известно, должны работать вне зависимости от эстетического вида входных параметров.