4.3 Функционалы

4.3.1 Суммирование двух функций

Итак, мы рассмотрели использование функций в качестве аргументов.

Но можно значительно повысить нашу способность к абстрагированию, создавая функции, значениями которых также являются функции.

Функции, значениями которых также являются функции, называются функционалами

Пусть нам приходится неоднократно вычислять значение суммы двух известных функций, например sin(x)+cos(x). Конечно, мы можем определить эту сумму так:

> (define (sin+cos x) (+ (sin x) (cos x)))

Заметьте, какое интересное и содержательное название функции можно сделать в DrRacket !!

Теперь вызов с конкретным аргументом:

> (sin+cos 0.5)

1.3570081004945758

Однако, такое простое определение как-то не интересно.

Напишем функцию f+, вычисляющую значение суммы двух функций, но заранее не определенных, а задаваемых при вызове, например: f(x)+g(x).

>(define (f+ f g x) (+ (f x) (g x)))

Теперь, помимо аргумента, надо задать эти функции при вызове, чтобы получить, к примеру, такой результат:

> (f+ sin cos 0.7)

1.4090598745221796

Тем самым был определен функционал для вычисления значения суммы двух функций от заданного аргумента. Но как выразить саму идею суммирования функций, которая совершенно не зависит от обозначения аргумента? Надо спрятать аргумент в определение тела функции. Вспомним о лямбда-функции и перепишем определение f+ так:

> (define (f+ f g)

(lambda (x) (+ (f x) (g x))))

Аргумент исчез. Вернее он оказался внутри абстракции f+, которая возвращает функцию, вычисляющую значение суммы двух функций. Внешне всё выглядит теперь как именно сумма двух функций и, только при её вызове нам необходимо будет конкретизировать аргумент этих функций, подобно следующему примеру.

> ((f+ sin cos) 1.45)

1.113215760404955

4.3.2 Композиция функций

Другая полезная абстракция - композиция функций, т.е. многократный вызов функций от функций от функций …… и т.д.

Сначала определим композицию только двух функций f(x) и g(x).

> (define (comp f g)

(lambda (x) (f (g x))))

Для композиции sin(cos(x)) вызов будет таков:

> ((comp sin cos) 1.2)

0.35447986700952583

С помощью абстракции comp мы можем выразить идею двукратного применения одной и той же функции, т.е. f(f(x)):

> (define (twice f) (comp f f))

> ((twice sin) 0.9)

0.7056406678713629

Теперь совсем замечательно, с помощью этой функции можно создать функцию настоящей композиции, т.е. n-кратного применения одной и той же функции!

> (define (iter f n)

(if (= n 1) f

(comp f (iter f (- n 1)))))

> ((iter sin 2) 0.9)

0.7056406678713629

Перейдем к построению программ на языке ЛИСП, опираясь на известные математические функции.

4.4 Извлечение квадратного корня

4.4.1 Первая функциональная программа на lisp’е

Пусть перед нами стоит задача, написать функцию, вычисляющую квадратный корень заданного числа. Мы можем начать со спецификации искомой функции. Назовем ее squ

Общее замечание.

В реализации DrRacket эта функция встроена и называется sqrt.

И вообще, на будущее договоримся, чтобы избежать путаницы, будем давать нашим функциям свои (быть может странные) названия. Во-первых, чтобы не заменять встроенные функции - это дурной стиль. Есть ещё одна цель: всегда можно сравнить результаты.

Итак, есть уравнение

, где x>=0

Тогда x² = a, т.е., нам нужно найти такое x, квадрат которого в точности равен искомому корню.

Надо иметь в виду, что точное значения действительного числа, как правило, найти не удаётся. Это связано с представлением действительных чисел на компьютере. Поэтому будем осторожны и пока ограничимся «почти равенством», говоря, что значение x «достаточно близко» к квадратному корню из a, не уточняя пока, как это понимать.

Но как вообще вычисляют квадратные корни?

Воспользуемся методом Герона.

4.4.2 В качестве приближенного значения для квадратного корня из a возьмём произвольное число x.

Можно придумать такое тождество: 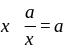, но важно заметить, что одно из двух значений или x или заведомо меньше искомого корня, а другое – больше его, а их среднее арифметическое будет ближе к корню.

Тогда, пожалуй, можно определить «улучшающую функцию» называя её, например, improve.

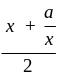( define (improve x a)

(/ (+ x (/ a x)) 2 ))

Как видно, она реализует такое выражение

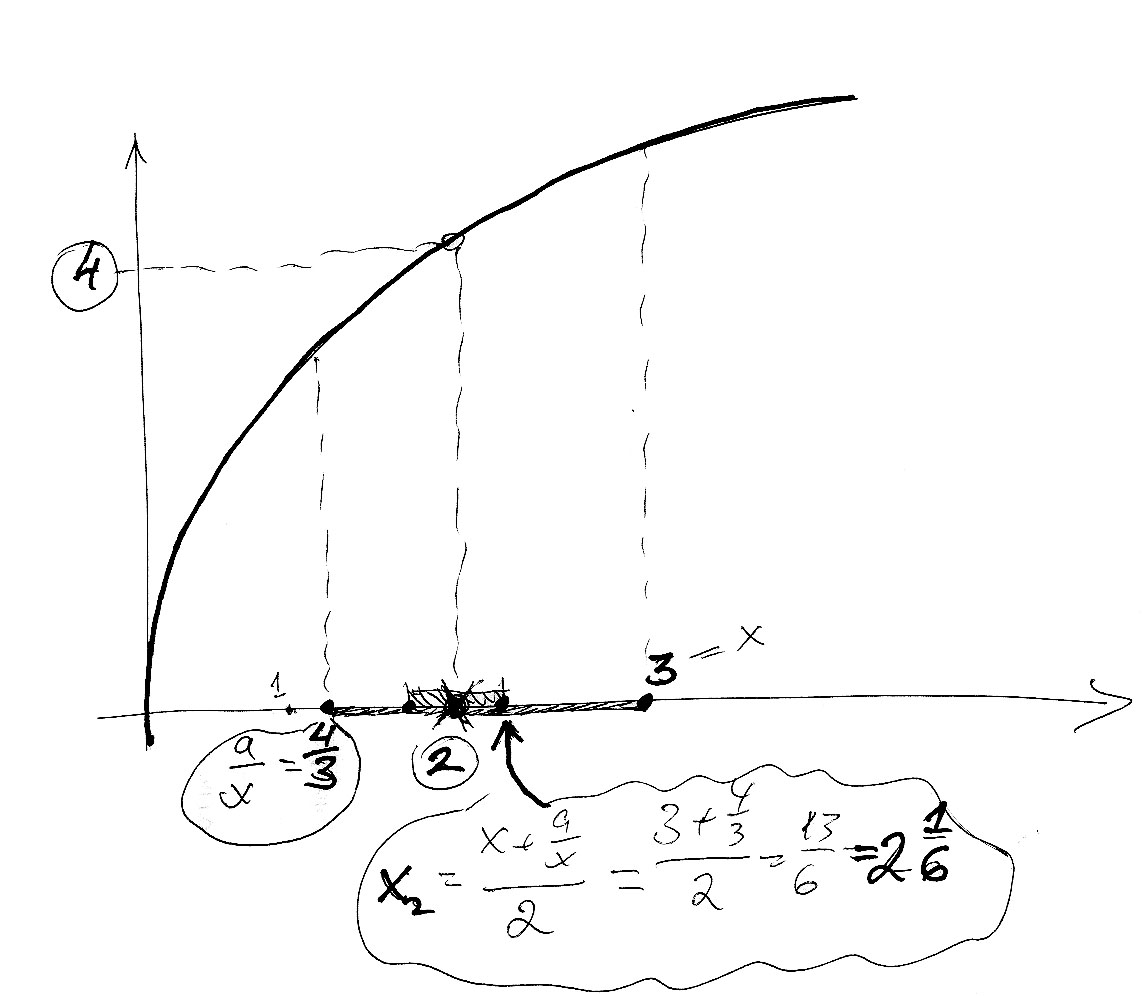
Последовательно применяя эту функцию для

вычисления следующего значения x мы будем приближаться к фактическому квадратному корню, пока не получим приемлемое (англ - acceptable) значение. (См. рисунок).

Таким образом, мы можем описать итерационный процесс приближения к истинному значению квадратного корня squ-iter так.

> (define (squ-iter x a)

(if (acceptable? x a) x

(squ-iter (improve x a) a)))

Итерация будет заключаться в том, чтобы на каждом шаге получать следующее значение х и затем проверять новое значение на приемлемость. А определить, что подразумеваеся под «приемлемым приближением», т.е. под предикатом acceptable?.

Первое предложение.

Приемлемым считаем такое значение x, когда квадрат найденного корня не будет отличаться от подкоренного выражения меньше чем на заданный допуск, т.е. удовлетворение выражению

> (define (acceptable? x a)

(< (abs (-(sqr x) a)) 0.01))

Наконец, требуется выбор начального приближения. Можно для начала предположить, что квадратный корень любого числа равен 1. (По крайней мере это не нуль!)

Теперь собирая все вместе, получаем нашу первую законченную (работающую!) программу на LISP.

> (define (squ1 a)

(squ-iter 1.0 a))

> (define (squ-iter x a)

(if (acceptable? x a) x (squ-iter (improve x a) a)))

> (define (improve x a)

(/ (+ x (/ a x)) 2 ))

> (define (acceptable? x a)

(< (abs (-(sqr x) a)) 0.01))

Проверим работу нашей процедуры нахождения корня

> (squ1 2)

1.4166666666666665

Некая неприятность состоит в том, что теперь никому нельзя использовать функции с названиями improve или acceptable?, потому что в squ1 эти имена уже задействованы.

4.4.3 Чтобы ограничить «область видимости» вспомогательных функций, т.е. функций, которые нужны только для промежуточных расчётов, над ввести их в область локальных определений, что аналогично понятию вложенных процедур.

Перепишем нашу функцию в виде:

> (define (squ2 a)

(define (acceptable? x a)

(< (abs (-(sqr x) a)) 0.001))

(define (improve x a)

(/ (+ x (/ a x)) 2 ))

(define (squ-iter x a)

(if (acceptable? x a) x (squ-iter (improve x a) a)))

(squ-iter 1.0 a) )

> (squ2 2)

1.4142156862745097

Кстати, почему результат отличается от предыдущего? – Изменён допуск!

Теперь acceptable?, squ-iter и improve видимы только внутри области определения squ2.