4. Функции высшего порядка

4.1 Введение

Язык программирования - не просто средство заставить компьютер выполнить те или иные действия. Мощный язык программирования должен обеспечивать возможность создавать абстракции, чтобы затем работать непосредственно в терминах этих абстракций.

Например, если бы мы определяли функцию возведения в квадрат (а мы так и сделаем!)

> (define (sqr x) (* x x))

то в дальнейшем, когда нужно было бы записывать возведение в квадрат, то необходимое бинарное умножение можно было заменить на вызов функции sqr.

. В версии DrRacket, версия 5.2.1 [3m], функция sqr определена и, поэтому, определять её не нужно.

Наша замена умножению хороша уже потому, что мы уходим от рассуждений в терминах умножения, и переходим на более высокий уровень. Более того, отказываясь от функции возведения в квадрат, наш алгоритмический язык оказался бы многословным и, как следствие, запутанным.

Поэтому практически все языки программирования содержат механизмы абстрагирования, т.е. средства для определения новых функций или процедур.

Способность оперировать функциями, используя их в качестве параметров или возвращаемых значений других функций есть свойство функций высшего порядка.

4.1.1 Функциональная концепция суммирования

Р ассмотрим два примера

1. Напишем функцию, вычисляющую сумму целых чисел от m до n.

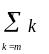
> (define (sum-int m n)

(if (> m n) 0

(+ m (sum-int (+ m 1) n))))

Проверим её работоспособность

> (sum-int 2 5)

1 4

2. Теперь функцию, вычисляющую сумму квадратов целых чисел от m до n

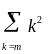
> (define (sum-sqr m n)

(if (> m n) 0

(+ (sqr m) (sum-sqr (+ m 1) n))))

> (sum-sqr 1 3)

14

Эти две функции чрезвычайно схожи. Различие только в общем члене суммы. Это наводит на мысль о множестве других подобных функций, а значит и о существовании полезной абстракции.

Давайте попробуем написать функцию, которая выражает концепцию суммирования с обобщённым членом суммы.

> (define (sum f m n)

(if (> m n) 0 (3Ш)

(+ (f m) (sum f (+ m 1) n))))

f- это общий член ряда суммирования, причём - это значение некоторой функции, которое вычисляется на каждом шаге итерации. Но оказывается, не всё так просто. Например, чтобы подсчитать сумму кубов чисел от 1 до 10, и справедливо записывая для f выражение в виде умножение из трёх переменных x, нельзя вызвать нашу новую функцию так:

(sum (* x x x) 1 10)

Получим ошибку:

> (sum (* x x x) 1 10)

reference to undefined identifier: x

Ошибка возникает из-за того, что LISP начинает выполнять задаваемое выражение (* x x x), но мы ещё не определили для x его начальное значение! Надо её не выполнять, а передать как функцию для выполнения. Возникает вопрос, а как же передавать в функцию не S-выражение, а именно функцию, вычисляющую требуемое выражение? (Вот где всплывает необходимость в функционале)

Вспомним о лямбда-выражениях, перепишем наш запрос, определяя куб как лямбда-функцию, и сразу же получим ответ:

> (sum (lambda (x) (* x x x)) 1 10)

3025

Вместо f была действительно подставлена функция, с которой произошли все рекурсивные вызовы, что и дало результат.

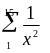
А теперь посчитаем и сумму и обратим внимание на замечательную форму ответа

> (sum (lambda (x) (/ (sqr x))) 1 15)

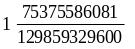
П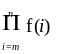 роцесс абстрагирования можно продолжить далее.

Например, совершенно аналогично можно определить функцию произведений

Назовём её prod, и будем требовать от неё вычисление произведения функций в заданном числовом интервале, а значит напишем:

> (define (prod f m n)

(if (> m n) 1

(* (f m) (prod f (+ m 1) n))))

А если теперь сравнить это произведение и ранее полученную сумму (см. 3Ш ), то напрашивается вывод, о попытке получения ещё более общего шаблона для «накопления»