3.5.1 Lambda – функция в Racket

Эта функция реализуется следующим стандартным выражением

(lambda (x₁…x_n) expr)

она возвращает функцию, вычисляющую значение выражения expr при подстановке фактических параметров вместо x₁…x_n.

Функция, определенная с помощью лямбда-выражения, ничем не отличается от функции созданной посредством define, за исключением того, что она не имеет имени.

Фактически - (define (f x₁…x_n)  expr)

полностью эквивалентно - (define  f (lambda (x₁…x_n) expr) ).

Например, sqr можно было бы определить и так

(define sqr (lambda (x) (* x x)))

Получается, что название переменной, связанное с –выражением означает функцию!

Лямбда-выражение может использоваться всюду, где используется имя функции, например как оператор в комбинации вида. Конкретное значение для списка параметров списка, задается после  выражения.

Примеры. Запишем для интерпретации на LISPе выражение (y.(y + 1)) 2

> ((lambda (y) (+ y 1)) 2) 3

Теперь посмотрим на запись примера 2: (x. ( f.f(f x) ) (y.(y + 1)) ) 2

> ((lambda (x) ((lambda (f) (f (f x))) (lambda (y) (+ y 1)) )) 2)

4

Заметим, что интерпретация выражения происходит сразу же, надо только правильно вписать в выражение конкретное значение для связывания.

3.5.2 Функция let и локальное -связывание

Чтобы упростить запись выражений, некоторым его частям можно присвоить локальные имена с помощью связывающий формы let.

(let ((x₁ expr₁)(x₂ expr₂) … (x_n expr_n)) expr)

Его действие таково.

1. Сначала каждое x_i заменяется значением выражения expr_i.

2. Эти значения подставляются в expr

3. Значением всей формы будет значение выражения expr.

Этой формы записи нет в стандартном LISPе, но она полезна и может быть использована при решении лабораторных работ.

Например, функция для вычисления площади треугольника по формуле Герона, а именно: , где 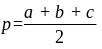без -функции запишется так

>(define (square-triangle1 a b c)

(let ((p (/ (+ a b c) 2)) )

(sqrt (* p (- p a) (- p b) (- p c))) ))

Тело функции получает выражение подобное такому:

(let (p expr_p) expr)

Теперь проверим его работу

> (square-triangle1 5 4 3)

6

Здесь сначала вычисляется значение полупериметра, затем внутренний параметр p связывается с этим полупериметром, что и подставляется в подкоренное выражение.

Заметим, что sqrt – функция встроенная.

Того же эффекта можно было бы добиться применяя лямбда-выражение, но надо предвидеть, их здесь два: для внутреннего параметра p оно своё.

>(define square-triangle2 (lambda (a b c)

(lambda (p) (sqrt (* p (- p a) (- p b) (- p c) )))

(/ (+ a b c) 2) ) )

> (square-triangle2 5 4 3)

6

Результат получается одинаковым, но запись с let как-то привычнее.

Page 16 of 16