3.3 Списки. Часть II

Одна из полезных структур, которые можно создавать с помощью точечных пар – это последовательность. Конечно, последовательности можно представлять в виде пар разными способами. Например, последовательность чисел 1, 2, 3, 4 можно написать в виде пар как

((1.2).(3.4))

или (((1.2).3).4)

или (1.(2.(3.4)))

Но одна последовательность из этих чисел имеет особенное значение, а именно:

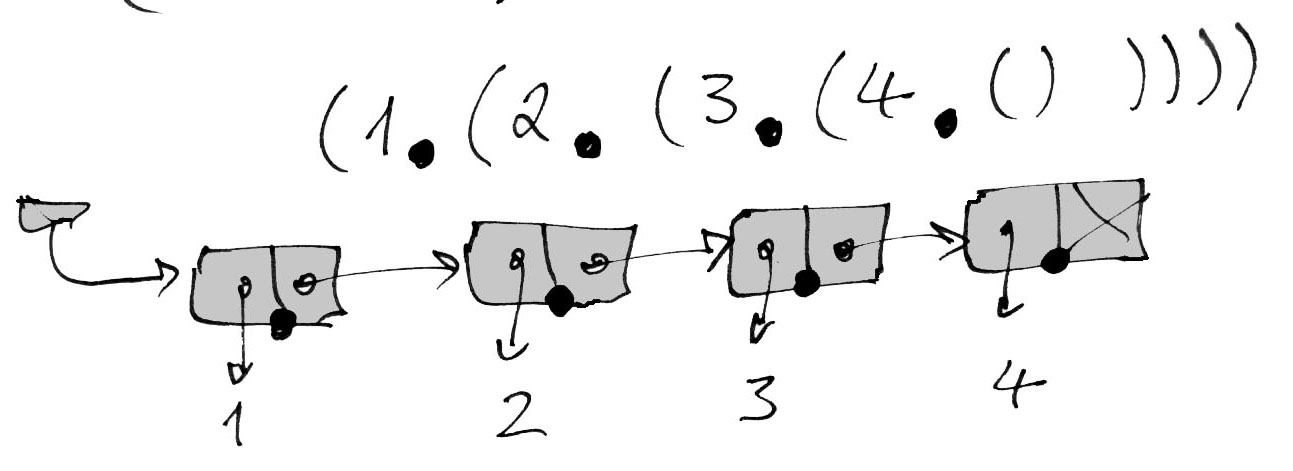
(1.(2.(3.(4.() ))))

Графически это будет выглядеть так:

Здесь первый элемент каждой написанной пары представляет собой соответствующее значение, а второй – записывается как очередная точечная пара со скобкой, но так, что второй элемент самой внутренней, последней пары представляет собой пустой список (по-другому - NIL).

Вот такая организация данных на самом деле и даёт структуру, называемую списком. Это – основа представления всех данных в LISPе

Попробуем получить эту интересную последовательность. А как? С помощью cons!

Почему вместо:

()

можно написать:

‘()

И это будет правильно ???

> (cons 1 (cons 2 (cons 3 (cons 4 () ))))

( 1 2 3 4)

У нас получился классический список. Стоит снова дать определение, но сначала сделаем замечание.

В ыражения вида

(x₁ .(x₂ .( … .(x_n . x_n+1)…))

обычно записывается проще, выбрасыванием как бы два «склеенных» символа «.(», а именно:

(x₁ x₂ … x_n . x_n+1)

Тогда точка остается с последним элементом. Но если элемент x_n+1 представляет собой NIL - то его можно не писать и, тогда выражение получается в виде обычного списка:

(x₁ x₂ … x_n)

А вот теперь определение

Список – это

• либо пустой список,

• либо точечная пара, второй элемент которой является списком.

Итак, получается, что выражение (list a₁ … a_n)

эквивалентно выражению (cons a₁ (cons … (cons a_n () ) … )).

Как вывод: функция cons тоже позволяет получать списки, но действие ее (сравните с list ) таково: новый список состоит из первого списка, за которым следуют элементы второго списка.

> (cons '(1 2) '(3 4)) ===> должно получится((1 2) . (3 4))

((1 2) 3 4)

А вот графическое доказательство этого примера

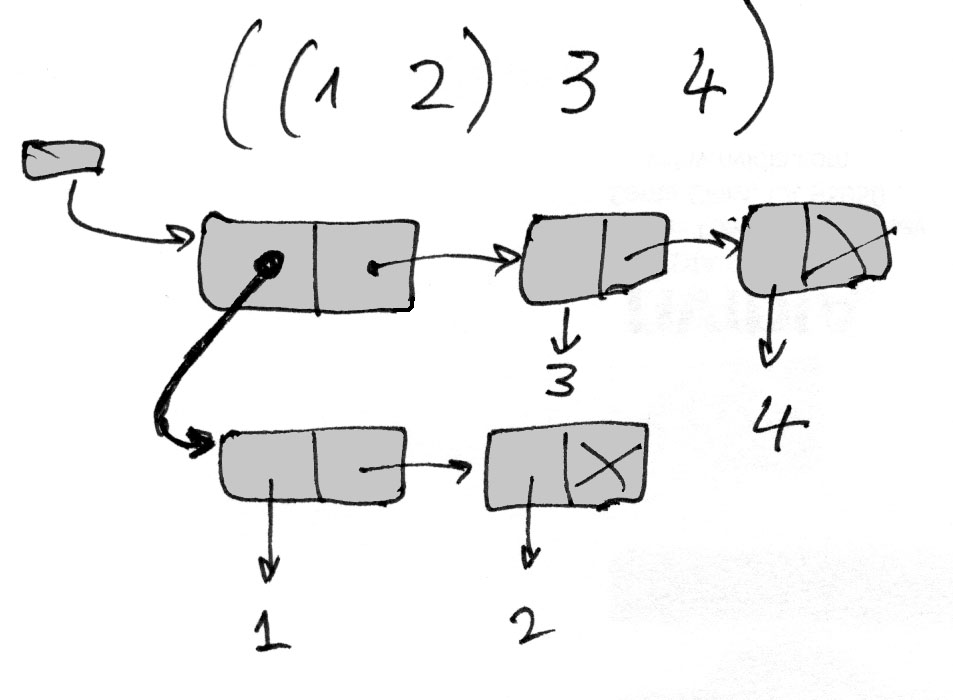
До После

Возникает вопрос: чем различаются действия со списками у функций cons, list и append ?

Если определены два списка (define lst1 '(1 2)) и (define lst2 '(3 4)),

то результаты применения этих функций будут таковы:

1. (list lst1 lst2)  ((1 2) (3 4))

2. (append lst1 lst2)  (1 2 3 4)

3. (cons lst1 lst2)  ((1 2) 3 4)

Существует простой способ добавления нового элемента к списку с помощью cons. Его можно просто поставить в началo уже существующего списка:

> (cons 0 ‘(1 2 3 4))

(0 1 2 3 4)

Чтобы иметь совместимость с примерами функций используемых в других реализациях LISPов, нам придется сделать одно полезное определение - задать пустому списку имя nil.

> (define nil ‘())

> nil

()

Замечание. Значения определения (define nil ‘()) и (define nil ())совпадают.

Теперь просмотрим, как им можно воспользоваться

> (cons 1 (cons 2 (cons 3 (cons 4 nil))))

(1 2 3 4)

3.3.1 Предикат null?

Конечно, обрабатывая список, необходимо отделять случай пустого списка. Встроенный предикат null? и проверяет, является ли его параметр пустым списком.

Примеры.

> (null? ())

#t

> (null? nil)

#t

3.3.2 Предикат list?

Разумеется, нужна процедура, определяющая, является ли данный объект списком. (Правда, эта процедура в Racket есть и является стандартной). Запишем определение предиката, является ли задаваемый аргумент списком:

> (define (list? lst)

(or (null? lst)

(and (pair? lst)

(list? (cdr lst)))))

Этот предикат полностью реализует наше последнее определение списка.

Примеры

> (list? (list 2 3) )

#t

> (list? 2.3)

#f

> (list? ())

#t

3.3.3 Предикат atom?

И, наконец, еще один полезный предикат atom?. Справедливо полагая, что атомом является все, что не есть точечная пара, запишем:

> (define (atom? x)

(not (pair? x)))

> (atom? 1.2)

#t

> (atom? 3)

#t

Вооружившись основными предикатами, напишем две суммирующие функции при работе со списками.