13. Ранг матрицы. Вычисление ранга матрицы с помощью преобразований Гаусса.

Р ангом матрицы является максимальное число линейно независимых строк или столбцов матрицы. Ранг матрицы – максимальный порядок необращающихся в 0 Миноров этой матрицы.

Вычисление ранга матрицы с помощью преобразований Гаусса

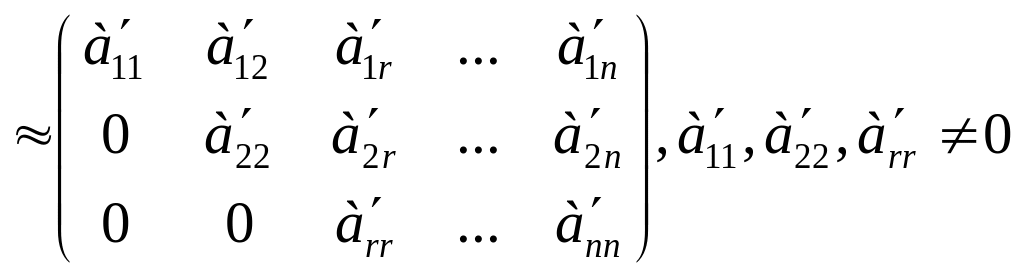
Т к диагональная система векторов всегда является линейно независимой, ранг матрицы (эквивалентные преобразования не меняют ранга матрицы)

1) к строке (столбцу) можно прибавить какую либо строку (столбец), предварительно умножив на какое – либо число

2) Строки (столбцы) можно переставить местами

3) Нулевая строка (столбец) может быть удалена

4) может быть удалена одна из двух пропорциональных строк (столбцов)

14 Вопрос

Система  линейных алгебраических уравнений с неизвестными — это система уравнений вида

Здесь   — количество уравнений, а   — количество неизвестных. x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁,a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными^[1]. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно^[2].

Система (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1) — совокупность n чисел c₁, c₂, …, c_n, таких что подстановка каждого c_i вместо x_i в систему (1) обращает все её уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

Матричная форма

Система линейных уравнений может быть представлена в матричной форме как:

или:

.

Здесь   — это матрица системы,   — столбец неизвестных, а   — столбец свободных членов. Если к матрице   приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.

Основными методами решения элементарных систем линейных уравнений являются метод Крамера, матричный метод и метод Гаусса.. 

15 Фундаментальные системы решений для СЛУ. ФСР - максимальное число линейно независимых решений системы...обычно получаем его когда в системе число переменных больше числа уравнений. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ — “соотношение вида: a1x1 + a2x2 + ... + anxn = 0, где a1, a2, ..., an — числа, из которых хотя бы одно отлично от нуля; x1, x2, ..., xn — те или иные математические объекты, для которых определены операции сложения и умножения на число”38. Термин объясняется тем, что величины x1, ..., xn входят в данное соотношение в 1-й степени, т. е. линейно. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет.

Классификация СЛАУ

1. Если число уравнений больше чем число неизвестных, т.е. n>m, то СЛАУ на-

зывается переобусловленой

2. Если число уравнений меньше чем число неизвестных, т.е. n<m, то СЛАУ на-

зывается недообусловленой

3. Если число уравнений равно числу неизвестных, т.е. n=m, то СЛАУ называет-

ся нормальной(С) ИиКП РХТУ февраль 2010г. Калинкин Владимир Николаевич 2

4. Если вектор свободных членов равен нулю→ →b = 0 , то СЛАУ называется од-

нородной

5. Если вектор свободных членов не равен нулю→ →b ≠ 0 , то СЛАУ называется не-

однородной

6. Если система, имеет хотя бы одно решение, она называется совместной. Сис-

тема, не имеющая решений, называется несовместной.

7. Совместная система, имеющая единственное решение, называется определен-

ной, а имеющая бесчисленное множество решений, называется неопределен-

ной.

Очевидно, что однородная система всегда совместна, так как имеет хотя бы од-

но решение→ → x = 0 , которое называется тривиальным

___________________________________________________________________________________________________________________________________