Проверочный расчет цилиндрической передачи на контактную прочность.

Ведется по формуле- σ_H =Z_H Z_м Z_ε √ w_Ht (u+1) / d_w1 u.

Где: а)σ_H-рачетное контактное напряжение [М Па];

б)Z_H= cosβ/ √cosα_tw sinα_w - коэффициент, учитывающий форму сопрягаемых поверхностей.

Здесь α_tw ≈arc tg (tgα _w / cosβ) - угол зацепления в самом общем случае. При α=20⁰ и Х_Σ=0 значение

α _w=α; если при этом зубья прямые β=0⁰, то коэффициент Z_H=1,76;

в)Z_м= √2Е₁ Е₂ /π [ Е₁ (1-μ₂²)+ E₂(1-μ₁²)]-коэффициент, учитывающий механические свойства материалов зубчатых колес (модуль упругости и коэффициент Пуассона). Если шестерня и колесо стальные, можно принять Z_м=√0,35 E [М Па];

г)Z_ε-коэффициент, учитывающий суммарную длину контактных линий. Для прямозубых колес в фазе однопарного зацепления Z_ε=1, для косозубых Z_ε=√1/ K ε_α. См. приложения№8 и №1;

е)w_Ht=F_t1 К_Hα К_Hβ К_Hv / b_w [Н мм]- удельная расчетная окружная нагрузка на зубья. Здесь

F_t1=F_n cos α =2 M_1р / d_w1 [Н ]-окружная сила; значения коэффициентов К_Hα и К_Hβ см. выше.

К_Hv=1+w_Hv b_w / F_t1 = 1+b_w1(δ_H g₀ V √а_w /u) / F_t1-коэффициент, учитывающий дополнительную динамическую нагрузку, возникающую вследствие погрешностей по шагу зацепления и зависящий от ряда факторов. Коэффициент δ_H учитывает вид зубьев, твердость их поверхности и модификацию, которая выполняется на ведомых колесах в виде фаски у вершины зубьев и назначение которой -увеличение площади при вхождении в контакт с основанием зубьев ведущего колеса. См. приложение №10. Коэффициент g₀ учитывает погрешности по шагу у шестерни и колеса, зависит от модуля и степени выбранной точности изготовления. См. приложение №11(если значение нагрузки

W _Hv = δ_H g₀ V √а_w / u ≤W_v , дополнительно возникающей вследствие погрешностей по шагу, превысит предельное значение W_v , то следует принять W_HV =W_V )

Для решения вопроса о прочности зубчатого зацепления необходимо сравнить полученное расчетное контактное напряжение с допускаемым контактным напряжением, т.е. проверить условие прочности

σ_H ≤ σ_Hр.

Если условие прочности не соблюдается, необходимо увеличить модуль, т.е. увеличить размеры ЗК и снизить контактные напряжения. Расчет повторить.

Особенности расчета на прочность конических зубчатых передач.

Из-за сложности изготовления с высокой

точностью, неравномерности распределения нагрузки по ширине зубьев, возникновению осевой силы, а так же необходимостью регулирования взаимного расположения зубчатых колес при монтаже, несущая способность конических передач примерно на 15% ниже, чем у цилиндрических.

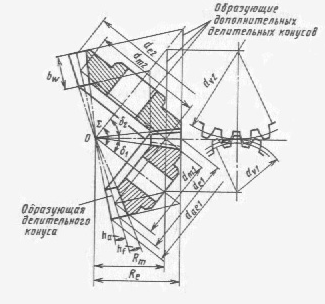
Порядок проведения проектировочных и проверочных расчетов, большая часть вводимых коэффициентов, а т.ж. величина предельных и допускаемых напряжений такие же, как у цилиндрических ЗК. Поэтому рассмотрим только те формулы и значения, в которых имеются отличия, связанные с формой зубчатых венцов. В зависимости от величины угла Σ, под которым пересекаются оси конических ЗК, передачи делятся на ортогональные, когда Σ=δ₁+δ₂=90º (рис.1.15) и не ортогональные, когда Σ=δ₁+δ₂≠90˚. Здесь δ₁ и δ₂- половинные углы при вершинах делительных конусов ЗК. На рисунке показаны конические колес у которых модуль меняет свою величин по ширине зуба и соответственно изменяется высота зубьев. Рис.1.15.

По аналогии делительной окружностью цилиндрических колес у конических ЗК имеется делительный конус -R_e , а т.ж. конус впадин и конус вершин. На рис.1.15. показаны ЗК с пропорционально понижающейся формой зубьев, т.е. когда вершины делительного конуса и конуса впадин совпадают. Толщина зуба и ширина впадин увеличиваются пропорционально расстоянию от

в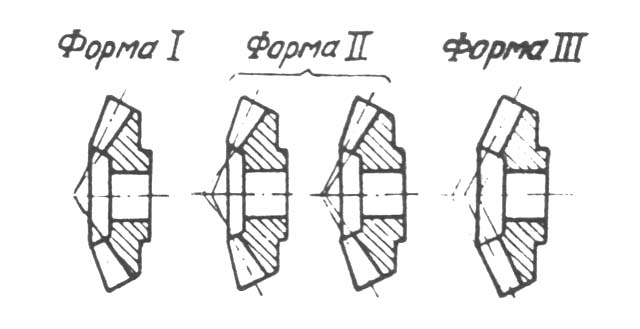 ершины конусов (см. рис.1.16 форма 1). Эта форма является основной для прямозубых и косозубых ЗК. Для колес с круговыми зубьями чаще применяется форма 2 с понижающимися зубьями, при которой вершины конусов не совпадают,

толщина зубьев растет, а ширина впадин

остается постоянной. Форма 3 равновысокими зубьями, при которой образующие конусов вершин, впадин

и делительного параллельны, так же

чаще используется при круговых зубьях

(см. рис 1.16.).

Рис.1.16.

Ширину зубчатого венца -b_w измеряют по образующей делительного конуса. Эвольвентная форма зубьев получается на развертке дополнительных конусов, образующие которых перпендикулярны образующей делительного конуса. Параметраы зубьев в таких сечениях имеют индекс t (торцевые). Выделяют три торцевых сечения: внешнее с индексом t_e; среднее t_m; внутреннее t_i. Соответственно имеем внешнее –R_e и среднее –R_m делительные конусные расстояния, а т.ж. внешний–m_te и средний–m_tm торцевые модули. Делительные диаметры в соответствующих сечениях (см. рис.1.14) можно определить из соотношений: d_e=m_te z; d_m=m_tm z; m_tm=m_te (1-0,5Ψ_R). Где z-число зубьев, а Ψ_R=b_w / R_e - относительная ширина ЗК принимается в пределах 0,1-0,3.

Для колес с прямыми зубьями стандартизован внешний торцевой модуль m_te, с конусным расстоянием он связан соотношением: m_te=2R_e sinΣ / √z₁²+z₂² +2z₁ z₂ cosΣ [мм].

Конусное расстояние определяется с помощью проектировочной формулы:

R̃_e ≥ 0.82 (√ u²+1+2u cosΣ / ³√u sin²Σ) ³√ М_1р E K_Hα K_Hβ K_Hv f(β) / σ²_Hр Ψ_R (1-0,5Ψ_R)² [мм].

Где: u=d_m2 / d_m1=z₂/z₁=sinδ₂ / sinδ₁ - передаточное число конической передачи. При Σ=90⁰ получаем u=tgδ₂=ctgδ₁, при Σ>90⁰ нужно учитывать перемену знака у cosΣ;

f(β)=cos²β /k ε_α - функция от угла наклона зубьев в среднем сечении, при прямых зубьях f(β)=1;

Все остальные коэффициенты вычисляются и или принимаются так же, как и для цилиндрической передачи (см. выше), и подставляются в проектировочную формулу. Полученный результат используется для получения приближенного значения внешнего торцового модуля

m̃_te =2Re sinΣ /√(z ₁²+z ₂²+2z₁ z₂ cosΣ) [мм].

Полученное приближенное значение приводится к стандартному значению модуля и производится расчет основных размеров конических ЗК,входящих в передачу:

внешних делительных диаметров шестерни и колеса d_e1=m_te z₁, d_e2= m_te z₂ с точностью до 0,01;

точного значения конусного расстояния Re=(m_te / 2sinΣ )√(z ₁²+z ₂²+2z₁ z₂ cosΣ) с точностью до 0,01мм

рабочей ширины зубчатых венцов b_w=Ψ_R Re(m_tm /m_te) с точностью до 0,01мм;

половинных углов при вершинах делительных конусов δ₁=arc sin(0,5 d_e1/Re) и δ₂=Σ-δ₁ с точн. до 2".

Конструкция зубчатых колес.

Основными конструктивными элементами ЗК. являются (см. рис.1.17): 1- зубчатый венец (включающий в себя зубья–1 и обод-1); 4-диск; 2-ступица; 3-фланец (в том случае, если из-за большого размера и ширины зубчатый венец изготовляется отдельно и прифланцовывается к диску, выполненному совместно с валом). Для нахождения формы и размеров, названных частей необходимо перейти на более высокий уровень эскизного проекта и рассмотреть ЗК во взаимодействии с другими элементами передачи, прежде всего с валом, на котором оно установлено. Принципы проектирования вала будут изложены в следующем разделе, а сейчас рассмотрим основные рекомендации по конструированию ЗК.

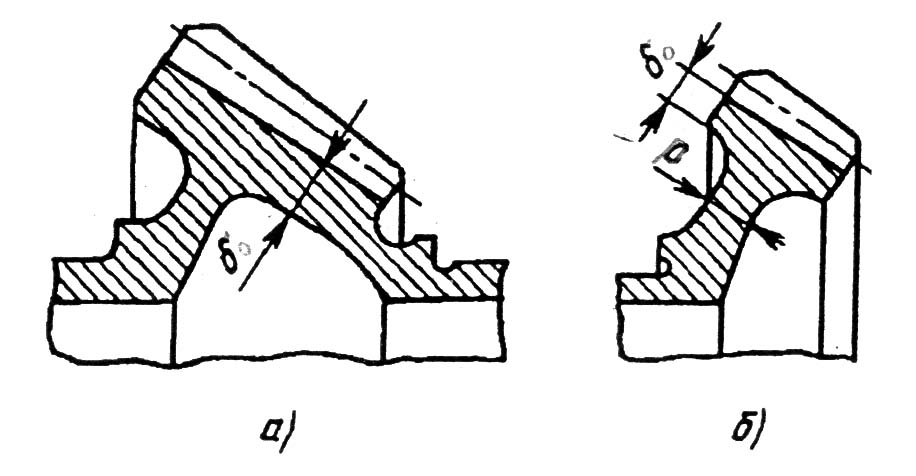
Обод должен быть достаточно жестким, чтобы при нарезке зубьев не происходило искажения их профиля, в то же время податливым, чтобы способствовать выравниванию нагрузки по ширине зубьев. Для цилиндрических ЗК можно принять δ=(1,7-2,0)m. В широких ЗК большого диаметра для увеличения жесткости на консольной части диска выполняют бурты, а промежутки делают тонкими для снижения веса; можно принять δ=(1,4-1,6)m , δ=(2,2-2,5)m и S ≥δ. У конических колес обод чаще всего очерчивается конической же поверхностью соосной с поверхностью впадин δ₀=(2-3)m_te.

Диск ЗК соединяет зубчатый венец со ступицей, критерием его работоспособности при выборе толщины является жесткость. Для снижения веса в диске растачиваются отверстия. Зубчатый венец цилиндрических колес желательно располагать симметрично относительно диска, иначе в последнем возникает изгибающий момент. Для цилиндрических ЗК можно принять p=(0,2-0,3)b; для прифланцовываемых ЗК с малой и средней твердостью зубьев p=(0,08-0,12)b; в случае применения цементации зубьев толщину диска выбрают

p=(0,12-0,25)b.В конических и косозубых колесах дискам можно придать колоколообразную форму для уменьшения изгибающих нагрузок (см. рис.1.18).

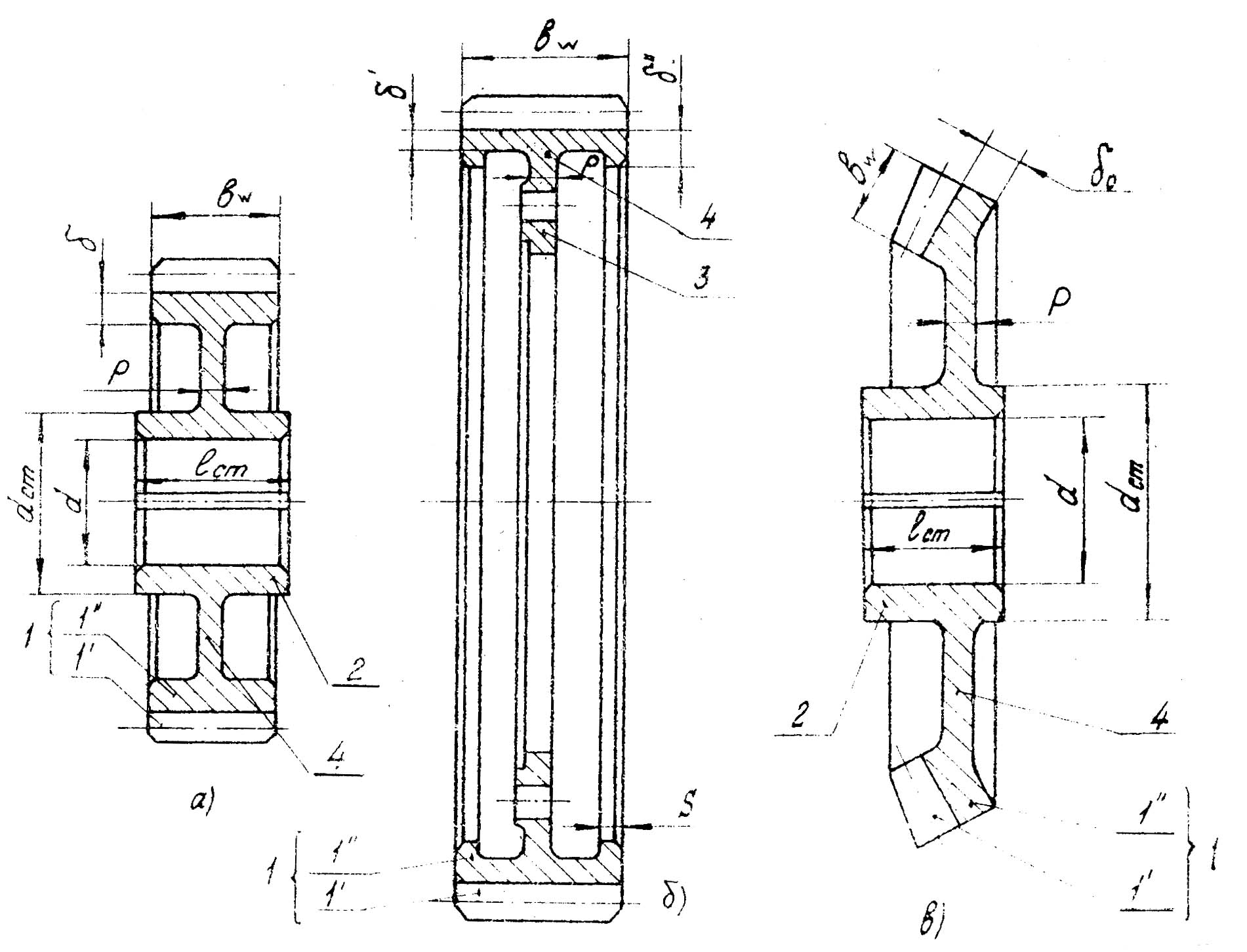
Рис.1.17.

Ступица- это элемент соединяющий колесо с валом. При одинаковых материалах, из которых изготовлены вал и ступица, а так же в случае небольшого отличия в их размерах d_f ≤ (2,5-2,0) d_в целесообразно нарезать зубчатое колесо на валу (см. рис.1.18. и 1.25.). Особенности нарезания ЗК на валах см. приложение №12. Снижение уровня взаимозаменяемости компенсируется высокой точностью расположения зубьев относительно цапф вала (поверхностей, на которые устанавливаются подшипники), прочностью, надежностью, технологичностью и небольшим весом.

Колеса делаются насадными, если материалы ЗК и вала различны; если из-за большой разницы в диаметрах много заготовок, выполняемых штамповкой или поковкой, идет в брак; если этого требуют условия монтажа и т.п. В этом случае в ступице должны быть выполнены поверхности, обеспечивающие передачу крутящего момента и точное расположение (центрирование) зубчатого колеса относительно вала. Рекомендуемые размеры ступицы d_ст =(1,1-1,5) d и l_ст =(0,8-1,5) d выбираются в зависимости от условий нагружения и способа установки ЗК на валу. Рассмотрим некоторые из них.

Рис.1.18.

Шпоночное соединение – соединение с помощью шпонки вала и надетой на него детали. Шпонка (от нем. Spon, Span –щепка, клин) это деталь чаще призматической формы, которая вставляется в соответствующий паз в ступице и на валу (см. рис.1.19.а).Она стандартизована и подбирается в зависимости от диаметра вала d_в ≥ 6мм (см. приложение №13). Длина шпонки расчитывается и округляется до ближайшего стандартного размера При меньших размерах вала d_в≥3мм и меньших нагрузках можно применить сегментную шпонку (см. рис.1.19.б и приложение№13). Паз в ступице выполняется протяжкой или менее точно, долблением если HB>380-400, паз на валу выполняется фрезерованием пальчиковой или дисковой фрезами (см. рис.1.20.). Для удобства сборки в паз вала шпонка устанавливается с легким натягом P9/h9 или N9/h9, а в паз втулки с зазором J_s9/h9 или H9/h9. Точное центрирование ЗК на валу обеспечивается переходной посадкой H7/k6.

Проверку прочности стандартного соединения проводят по напряжению смятия:

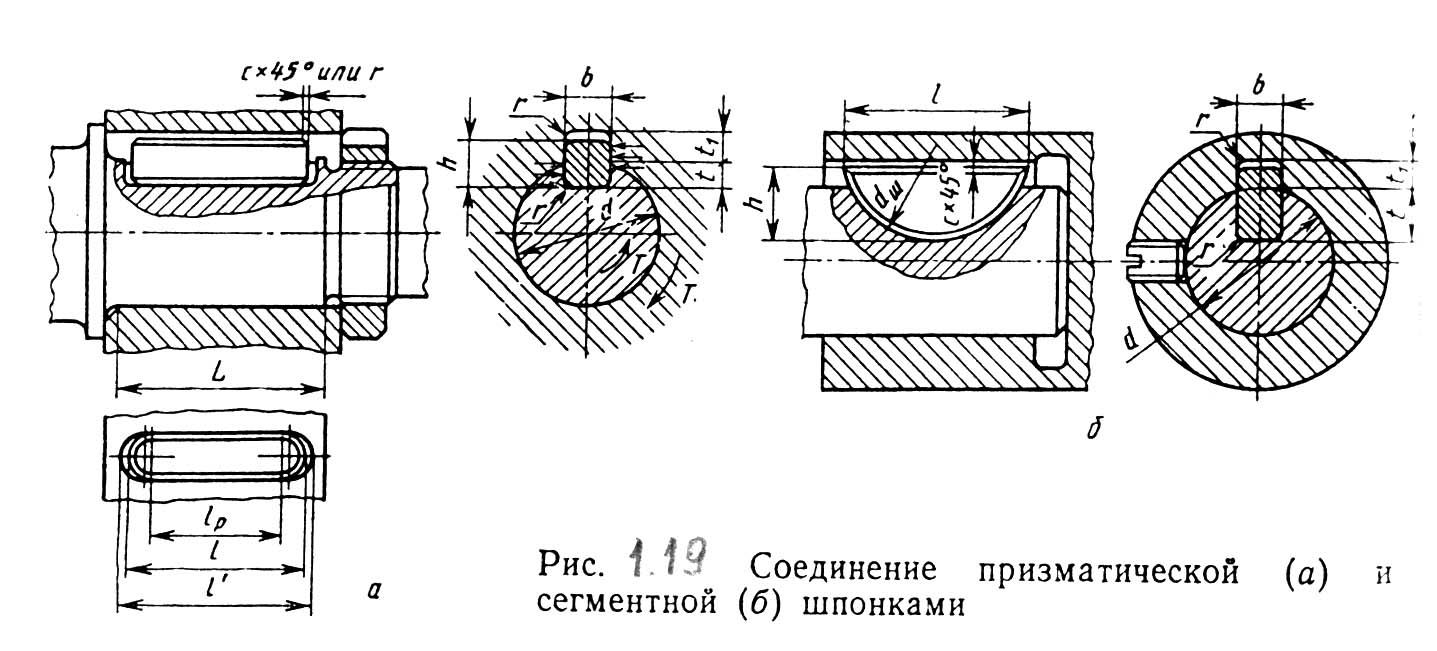σ_см=2М/d (h-t) l_р ≤ [σ_см] . Где: М-расчетный крутящий момент; d-диаметр вала; h-высота шпонки; t≈0,4 h –глубина паза на валу;l_р-рабочая длина шпонки; [σ_см]=σ_т / [n]-допустимое напряжение смятия.

П редел текучести для чистотянутой стали 45 - σ_т=350 М Па, для ст. 30ХГСА –850 М Па. Допустимый запас прочности зависит от условий нагружения: [n]=1,9-2,3 при нереверсивной спокойной нагрузке; [n]=2,9-3,5 при нереверсивной с частыми остановками и пусками; и запас прочности повышается ещё на 30% при реверсивных режимах работы.

Достоинство шпоночных соединений в том, что они просты и дешевы в изготовлении и эксплуатации, легко монтируются и разбираются. Стандартные шпонки изготавливаются из чистотянутых калиброванных прутков.

Недостатком является концентрация напряжений на валу и в ступице; невысокая

Рис.1.20. несущая способность, которую невозможно увеличить за счет увеличения числа шпонок, т.к. не удастся добиться точного взаимного расположения пазов и, следовательно, равномерной загрузки; в высокооборотных механизмах создается дисбаланс.

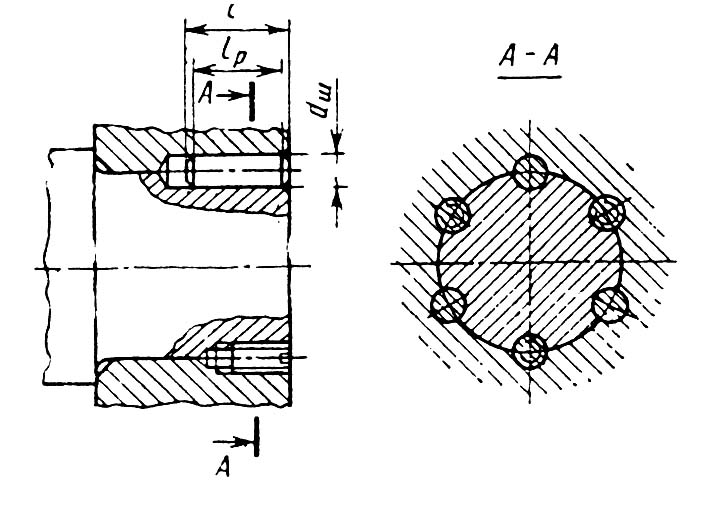В авиационных механизмах широкое распространение получили соединения с цилиндрическими шпонками (штифтами) (см. рис.1.21). Деталь устанавливается на валу с легким натягом H7/p6 или H7/k6, затем в стыке сопрягаемых поверхностей сверлятся и обрабатываются разверткой отверстия, в которые с натягом устанавливаются штифты H7/u8 или P7/h6. Для достижения осевой фиксации насадной детали в части отверстий

нарезается резьба и устанавливаются винты, головки которых срезаются, а оставшаяся часть раскернивается для обеспечения стопорения. Совместная обработка вала и ступицы позволяет добиться равнозагруженности всех устанавливаемых шпонок, а с

Рис.1.21. учетом меньшего ослабления вала и ступицы отверстием круглой формы, несущая способность такого соединения очень высокая. Проверка на прочность осуществляется по формуле: σ_см=4М/d d_ш l_р n ≤ [σ_см] . Где: n-число гладких штифтов. К недостаткам следует отнести снижение уровня взаимозаменяемости, т.к. соединение неразборное, и не всегда выполнимое из-за сложностей связанных с подходом инструментами.

Для валов размерами менее 3мм, а так же в случае передачи малых усилий применяется радиальное штифтовое соединение (См. рис.1.22). Отверстие под штифт выполняется после установки детали на валу и поэтому считается неразборным. Для предохранения от выпадения в торцевой части штифтов делают кернение или расчеканивание. Вал сильно ослабляется отверстием, поэтому диаметр стандартного штифта выбирается в интервале d_ш =(0,2-0,3)d. Основными разрушающими факторами считаются срез и смятие, поэтому проверка на прочность ведется по формулам: τ_ср=M / d π d_ш²≤ [τ_ср] и σ_см=2М/ d (d_ст-d) d_ш ≤ [σ_см]. Можно принять [τ_ср ]≈0,6[σ_см]. Размеры цилиндрических стандартных штифтов приведены в приложении №14.

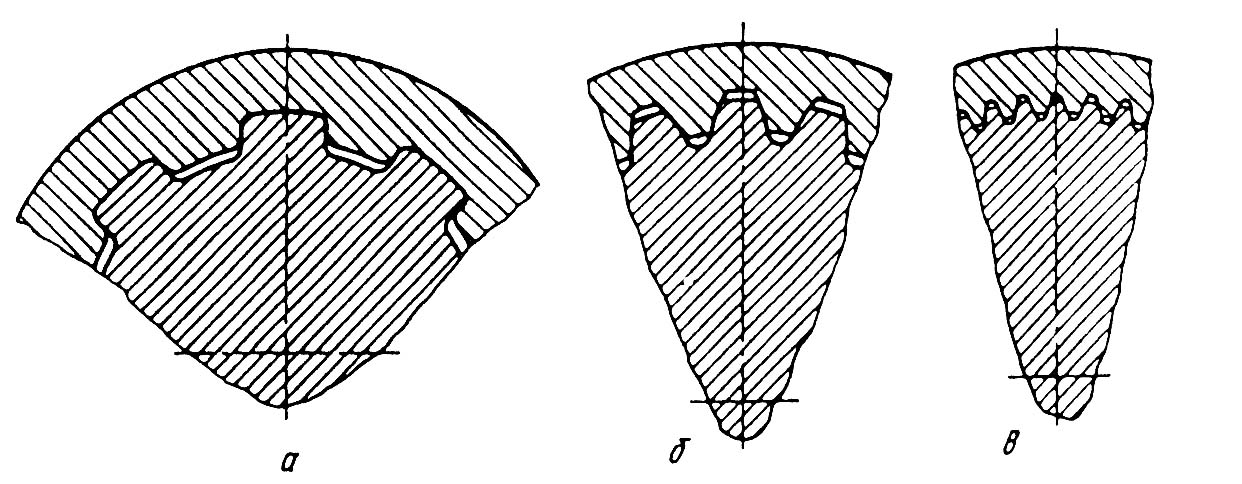
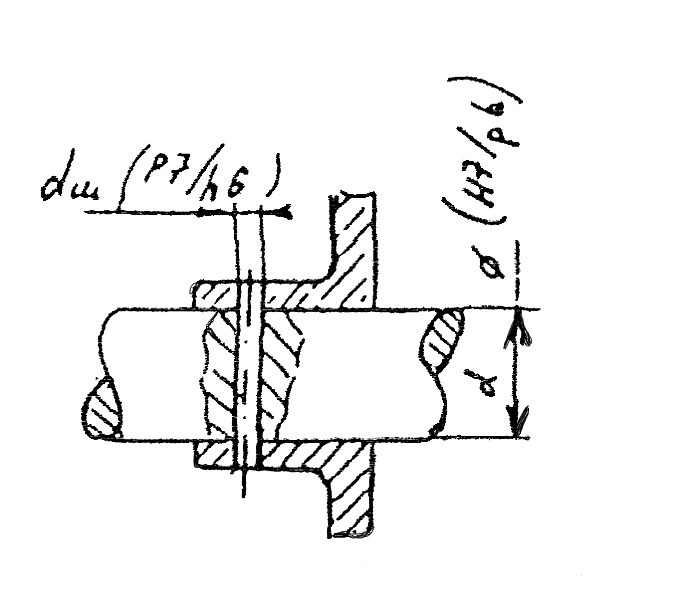
Рис.1.22. Рис.1.23.

Шлицевое соединение – соединение двух деталей с равномерно расположенными пазами и выступами. Выступы могут иметь эвольвентный, прямобочный и треугольный профиль (см. рис.1.23). Наибольшей несущей способностью обладают эвольвентные шлицы, т.к. имеют больший угол у основания шлица. Если в ступице отсутствуют специальные центрирующие поверхности, эту функцию можно выполнить точно изготовленными поверхностями зубьев. На рис.1.24. показано центрирование по наружному диаметру а) и г), по внутреннему диаметру б) и д), по боковой поверхности шлицев в) и е).

Если пазы в ступице калибруются протяжкой (HB<350), предпочтительно центрирование по наружному диаметру, т.к. на валу сопрягаемую поверхность шлицев можно обработать шлифованием. Если пазы в ступице вырезаются долбяком (при HB>350), целесообразно выбрать в качестве центрирующей поверхности внутренний диаметр. Центрирование по боковым поверхностям обеспечивает более равномерное распределение нагрузки по шлицам, поэтому предпочтительно для тяжело нагруженных реверсивных соединений. При прямобочных шли-

Рис.1.24. цах такое центрирование можно применять только при использовании протяжки.

Основной разрушающей нагрузкой для шлицевого соединения является смятие и расчет ведется по формуле: σ_см=2М/ d_m z h l ψ≤[σ_см]. Где для прямобочных:d_m=(D+d)/2; h=(D-d)/2 –2f; f-зазоры и скругления. Для эвольвентных: d_m=mz ; h=0,9 m. Число зубьев –z, коэффициент учитывающий неравномерность распределения нагрузок на шлицах в зависимости от точности изготовления ψ=(0,7-0,8). Допустимое напряжение смятия -[σ_см]. в большой степени зависит от характера посадки и изменяется от 35[М Па] для подвижных, до 200[М Па] для установленных с натягом. Для неподвижных, работающих в условиях вибраций можно принять [σ_см]≈80[М Па]

Шлицевые соединения технологичны, легко монтируются и разбираются, обладают высоким уровнем взаимозаменяемости. Несущая способность шлицевых соединений выше, чем соединений с призматической шпонкой, его применение целесообразно при полых валах. Размеры и число зубьев выбираются в зависимости от номинального диаметра вала (см. приложения №15 ), о конструктивных особенностях шлицевых участков вала можно узнать из приложения №16.

Окончательный выбор конструкции зубчатых колес не может быть сделан без учета конструкций валов или осей на которых они устанавливаются .