Ііі частина (3 бали)

Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.

8. Доведіть, що коли площина перетинає площину трапеції по прямій, яка містить її середню лінію, то вона паралельна основам трапеції.

Варіант 3

І частина (5 балів)

Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Оберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.

1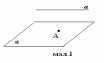 . Скільки спільних точок має площина α і площина, яка проходить через точку А і пряму а (мал. 1)?

А) одну; Б) дві;

В) безліч; Г) три.

2. Якою фігурою може бути паралельна проекція квадрата на площину?

А) трикутником; Б) трапецією;

В) паралелограмом; Г) точкою.

3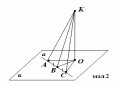 . На мал. 2 КО   α, ОВ   а. Порівняйте довжини відрізків КА і КС.

А) КА < КС; Б) КА = КС;

В) КА > КС; Г) не можна визначити.

4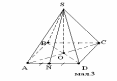 . На мал.3 зображено правильну чотирикутну піраміду SABCD. SO  висота. Який градусна міра кута між площинами SOA і SOD?

А) 45°; Б) 30°;

В) 60°; Г) 90°.

5. Ортогональною проекцією многокутника площею S = 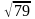 є многокутник площею S₁. Яке з чисел не може бути значенням параметра S₁?

А) 3; Б) 5; В) 7; Г) 9.

Іі частина (4 бали)

Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами

6. Катет прямокутного трикутника дорівнює 30 см, а гіпотенуза відноситься до другого катету як 17 : 8. Знайдіть сторони трикутника.

7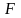 . Побудуйте переріз прямої призми ABCDA₁B₁C₁D₁ площиною, що проходить через вершини С, D₁ та точку F на ребрі АА₁.

Ііі частина (3 бали)

Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.

8. Дано трикутник АВС, в якому АВ = 16 см, АС = 12 см, ВС = 20 см. На стороні АВ взято точку М так, що ВМ : МА = 3 : 1. Через точку М проведено площину, яка перетинає сторону АС в точці К. Знайдіть площу трикутника АМК, якщо відомо, що дана площина паралельна ВС.

Варіант 4

І частина (5 балів)

Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Оберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.

1. Дано дві прямі a і b , що перетинаються. Через точку А, яка лежить на прямій а, проведено пряму с паралельно прямій b. Скільки різних площин можна провести через ці три прямі?

А) одну; Б) дві; В) три; Г) жодної.

2. Якою фігурою може бути паралельна проекція прямокутника на площину?

А) трикутником; Б) трапецією; В) відрізком; Г) точкою.

3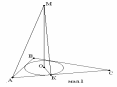 . На мал.1 точка О-центр вписаного в трикутник АВС кола, ОМ   (АВС), ОК   АС. Відстані від точки М до точок А і К дорівнюють a і b відповідно. Порівняйте величини a і b, якщо це можливо.

А) 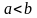; Б) ;

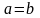В) 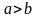; Г) порівняти неможливо.

4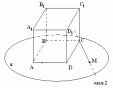 . Точка М належить площині грані АВСD прямокутного паралелепіпеда АВСDA₁B₁C₁D₁ (мал. 2). Знайдіть кут між прямими A₁В₁ і СМ, якщо кут ВСМ дорівнює 140º.

А) 40°; Б) 50°;

В) 90°; Г) 140°.

5. Площа проекції чотирикутника дорівнює 24 см². Кут між площиною проекції та площиною даного чотирикутника становить 60°. Знайдіть площу чотирикутника.

А) 48 см²; Б) 18 см²; В) 20 см²; Г) 62 см².