
- •Федеральное агентство по образованию
- •Исследование операций
- •Содержание
- •Введение
- •Лабораторная работа 1 Метод численного моделирования (Метод Монте-Карло)
- •Общие сведения
- •Моделирование случайных величин с равномерным распределением в интервале [0; 1]
- •Псевдослучайные числа
- •Алгоритмы генераторов псевдослучайных чисел
- •Линейный конгруэнтный метод (лкм)
- •Алгоритм Вичманна–Хилла (Wichmann–Hill или as183)
- •Алгоритм «Виток Мерсенна» (Mersenne Twister или mt19937)
- •Алгоритм Парка−Миллера (Park, Miller)
- •Метод Фибоначчи с запаздыванием
- •Функция random() в различных приложениях
- •Оценка точности результатов, полученных методом Монте-Карло
- •Лабораторное задание
- •Контрольные вопросы
- •Цель работы: научиться моделировать случайные величины с заданным законом распределения
- •Моделирование случайных событий
- •Моделирование непрерывной случайной величины
- •Алгоритмы моделирования некоторых типов случайных величин Экспоненциальное распределение
- •Пуассоновская случайная величина Распределение вероятностей числа событий на интервале времени для пуассоновской св с параметром определяется выражением
- •Гауссовская случайная величина
- •Случайная величина с логнормальным распределением
- •Моделирование n-мерной случайной величины
- •Варианты заданий для лабораторной работы 2
- •Контрольные вопросы
- •Цель работы: научиться определять основные характеристики системы массового обслуживания с помощью метода численного моделирования
- •Потоки событий
- •Многоканальная смо с ожиданием
- •Основные характеристики смо
- •Моделирование систем массового обслуживания
- •Лабораторное задание
- •Контрольные вопросы
- •Рекомендуемая литература
- •Алгоритм «Виток Мерсенна» (реализация алгоритма на языке с)
- •Результаты тестирования датчиков случайных чисел
- •Критерий согласия хи-квадрат Пирсона
Случайная величина с логнормальным распределением
Плотность вероятности СВ с логнормальным распределением имеет вид:
![]() . (18)
. (18)
Здесь
параметры
![]() и
и
![]() равны среднему и дисперсии
равны среднему и дисперсии
![]() .
При этом математическое ожидание
и дисперсия
.
При этом математическое ожидание
и дисперсия
![]() равны
равны
![]() ,
,
![]() .
.
Если
![]() имеет нормальное распределение с
параметрами
имеет нормальное распределение с
параметрами
![]() и
и
![]() ,
то СВ
,
то СВ
![]()
имеет логнормальное
распределение с параметрами
![]() ,
средним
,
средним
![]() и дисперсией
и дисперсией
![]() .
.
Таким образом, моделирование СВ с логнормальным распределением можно свести к моделированию гауссовской СВ с , и последующему преобразованию
![]() .
.
При этом
![]() ,
,
![]() .
Если заданы
среднее
и
дисперсия
СВ
с логнормальным распределением, то ее
значение можно найти с помощью линейного
преобразования
.
Если заданы
среднее
и
дисперсия
СВ
с логнормальным распределением, то ее
значение можно найти с помощью линейного
преобразования
![]() . (19)
. (19)
Моделирование n-мерной случайной величины
Рассмотрим
непрерывную n-мерную
СВ
![]() с совместной плотностью вероятности
с совместной плотностью вероятности
![]()
Для ее моделирования
сначала разыгрывают значение
![]() СВ
СВ
![]() .
Это значение берется в качестве аргумента
условной плотности вероятности
.
Это значение берется в качестве аргумента
условной плотности вероятности
![]() ,
и разыгрывается значение
,
и разыгрывается значение
![]() СВ
СВ
![]() .
Значения
.
Значения
![]() берутся в качестве аргументов условной
плотности вероятности
берутся в качестве аргументов условной
плотности вероятности
![]() и т. д.
и т. д.
Лабораторное задание
Реализовать на ЭВМ алгоритм моделирования СВ с заданной плотностью вероятности. Параметры распределений задать самостоятельно. Величину константы определить из условия нормировки.
Получить выборку размером и построить по ней гистограмму, найти оценки среднего и дисперсии СВ, сравнить их с точными значениями. Определить величину относительной среднеквадратической погрешности полученных оценок.
В заданиях, где это указано, по критерию согласия Пирсона (см. приложение 4) определить меру отклонения исходной плотности вероятности и полученной гистограммы.
Оформить в электронном виде отчет по результатам лабораторной работы, включив в него: цель работы, алгоритм моделирования заданной СВ и результаты расчетов. Также отчет должен содержать обсуждение полученных результатов.
Варианты заданий для лабораторной работы 2
СВ с логнормальной плотностью вероятности (18). Выполнить задание 3.
Реализовать три алгоритма моделирования гауссовской СВ и по критерию согласия Пирсона сравнить их эффективность.
Пуассоновская СВ (14). Выполнить задание 3.
СВ с биномиальным распределением вероятностей:
![]() ,
,
где
![]() –
число сочетаний из
по
;
–
число сочетаний из
по
;
![]() ,
,
![]() .
Выполнить задание 3. При моделировании
СВ учесть, что биномиальное распределение
является моделью случайных экспериментов,
состоящих из
независимых однородных испытаний,
в
каждом из которых вероятность
положительного исхода равна
.
.
Выполнить задание 3. При моделировании
СВ учесть, что биномиальное распределение
является моделью случайных экспериментов,
состоящих из
независимых однородных испытаний,
в
каждом из которых вероятность
положительного исхода равна
.
СВ с плотностью вероятности:
![]()
Выполнить задание 3.
СВ с плотностью вероятности:
![]()
Выполнить задание 3.
СВ с плотностью вероятности (распределение Лапласа или двойное экспоненциальное распределение):
![]()
Выполнить задание 3.
СВ с плотностью вероятности:

где
,
![]()
![]() – параметры распределения. Выполнить
задание 3.
– параметры распределения. Выполнить
задание 3.
СВ с плотностью вероятности (распределение Коши):
![]() ,
,
где
![]()
![]() − параметры распределения. Выполнить
задание 3.
− параметры распределения. Выполнить
задание 3.
СВ с плотностью вероятности (распределение Максвелла):
 ,
,
где − параметр распределения. Выполнить задание 3.
СВ
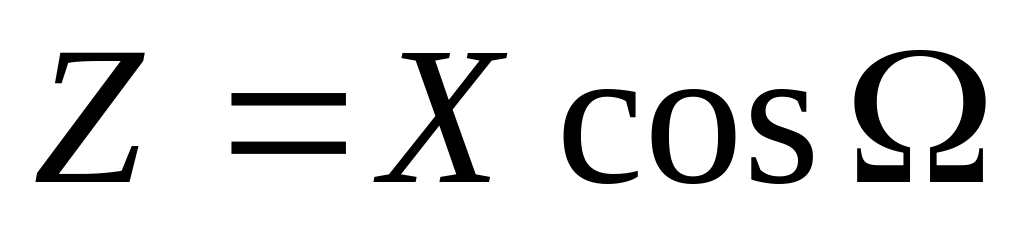 ,
где
и
,
где
и
 независимые случайные величины. СВ
имеет
распределение Релея:
независимые случайные величины. СВ
имеет
распределение Релея:

где
![]() параметр распределения. СВ
имеет равномерное распределение на
интервале
параметр распределения. СВ
имеет равномерное распределение на
интервале
![]() .
Для релеевского распределения выполнить
задание 3.
.
Для релеевского распределения выполнить
задание 3.
Случайная величина
 ,
где
и
независимые гауссовские СВ с различными
параметрами.
,
где
и
независимые гауссовские СВ с различными
параметрами.Случайная величина
 ,
где
и
независимые гауссовские СВ с различными
параметрами.
,
где
и
независимые гауссовские СВ с различными
параметрами.Случайная величина
 ,
где
и
независимые релеевские СВ с различными
параметрами (см. вариант 11).
,
где
и
независимые релеевские СВ с различными
параметрами (см. вариант 11).Случайная величина
 ,
где
независимые случайные величины с
равномерным распределение в интервале
,
где
независимые случайные величины с
равномерным распределение в интервале
 .
При различных
значениях параметра
по критерию согласия
Пирсона (см. приложение 4) определить
степень отклонения полученной
гистограммы СВ
от гауссовской плотности вероятности.
.
При различных
значениях параметра
по критерию согласия
Пирсона (см. приложение 4) определить
степень отклонения полученной
гистограммы СВ
от гауссовской плотности вероятности.
Указания. При
вычислении среднего и дисперсии СВ
![]() можно воспользоваться формулами:
можно воспользоваться формулами:
![]() ,
,
![]() .
.
Также следует учитывать, что для независимых случайных величин и выполняются следующие соотношения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
