Моделирование случайных событий

Рассмотрим полную группу несовместных событий с вероятностями . Разделим интервал [0; 1] на интервалов таких, что длина интервала равна вероятности . В результате получаем рассмотренную выше схему моделирования дискретной случайной величины.

Замечание. Если есть одно случайное событие с вероятностью , то до полной группы событий его дополняет с вероятностью .

Моделирование непрерывной случайной величины

Рассмотрим непрерывную СВ с плотностью вероятности (функция распределения вероятностей ). Можно доказать, что СВ , удовлетворяющая уравнению , имеет плотность вероятности . Таким образом, розыгрыш значения непрерывной СВ с заданной плотностью вероятности сводится к процедуре разыгрыша случайного числа . Значение находится из уравнения (рис. 4)

. (12)

Здесь обозначает обратную функцию по отношению к . Рассмотренный метод моделирования непрерывной СВ называется методом обратных функций.

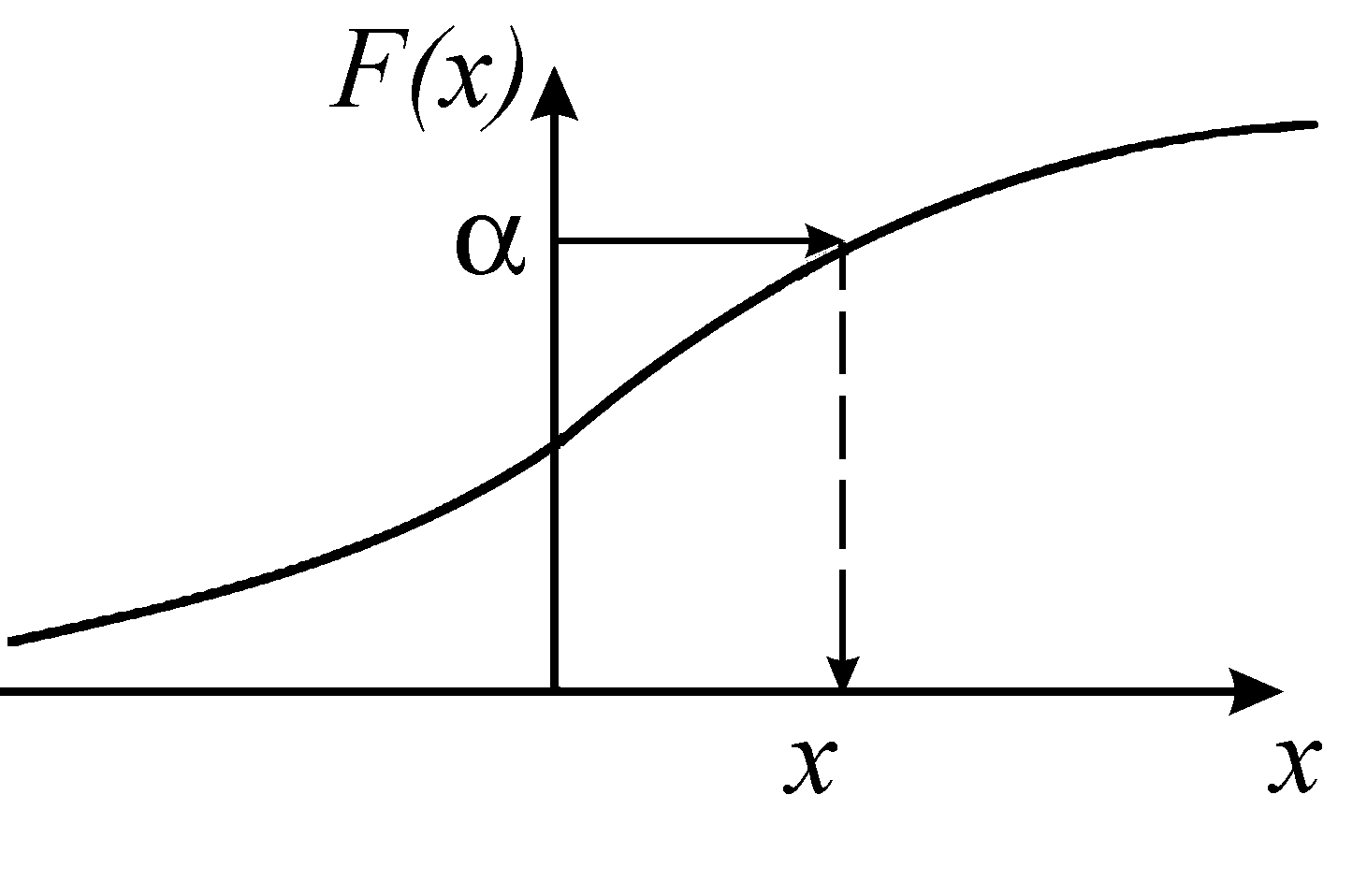
Рис. 4

Алгоритмы моделирования некоторых типов случайных величин Экспоненциальное распределение

Случайной величине с экспоненциальной плотностью вероятности

(13)

где – параметр распределения, соответствует функция распределения

.

На основании метода обратных функций найдем (см. рис. 4):

.

Решая относительно получим

.

Так как  СВ с равномерным распределением в интервале [0; 1], то также СВ с равномерным распределением в интервале [0; 1]. Окончательно получим

.

Пуассоновская случайная величина Распределение вероятностей числа событий на интервале времени для пуассоновской св с параметром определяется выражением

. (14)

Пуассоновский поток событий является простейшим потоком, для которого интервалы времени между соседними событиями являются независимыми СВ с экспоненциальной плотностью вероятности (13). Моделирование выполняется по следующей схеме: последовательно разыгрываем значения СВ с экспоненциальной плотностью вероятности до тех пор, пока не выйдем за пределы временного интервала (рис. 5). Число точек на интервале и есть значение пуассоновской случайной величины Для реализации, показанной на рис. 5, .

Рис. 5

Гауссовская случайная величина

Гауссовская (нормальная) СВ имеет плотность вероятности

. (15)

Здесь – среднее значение, – дисперсия СВ . Используя метод обратных функций, можно показать, что значение СВ вычисляется по формуле

,

где – обратная функция по отношению к функции Лапласа , определенной выражением (7).

Однако этот алгоритм на практике не применяют из-за больших затрат машинного времени. Это связано с тем, что при использовании ММК необходимо получать достаточно много значений СВ для вычисления результата с приемлемой точностью. Поэтому распространен другой алгоритм, позволяющий получать сразу два независимых значения гауссовской СВ и с нулевыми средними и :

где − координаты изотропного вектора на плоскости. Это означает, что точка имеет равномерное распределение на окружности с единичным радиусом. Моделирование :

1)

2) если , то повторяем 1) и т. д., иначе

3) .

Заданные значения и можно учесть с помощью линейного преобразования

. (16)

Другой способ моделирования гауссовской СВ основан на центральной предельной теореме, согласно которой сумма большого числа независимых СВ имеет приближенно гауссовское распределение. Чем больше слагаемых, тем точнее аппроксимация распределения суммы гауссовской плотностью вероятности. Например, сумма

уже при значении с хорошей степенью точности может считаться гауссовской СВ, пригодной для решения многих прикладных задач. Так как и , то СВ необходимо пронормировать

. (17)

В результате получим СВ с нулевым средним и единичной дисперсией. Далее необходимо выполнить линейное преобразование (16) для перехода к СВ с заданными значениями среднего и дисперсии.