Лабораторное задание

1. Для датчиков псевдослучайных чисел в приложениях MathCad, Excel и на языке Pascal вычислить оценки среднего, дисперсии и построить гистограммы относительных частот. Сравнить полученные оценки с точными значениями математического ожидания и дисперсии .

2. Разработать алгоритм вычисления площади (объема) заданной фигуры методом Монте-Карло и написать для него программу на ЭВМ. Определить величину относительной средне-квадратичной ошибки вычисленной оценки для различных прямоугольных областей , содержащих заданную фигуру (см. рис. 2). Найти точное значение площади (объема) заданной фигуры и сравнить полученные результаты.

3. Оформить в электронном виде отчет по результатам лабораторной работы, включив в него: цель работы, результаты исследование датчиков случайных чисел, алгоритм вычисления площади (объема) заданной фигуры и результаты расчетов. Отчет должен содержать обсуждение полученных результатов.

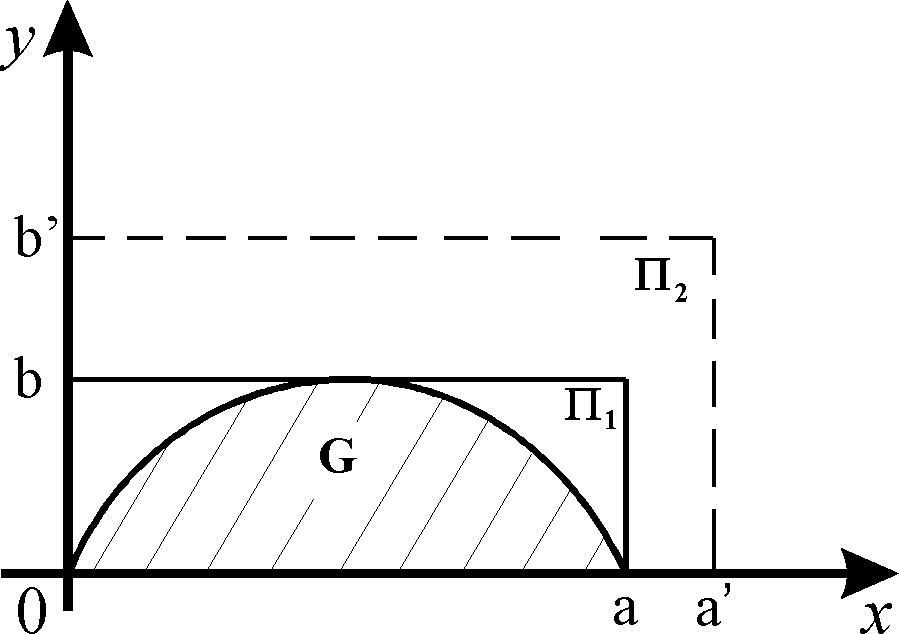
Рис. 2

Указания. Для вычисления объема (площади ) заданной геометрической фигуры необходимо разыграть координаты случайных точек с равномерным распределением в прямоугольной области (см. рис. 1, 2). Тогда оценки величины объема (площади ) можно вычислить по формулам:

,

,

где – число точек, попавших в область . Значение СВ с равномерной плотностью вероятности в заданном интервале можно получить с помощью линейного преобразования

. (10)

Здесь и далее обозначает СВ с равномерной плотностью вероятности в интервале [0; 1] (1). Более подробно моделирование случайных чисел с заданным законом распределения будет рассмотрено в материалах к лабораторной работе 2. Величину относительной среднеквадратической погрешности оценок объема (площади ) можно вычислить по формуле:

.

Контрольные вопросы

1. Чем отличаются последовательности случайных и псевдослучайных чисел?

2. Какими преимуществами обладают датчики псевдослучайных чисел и почему их удобно использовать для отладки программ?

3. Каким требованиям должны удовлетворять датчики псевдослучайных чисел?

4. Что можно сказать о точности результатов, полученных методом численного моделирования, и как они зависят от объема выборки?

5. Определите величину интервала в котором находится найденная оценка площади (объема) заданной фигуры с вероятностью 0,9. Значения функции Лапласа приведены в приложении 3.

ЛАБОРАТОРНАЯ РАБОТА 2

Моделирование случайных величин с заданным законом распределения

Цель работы: научиться моделировать случайные величины с заданным законом распределения

Общие сведения

Моделирование дискретных случайных величин

Рассмотрим дискретную СВ с рядом распределения

, (11)

где . Для того чтобы моделировать эту величину, разделим интервал [0; 1] на интервалы (рис. 3) такие, что длина равна вероятности . Можно доказать следующую теорему.

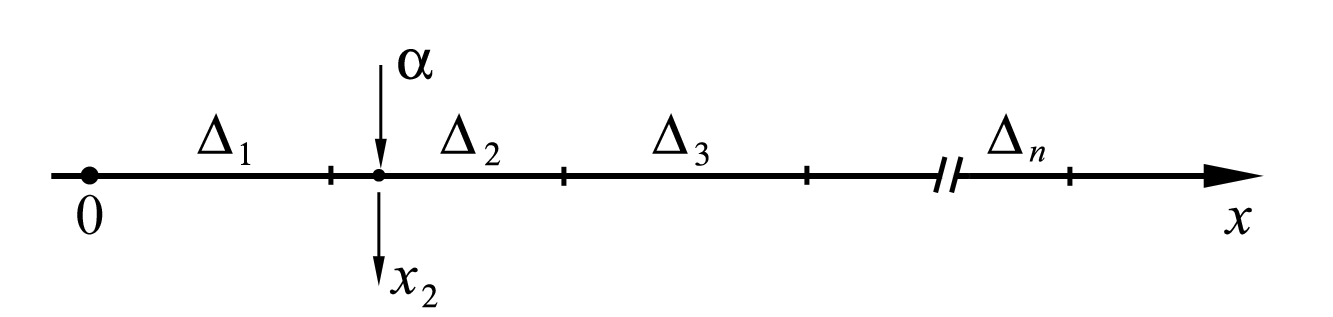
Рис. 3

Теорема. Случайная величина , определенная выраже-нием если , имеет ряд распределения вероятностей (11). Схема моделирования: разыгрываем случайное число и определяем интервала , в который оно попало. В результате получим соответствующее значение СВ (для показанной на рис. 3 реализации ).