Лабораторная работа 1 Метод численного моделирования (Метод Монте-Карло)

Цель работы: ознакомиться со встроенными датчиками псевдослучайных чисел в приложениях MathCad, Excel и на языке Pascal; научиться вычислять площадь заданной фигуры или объем тела методом Монте-Карло.

Общие сведения

В последнее время область приложений метода численного моделирования или метода Монте-Карло существенно расширилась в связи с бурным развитием вычислительной техники. Особо следует отметить значительный прогресс, связанный с увеличением быстродействия вычислительных машин, что особенно важно при использовании метода Монте-Карло.

Определение. Методом Монте-Карло (ММК) называется численный метод решения математических задач при помощи моделирования случайных величин.

Необходимо отметить, что ММК используется для решения любых математических задач, а не только задач вероятностного происхождения. Название «Монте-Карло» произошло от города Монте-Карло, известного своими казино, т. к. простейшим прибором для генерирования случайных чисел служит игральная рулетка. Возникновение метода Монте-Карло связывают с именами Дж. Неймана, С. Улама, Н. Метрополиса, Г. Канна и Э. Ферми, которые в 40-х годах работали в Лос-Аламосе. Официальной датой рождения ММК считают 1949 год, когда появилась статья под заглавием «Метод Монте-Карло» (Metropolis N., Ulam S.M. The Monte Carlo method. J. Amer. Statist. Assoc.,1949, 44, №247. P. 335−341).

Построение алгоритмов ММК основано на сведении задач к расчету математических ожиданий. Это означает, что для вычисления скалярной величины нужно придумать такую случайную величину , для которой ее математическое ожидание . Тогда, получив в численном эксперименте независимых значений можно найти, что

.

Пример. Требуется оценить объем некоторой ограниченной пространственной фигуры , показанной на рис. 1.

В

Рис. 1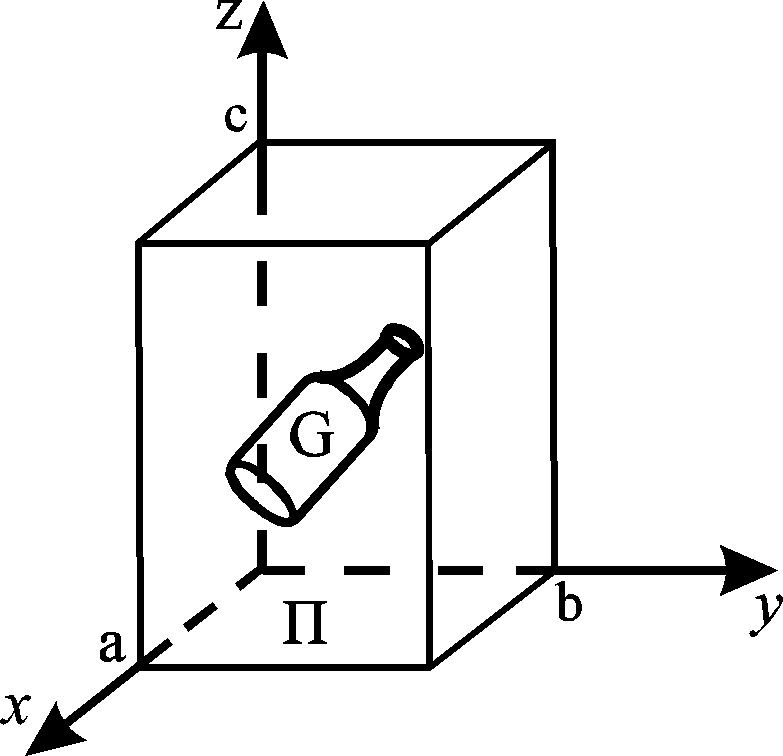

озьмем прямоугольный параллелепипед , содержащий область . Объем параллелепипеда П известен и равен . Разыграем координаты случайных точек, равномерно распределенных в области , и обозначим через количество точек, попавших в область G. При большом будет приближенно выполняться соотношение

,

из которого найдем

.

В нашем примере случайная величина

а среднее арифметическое равно

.

При решении задач ММК следует:

1. Удобно выбрать случайную величину (СВ) для решения конкретной задачи;

2. Научиться находить значения произвольной СВ . Решение второй проблемы связано с получением значений некоторой стандартной СВ, имеющей равномерное распределение в интервале [0; 1].

Моделирование случайных величин с равномерным распределением в интервале [0; 1]

Плотность вероятности СВ , равномерно распределенной в интервале [0; 1], равна

(1)

Функция распределения вероятностей имеет вид

Математическое ожидание , а дисперсия Иногда в качестве стандартной используют дискретную СВ , ряд распределения вероятности Р которой имеет вид

	0	1	2 … 9
Р	0,1	0,1	0,1 …. 0,1

Будем называть  случайным числом, а  случайной цифрой. Установим связь между и Представим число в виде бесконечной десятичной дроби

. (2)

Можно доказать следующую теорему: десятичные цифры случайного числа представляют собой независимые случайные цифры. Наоборот, если независимые случайные цифры, то формула (2) определяет случайное число.

Замечание. В вычислениях всегда используют числа с конечным числом десятичных знаков, поэтому случайные числа заменяют на случайные конечные дроби .

Таблица случайных чисел. Предположим, что осуществлено независимых опытов, в результате которых получено случайных цифр . Записав эти цифры в порядке появления, получим таблицу случайных цифр. При проведении расчетов можно использовать как сами цифры, так и конструировать из них случайные числа .

Существуют физические датчики случайных чисел. Для их построения используют шумящие радиоэлектронные приборы. Они применяются довольно редко, т. к. являются неудобными для практического использования и требуют постоянного контроля качества случайных чисел. Кроме этого нет возможности повторно воспроизвести выборочную последовательность необходимую на стадии отладки программ и повторения расчетов.