Лабораторное задание

1. Реализовать на ЭВМ алгоритм метода Монте-Карло моделирования СМО, позволяющий вычислять: относительную и абсолютную пропускную способность СМО, среднюю интенсивность потока заявок, покинувших СМО необслуженными, среднее время ожидания в очереди, средний интервал времени между событиями выходного потока. Входной поток заявок – поток Эрланга порядка с параметром (20). Время обслуживания имеет экспоненциальную плотность вероятности (13) с параметром . Число мест в очереди , число обслуживающих устройств и порядок потока Эрланга приведены в таблице, значения параметров и выбрать самостоятельно.

2. Вычислить оценки указанных в задании характеристик СМО и определить величину их относительной среднеквадратической погрешности.

3. Построить гистограмму величины интервала времени между событиями выходного потока.

4. Провести исследование полученных результатов на устойчивость к принятой модели, изменив вид функции плотности вероятности интервалов времени между соседними заявками входного потока. При этом параметры новой подобрать так, чтобы величина среднего интервала 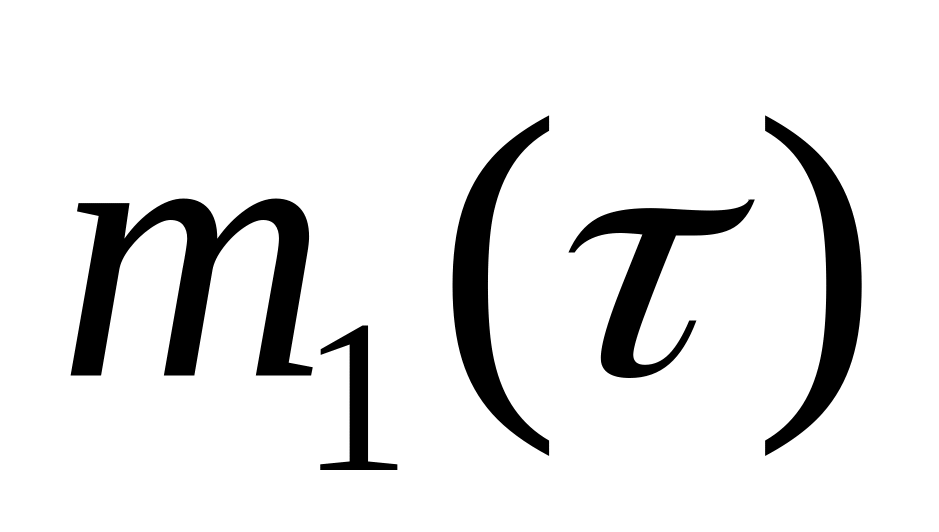осталась неизменной.

5. По результатам лабораторной работы оформить отчет, который должен содержать: цель работы, характеристики заданной СМО, ее статистическую модель, описание алгоритма численного моделирования, результаты расчетов, их обсуждение и основные выводы.

Варианты заданий для лабораторных работ 3, 4

Номер варианта
1	2	2	2
2	3	2	2
3	4	2	2
4	2	3	2
5	3	3	3
6	4	3	3
7	2	4	3
8	3	4	3
9	4	4	3
10	2	2	4
11	3	2	4
12	4	2	4
13	2	3	5
14	3	3	5
15	4	3	5

Контрольные вопросы

1. Какой поток событий называется рекуррентным?

2. Какой поток событий называется простейшим?

3. Какой вид имеет граф состояний рассмотренной вами СМО?

4. Перечислите основные компоненты СМО.

5. Что такое очередь и дисциплина очереди?

6. Что такое абсолютный и относительный приоритет заявки?

7. Какие параметры характеризуют эффективность работы СМО?

8. Какова эффективность рассмотренной вами СМО?

9. Как можно повысить эффективность СМО?

10. Что характеризуют результаты расчетов при различных статистических характеристиках входного потока?

11. Что такое обозначения Кендалла для СМО?