Потоки событий
Основным понятием при рассмотрении случайных процессов, протекающих в системах с дискретными состояниями и непрерывным временем, к которым относятся СМО, является понятие потока событий.
Определение. Потоком событий называется последовательность однородных событий, следующих одно за другим в случайные моменты времени (поток автобусов на данной остановке, поток отказов какой-то системы и т. п.). Поток событий можно изображать последовательностью точек на оси времени, как это показано на рис. 6.
Рис. 6
Особое место занимают потоки событий, обладающие свойствами − стационарности, отсутствия последействия, ординарности:
Поток событий называется стационарным, если вероятность попадания событий в интервале времени
зависит от
и не зависит от
.
Это означает, что интенсивность потока
событий не зависит от времени. Такие
потоки событий часто встречаются на
практике. Однако об их стационарности
строго можно говорить только на
ограниченном интервале времени.
Распространение этого свойства на
весь временной интервал является
удобным приемом.Поток событий называется потоком без последействия, если события, образующие поток, появляются в последовательные моменты времени независимо друг от друга.
Поток событий называется ординарным, если вероятность осуществления на бесконечно малом интервале времени двух и более событий
пренебрежимо малы по сравнению с
вероятностью одного события
,
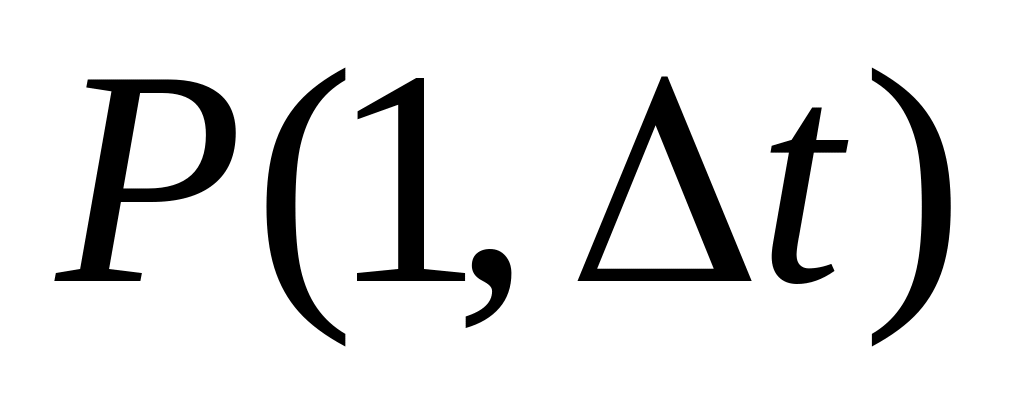т. е. выполняется условие
Определение. Поток событий называется простейшим, если он стационарен, ординарен и не имеет последействия. Для такого потока вероятность появления на интервале времени событий определяется формулой Пуассона (14).
Для простейшего
потока интервал
между соседними событиями имеет
экспоненциальное распределение (13).
Если рассматривать бесконечно малый
временной интервал
,
то с учетом ординарности пуассоновского
потока
.
Отсюда следует, что
.
Определение.
Поток событий называется рекуррентным
или потоком «Пальма», если он стационарен,
ординарен, а интервалы времени
между
соседними событиями представляют собой
независимые случайные величины с
одинаковым произвольным распределением.
Из определения следует, что простейший
поток – это частный случай рекуррентного.
Интервалы времени
имеют одинаковое экспоненциальное
распределение, а их независимость
обусловлена тем, что простейший поток
есть поток без последействия.
Важными для практики являются потоки Эрланга, которые образуются в результате «просеивания простейшего потока». Поток Эрланга n-го порядка получается, если в исходном простейшем потоке сохранить каждое n-е событие. На рис. 7 показан пример формирования потока Эрланга 4-го порядка.
Рис. 7
Простейший поток является потоком Эрланга первого порядка. Можно показать, что плотность вероятности интервала времени между соседними событиями в потоке Эрланга k-го порядка имеет вид:
, (20)
где
– средняя интенсивность порождающего
простейшего потока. При этом среднее
и дисперсия СВ
равны
,
.