Точні множини:

На практиці для їх відшукання зручно використовувати наступний критерій.

Теорема 2(критерій точних меж): Нехай М – не порожня числова множина, яка обмежена а) знизу чи в) зверху. Тоді:

1. 

2. 

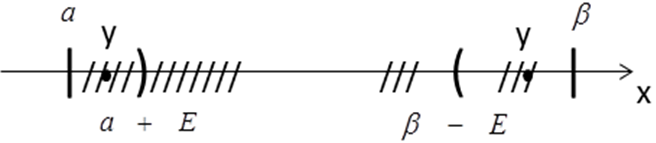
Метод математичної індукції. Нерівність Бернуллі. Біном Ньютона

Множина натуральних чисел N має важливу властивість. Яку називають принципом найменшого елемента.

Довільна не порожня підмножина має найменший елемент. У свою чергу це твердження рівносильне іншому твердженню, що називається принципом математичної індукції.

Нехай , тоді якщо:

1. і 2) з того, що 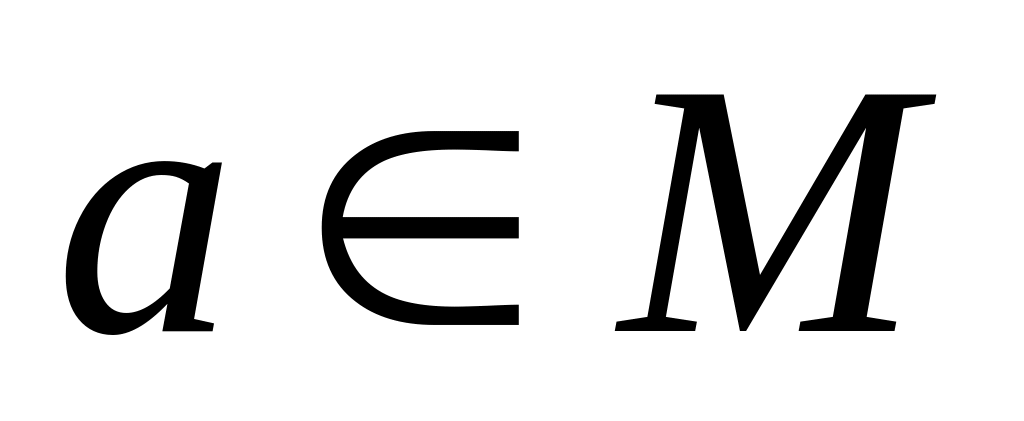, випливає, що , то .

Часто принцип математичної індукції (ПМІ) пов’язують з деяким твердженням Т_n, яке залежить від . Тоді його форму виражають у такій формі.

Формула 1: Нехай при визначити твердження Т_n. Тоді якщо:

1. Твердження Т_n правильне.

2. З правильності Т_n випливає правильність Т_n+1 , то твердження Т_n правильне .

Також множину узагальнюють за формулою 1 розглянувши замість множину цілих чисел , де .

Відповідно ПМІ залишиться у формі формули 2.

Формула 2: Нехай для , задане твердження Т_n.

Тоді якщо:

1. Правильність Т_n.

2. З правильності Т_n випливає правильність Т_n+1 , то Т_n правильна .

Нарешті більш зручно може виявити ще одна форма ПМІ.

Теорема 3: Нехай задане твердження Т_n , , тоді якщо:

1. Правильне твердження Т₁.

2. З припущення тверджень Т₁, Т₂ … Т_к випливає правильність Т_к+1, , то твердження Т_n правильне .

Отже «принцип найменшого числа» «ПМІ» F1 F2 F3.

Метод доведення твердження Т_n , який базується на ПМІ називають методом математичної індукції (ММІ).

Алгоритм ММІ:

1. Перевірити правильність Т₁.

2. Припустити, що правильне твердження Т_k.

3. Довести, що .

4. Зробити висновок, що Т_n правильне .

Властивість неперервності:

, якщо .

Доведення ММІ:

1. □ - нерівність правильна. ■

2. Припустимо, що при нерівність правильна .