Построение сетевого графика

Приведём алгоритм построения сетевого графика, идея которого изложена в [6].

График строится по списку непосредственно предшествующих работ, так что предварительно нужно составить этот список так, как указано выше. Общие формулировки пунктов алгоритма будут сопровождаться построением сетевого графика для проекта из примера 1. В целом построение разбивается на два этапа: на 1-ом этапе строится сетевой график с большим количеством фиктивных дуг, на 2-м этапе число фиктивных дуг по возможности сокращается, полученный сетевой график упорядочивается.

Этап 1.

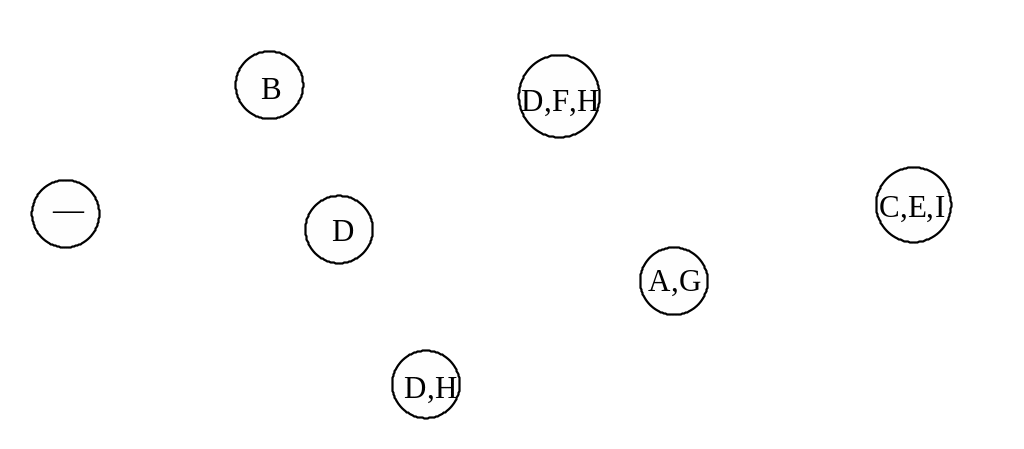
Шаг 1. Множества непосредственно предшествующих работ обозначим в виде вершин. Число таких вершин – число различных групп работ в правой части таблицы 3.

В примере 1:

, , , , ,

– конец проекта

Шаг 2. Введём ещё вершину для конца проекта, обозначив её набором работ, не встречающихся в правой колонке таблицы 3.

Шаг 3. Расположим эти вершины, называемые для краткости "старыми вершинами", в произвольном порядке на плоскости (в компьютере – произвольно пронумеруем).

Рекомендуется события изображать в порядке предшествования, поэтому начало проекта, обозначенное {—} лучше расположить слева, конец проекта – справа, предшествующее –— левее от последующего (если это известно).

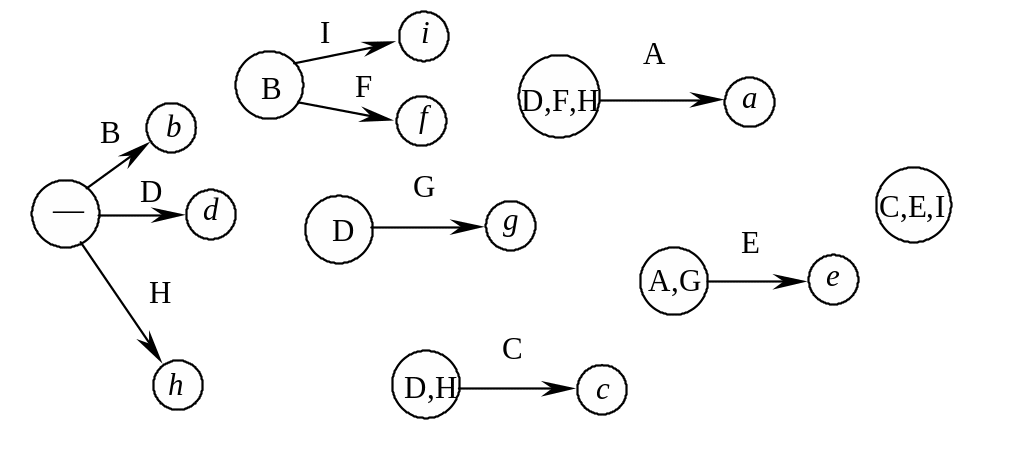
Шаг 4. Изобразим каждую работу проекта в виде дуги, выходящей из той старой вершины, которая является множеством непосредственно предшествующих работ для данной работы. Конец изображаемой дуги обозначим как новую вершину. Название новой вершины удобно дать в соответствии с названием изображаемой работы, например, прописной буквой t, если работа называлась T.

Шаг 5. Свяжем полученные части с помощью фиктивных дуг. Начала фиктивных дуг находятся в новых вершинах – концах работ, а концы фиктивных дуг находятся в старых вершинах, а именно в тех, которые содержат эти работы в своём обозначении. Например, H содержится в обозначениях вершин и , поэтому рисуются две фиктивные дуги из конца работы H, т.е. из . Первая начинается в и заканчивается в , другая начинается в и заканчивается в .

Шаг 6. Сделаем правильную нумерацию вершин полученной сети.

Рис. 4.

Этап 2.

При сокращении фиктивных дуг используются следующие правила.

Правило 1. Если фиктивная дуга ( i, j ) соединяет вершину i с вершиной j, а из i в j уже есть другой путь (из действительных или фиктивных дуг – неважно), то фиктивную дугу следует удалить, стереть. Вершины i, j при этом не изменяются. 

Это правило приоритетное, т.е. оно применяется, если возможно, прежде других правил.

Правило 2. Пусть ( i, j ) – фиктивная дуга, которая единственная среди дуг сети начинается в i (единственная выходящая из i) или же единственная среди дуг сети, заканчивается в j. Тогда эту фиктивную дугу можно сократить, объединив вершины i, j в одну (говорят, сжав фиктивную дугу), если при этом не образуются параллельные дуги. Для новой объединённой вершины обычно оставляют обозначение i или j. 

Правило 3. Фиктивную дугу ( i, j ) можно сжать, объединив её начало i и конец j в одну вершину, если при этом не образуются лишние связи предшествования, т.е. связи, которых нет в проекте, и не образуются параллельные дуги. 

Правило 2 выделено из правила 3, так как образование параллельных дуг легче проверяется, чем образование лишних связей, а при условиях, в которых правило 2 действует, лишние связи не могут возникнуть.

Шаг 7. Применим правила 1–3 для последовательного сокращения фиктивных дуг, пока в сетевом графике не останутся действительные работы и те фиктивные дуги, без которых нельзя обойтись (см. примеры 3, 4).

На рис.4 нет фиктивных дуг для сокращения по правилу 1. Сократим одну дугу, например, (4, 16) по правилу 2. К ней это правило применимо, так как из вершины 4 других выходящих нет, а сокращение (сжатие) дуги (4, 16) не приводит к появлению параллельных дуг – в данном случае двух дуг (3, 16). Для объединённой вершины сохраним обозначение 16. Получим график на рис.5.

Рис. 5. График после сокращения (4, 16)

Так как дуги, которую можно сократить по правилу 1, снова нет, сокращаем следующую по правилу 2 и так далее.

После сокращения (2, 3), (6, 7), (5, 12), (8, 14), (13, 14), (15, 16), (11, 16) по правилу 2 получим сеть

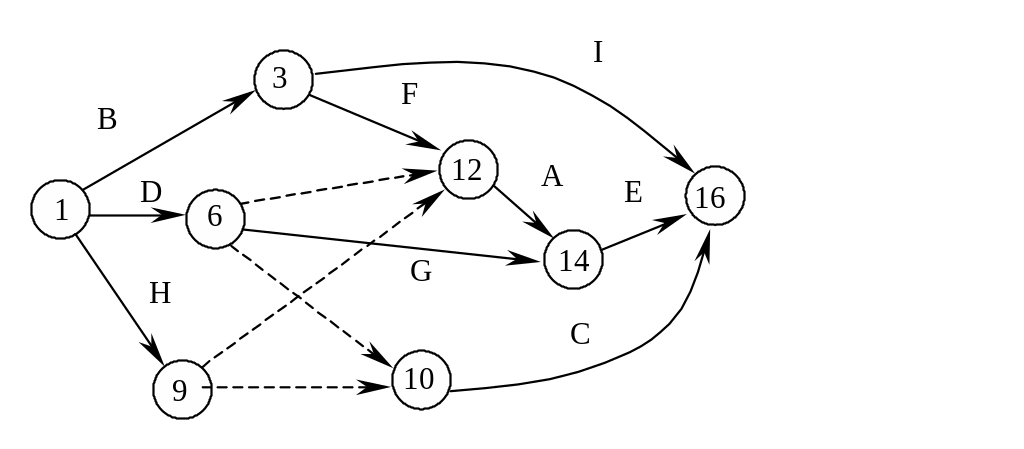
Рис. 6.

Оставшиеся фиктивные дуги можно попытаться сократить по правилу 3.

Дуги (6, 12) и (9, 12) сократить нельзя, так как работа C приобретает тогда зависимость от работы F (через фиктивные дуги (6, 10) или (9, 10)), которой нет в исходном проекте. Фиктивную дугу (6, 10) так же нельзя сократить, так как иначе работа G получает зависимость от H, чего нет в исходном проекте (на рис.6).

Фиктивную дугу (9, 10) можно сократить, так как при этом не возникает ни параллельных дуг, ни лишних связей предшествования. После сокращения (9, 10) получим сеть

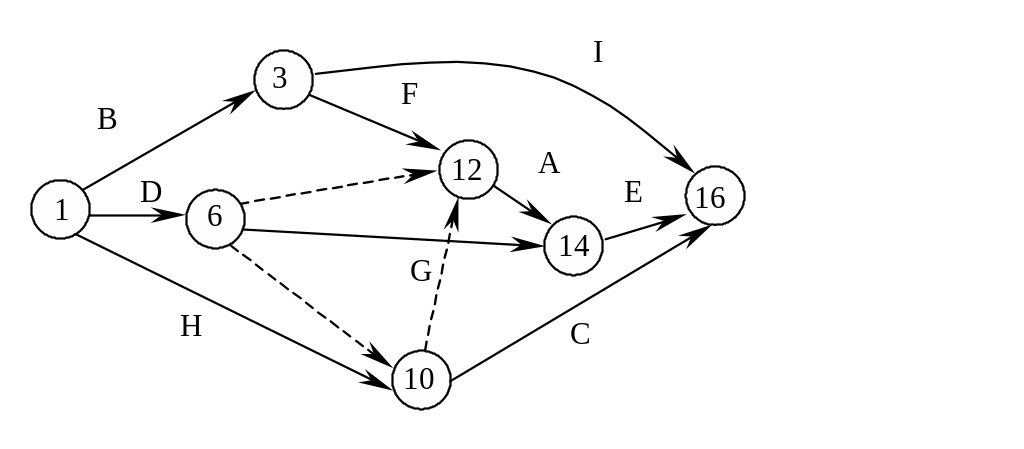
Рис. 7.

Рис. 8.

Теперь по правилу 1 нужно удалить (6, 12), так как из 6 в 12 есть другой путь: (6, 10, 12). Получим сеть

Дугу (10, 12) нельзя сократить, так как иначе появится несуществующая зависимость C от F.

Дугу (6,10) нельзя сократить, так как иначе появится лишняя связь G от H, а также образуются параллельные работы D, H (достаточно лишь одного из этих двух нарушений).

Шаг 8. Сделаем правильную нумерацию в полученной сети. Искомый сетевой график построен.

Рис. 9. Окончательный сетевой график.

Для хранения полученного графика, т.е. логической структуры проекта достаточно запомнить набор записей вида: {(1,2), B}, {(1,3), D}, {(1,4), H}, {(2,5), F}, {(2,7), I}, {(3,4), фикт.}, {(3,6), G}, {(4,5), фикт.}, {(4,7), C}, {(5,6), A}, {(6,7), E}.

С формальной точки зрения этот набор и есть сетевой график.