Сетевой график проекта

Математическим, формальным представлением объектов, между которыми попарно установлены некоторые связи, является граф. Сети являются частным случаем графов. Ограничимся случаем, необходимым в сетевом планировании.

Объекты называются вершинами и графически изображаются кружками. Связи считаются установленными между некоторыми парами из различных вершин и считаются односторонними. Графически связь изображается линией со стрелкой, или дугой, соединяющей две вершины. Согласно направлению связи, т.е. направлению стрелки, соединяемые вершины являются началом и концом дуги, или, другими словами, начальной и конечной вершинами дуги.

Будем считать, что между двумя вершинами есть не более одной дуги (нет "параллельных" дуг). Формально этого можно добиться, разбив дугу на две с помощью промежуточной вершины. В дальнейшем дугу будем записать в виде упорядоченной пары (a, b), где a – начало дуги, b – конец дуги.

Путём из вершины в вершину , или путём, начинающимся в и заканчивающимся в , называется последовательность вершин , где пары , , …, являются дугами. Графически путь представляет непрерывную направленную линию из дуг, согласованную с направлениями стрелок ("движения по стрелкам"). Если , т.е. если начало пути совпадает с концом пути, то путь называется контуром. Цепочкой из вершины в вершину называется последовательность из различных вершин, в которой дугами являются или , или , и т.д. Таким образом, цепочка соответствует линии из в без учёта направления стрелок. Замкнутая цепочка называется циклом.

Рис. 1

( a, c, b, d, f ) – путь ( b, d, f, c, b ) – контур ( a, b, c, f ) – цепочка ( a, b, c, a ) – цикл

Будем предполагать, что любые две вершины можно соединить цепочкой (соответствующий граф называется связным).

Определение. Конечная совокупность вершин и дуг (и их графическое изображение) называется сетью, если выполняются условия:

а) связности;

б) отсутствия петель (начало и конец дуги различны);

в) отсутствие параллельных дуг. 

Определение. Сеть называется бесконтурной, или упорядоченной сетью, если в ней нет контуров. 

Замечание. В литературе встречается также термин ациклическая сеть.

Сеть на рис.1 не является бесконтурной, т.к. есть контур ( b, d, f, c, b).

Н у м е р а ц и я вершин сети – это сопоставление вершинам номеров – натуральных чисел, при этом различным вершинам сопоставляются различные номера.

Определение. Нумерация называется правильной, если

а) номера идут подряд: 1, 2, …, m, где m – число вершин;

б) номер начала дуги меньше номера конца дуги, т.е. все дуги записываются в виде , где . 

В сетях, имеющих контур, правильной нумерации не может быть, так как для вершины контура с номером n получаем противоречивое неравенство .

В бесконтурных сетях правильная нумерация возможна и может быть проставлена по следующей процедуре (алгоритм Форда).

1. Найдём вершину, которая не является началом никакой дуги, т.е. из которой дуги не выходят. Такая вершина легко может быть найдена, если, начиная с любой вершины, двигаться по стрелкам дуг, переходя из вершины в вершину.

2. Присвоим найденной вершине текущий номер. Первый раз таким номером является m – число вершин сети.

3. Уменьшим текущий номер на одну единицу. Вычеркнем или пометим как-либо дуги, заканчивающиеся в вершине, только что пронумерованной. В дальнейшем считаем, что этих дуг нет в сети. Возвращаемся к шагу 1, т.е. все повторяем с начала.

Замечание. 1. Если не удаётся найти вершину в шаге 1, то в сети есть контур и правильная нумерация невозможна, так что алгоритм Форда является проверкой, будет ли сеть бесконтурной.

2. Правильных нумераций в сети может быть несколько.

Пример 2.

Неправильная нумерация

Правильная нумерация (1 и 2, 4 и 5 можно поменять местами)

Рис. 2.

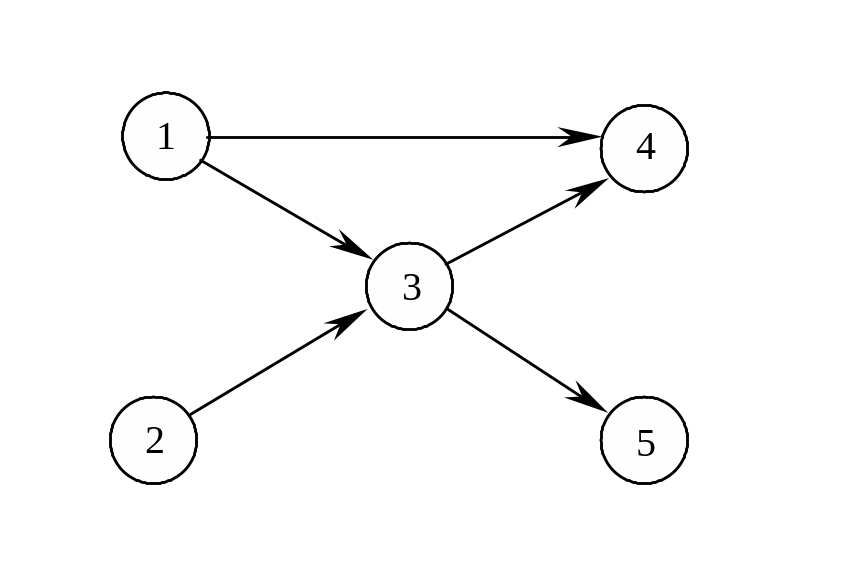
Дуги и вершины бесконтурной сети связаны отношением предшествования, аналогичным предшествованию работ и событий.

Определение. Вершина i предшествует вершине j, если из i в j существует хотя бы один путь, т.е. есть путь, в котором i встречается раньше, чем j .

Дуга предшествует дуге , если существует хотя бы один путь вида , т.е. путь, первой дугой которого является , и последней — . 

Отношение предшествования дуг и вершин бесконтурной сети также обладает свойствами (*) и (**) (транзитивностью и антирефлексивностью).

Сетевой график. Аналогия между работами, событиями с одной стороны и дугами, вершинами с другой стороны указывает на возможность представления проекта в виде бесконтурной сети. Такое представление называется с е т е в ы м графиком. Есть два вида сетевых графиков:

1-й вид: Работам проекта соответствуют дуги, а событиям – вершины.

2-й вид: Работам проекта соответствуют вершины, события при этом не имеют чётко выраженного представления.

Сетевые графики второго вида плохо приспособлены для решения расчётных и оптимизационных задач, особенно на компьютере, неестественны, так как длящийся процесс (работа) отображается вершиной, не имеющей протяжённости. По существу единственным их преимуществом является простота построения, что видно на рис.3, изображающем проект из примера 1. Здесь НП, КП – начало и конец проекта, остальные вершины – работы.

Рис. 3. Сетевой график 2-го вида, построенный по таблице 3.

В дальнейшем сетевые графики 2-го вида рассматриваться не будут, а сетевые графики первого вида будут называться просто сетевыми графиками, как это общепринято.

Итак, работы проекта соответствуют дугам, а события – вершинам сетевого графика. Дадим окончательное определение.

Определение. Сетевым графиком проекта называется безконтурная сеть со следующими свойствами:

1) Есть только одна вершина, не имеющая заканчивающихся в ней дуг. Она соответствует началу проекта (и так же называется).

2) Есть только одна вершина, не имеющая начинающихся в ней дуг. Она соответствует концу проекта (и так же называется).

3) Работы, события проекта, предшествуют друг другу тогда и только тогда, когда соответствующие им дуги, вершины предшествуют друг другу. 

В сетевом графике дуг может, а иногда и должно быть больше, чем работ в проекте. Эти "лишние" дуги называются фиктивными дугами или фиктивными работами и вводятся для указания того, что вершина – начало фиктивной дуги должна предшествовать вершине – концу фиктивной дуги. В сетевом графике они обычно обозначаются пунктиром.

Пример 3. Проект состоит из двух независимых работ A, B.

или

Событий, очевидно, также два: {—} – начало проекта и {A, B} – конец проекта. Сетевой график должен был бы выглядеть так:

Однако дуги A, B в этом случае являются п а р а л л е л ь н ы м и , имеют одинаковое обозначение в парах вершин: (1, 2), что не согласуется с определением сети. Поэтому правильный сетевой график должен выглядеть так:

или

(2, 3) – фиктивная дуга

Пример 4. Пусть четыре работы A, B, C, D некоторого проекта имеют следующие зависимости: C имеет непосредственно предшествующими A и B, D имеет одну непосредственно предшествующую B. Соответствующая часть сетевого графика должна быть такой:

( i, j ) – фиктивная дуга

Ясно, что ( i, j ) не может быть стёрта (удалена без объединения вершин), так как потеряется зависимость C от B, и не может быть сжата (с объединением вершин i, j в одну вершину), так как тогда работа D станет зависеть от работы A, что тоже неверно.