1.4. Характеристики роста экономики для мультипликативной производственной функции.

Пусть – значения выпуска, фондов, труда по различным годам, причем выпуски задаются одной и той же мультипликативной производственной функцией

. (5)

Отношения представляют собой темпы роста выпуска, фондов, труда. Из (5) при находим

. (6)

Пусть . (7)

После возведения равенства (6) в степень получаем

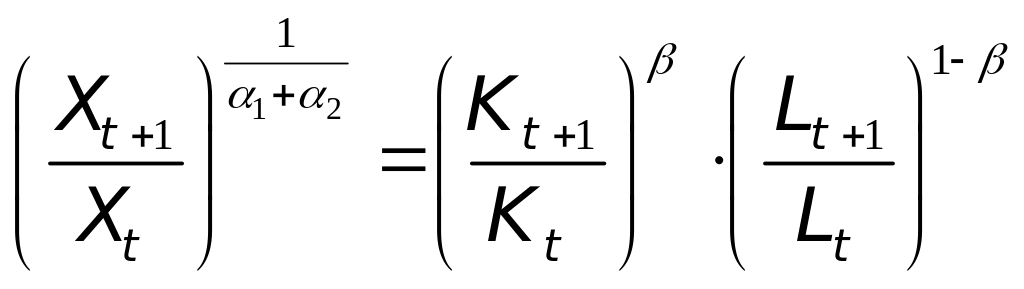. (8)

В равенстве (8) справа стоит обобщенное среднее геометрическое темпов роста факторов (при было бы просто среднее геометрическое) – единая характеристика темпов роста фондов и труда, подходящая для мультипликативных производственных функций. Если , то . Получаем, что в этом случае темп роста выпуска опережает средний темп роста факторов и экономика является растущей. Соответственно, при экономика является замедляющейся (если не сказать деградирующей). При экономику называют интенсивной, в противном случае – экстенсивной.

Рассмотрим темпы роста выпуска, фондов, труда по отношению к некоторому базовому периоду : . Это позволяет получить безразмерные величины, а также избавиться от параметра нейтрального коэффициента :

. (9)

С помощью обозначений (7) из равенства (8) можно получить представление

, (10)

где – масштаб экономики,

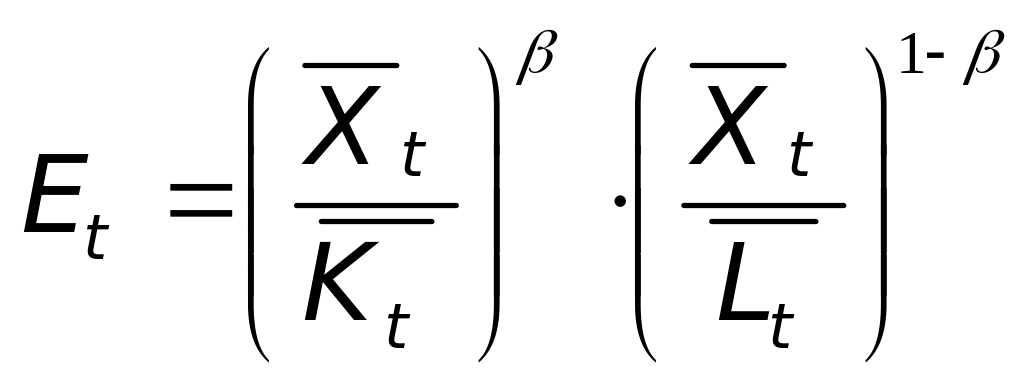– средняя эффективность экономики (обобщенное среднее геометрическое от эффективности по фондам (фондоотдачи) и от эффективности по труду (производительности труда) .

Тема 2. Модель Леонтьева.

Так кратко будем называть модель межотраслевого баланса В.В.Леонтьева. Другое название – модель «затраты - выпуск». Впервые рассматривалась советскими экономистами в 1920-х, однако всесторонне изучена и развита американским экономистом русского происхождения Василием Васильевичем Леонтьевым в 1930-40-х гг. (лауреатом Нобелевской премии по экономике 1973 г.). Ниже изложена математическая суть модели.

2.1. Определение модели и ее продуктивность.

Пусть экономика страны (точнее, ее производство) разбита на отраслей (в реальных моделях может быть до нескольких сотен). Каждая отрасль вырабатывает лишь один продукт, и каждый продукт производится лишь одной отраслью. При этом для производства продукта некоторой отрасли используются продукты других отраслей.

Рассмотрим выпуск продуктом за некоторый промежуток времени (обычно за год). Пусть через обозначено количество продукта -й отрасли, необходимое для выпуска одной единицы продукта - й отрасли, удельный расход, коэффициент прямых затрат. Важно не перепутать порядок индексов! Числа , очевидно, неотрицательны: , и при образуют квадратную матрицу размера .

Определение. Матрица называется технологической матрицей, или матрицей прямых затрат.

Неотрицательность означает неотрицательность матрицы :

0,

где в неравенстве справа написана нулевая матрица размера .

Пусть теперь – объемы выпуска (производства) продуктов соответственно 1-й, 2-й,…, -й отраслей , а – объемы продуктов, оставшихся от , после того, как их использовали в производствах всех отраслей. Кратко будем называть выпуском (грязным выпуском), а – потреблением (чистым выпуском) - й отрасли.

Выпишем эти соотношения между и (балансовые равенства).

Всего первого продукта производится . Из этого количества на производство второго продукта в объеме уходит , на производство третьего продукта в объеме уходит и т.д. Кроме того, на производство первого же продукта в объеме уходит (например, при производстве досок сами же доски используются). Тогда остаток после производства равен

.

Аналогично для второго продукта

,

и так далее. Получаем систему равенств

… (1)

Собственно говоря, равенства (1) и есть модель Леонтьева.

В дальнейшем проще будет пользоваться матричной записью. Обозначим через

и через векторы–столбцы выпусков и потребления.

Они также должны быть неотрицательными:

0, (2)

0. (3)

Кратко в матрично-векторной записи модель Леонтьева можно записать как равенство

, (4)

или

,

где – единичная матрица размера (на диагонали единицы, остальные – нули).

Если считать вектор потребления известным, а вектор выпуска неизвестным, система (4) является квадратной (число уравнений равно числу неизвестных, и равно ) системой линейных алгебраических уравнений.

Пользуясь понятием «обратная матрица» (матрица, которая после умножения на исходную как справа, так и слева, дает единичную ) решение системы (4) записывается как

, (5)

где – обратная к матрица, называемая матрицей полных затрат.

С экономической точки зрения модель Леонтьева естественна, когда для любого вектора потребления можно вычислить некоторый вектор выпуска так, чтобы балансовые равенства выполнялись. Это приводит к понятию продуктивность.

Определение. Модель Леонтьева называется продуктивной, если для любого вектора (набора) потребления найдется некоторый вектор выпуска , удовлетворяющий (4) .

Пример 1. Пусть = 2 (есть всего две отрасли).

		1	2
А =	1	0.5	0
	2	10	0,1

Для производства 1 единицы первого продукта необходимо 0.5 единиц этого же первого продукта и 10единиц второго продукта. Для производства 1 единицы второго продукта необходимо 0.1 единиц этого же второго продукта (а первый продукт не нужен).

Пусть необходимо получить для потребления 2 единицы первого продукта ( ) и 5 единиц второго продукта ( ).

Система (1) имеет вид

, или

. Решением системы являются значения .

Если вместо 2 и 5 взять произвольный вектор потребления , то получим решение

Продуктивность модели очевидна. Заметим, что если взять произвольный неотрицательный выпуск 0, то неотрицательное потребление может и не получиться. Например, если взять в этом примере , то получим .

Пример 2. «Слегка» исправим пример 1. Пусть

		1	2
А =	1	0	0,5
	2	10	0,1

Для производства 1 единицы первого продукта необходимо 10единиц второго продукта. Для производства 1 единицы второго продукта необходимо 0.1 единиц этого же второго продукта и 0.5 единиц первого продукта.

Пусть необходимо получить для потребления 2 единицы первого продукта ( ) и 5 единиц второго продукта ( ).

Система (1) имеет вид

, или

. Решением системы являются значения . Модель непродуктивна.

Математически легко доказывается, что

Утверждение 1. Если модель продуктивна, то система (4) имеет решение при любом векторе , и это решение единственно. Здесь для , не обязаны быть неотрицательными, то есть (2 – 3) может не выполняться.

Другими словами, матрица существует (известно, что многие матрицы не имеют обратной).

Утверждение 2. Модель Леонтьева продуктивна тогда и только тогда когда матрица полных затрат неотрицательна:

0. (6)

Чтобы это выяснить, нужно найти. Это легко сделать в EXCEL. Там для этого есть функция (в категории «математические») МОБР. Естественно, предварительно нужно вычислить матрицу . Матрицу можно найти и в ручную, если знать преобразования Гаусса (см. раздел 3. Методические указания к контрольной работе)

В примере 1

		1	2
=	1		0
	2

.

Математически также (сложнее) доказывается, что

Утверждение 3. Модель Леонтьева продуктивна тогда и только тогда когда матрица полных затрат может быть представлена в виде ряда:

, (7)

что дает представление

. (8)

Равенство (8) имеет ясную экономическую интерпретацию. Чтобы получить в остатке , нужно как минимум произвести , а для этого необходимо произвести еще (прямые затраты для ). Чтобы произвести эти , необходимо произвести еще (прямые затраты для ) и так далее.

Равенство (7) объясняет, почему называется матрицей полных затрат.

Замечание. Для читателей, имеющих математическое образование, скажем, что равенство (7) справедливо тогда и только тогда когда спектральный радиус матрицы , то есть максимальный модуль собственных чисел, меньше 1.