
- •Математический факультет
- •Методические указания
- •Задания к контрольной работе
- •Сыктывкар 2006
- •Предмет сетевого планирования
- •Структурное планирование
- •Предшествование работ. События. Списки предшествования
- •Список предшествующих работ Таблица 1
- •Сети. Сетевой график проекта
- •Построение сетевого графика
- •Календарное планирование
- •Критическое время, критические работы, критический путь
- •Временные параметры событий
- •Временные параметры работ.
- •Диаграмма Гантта.
- •Контрольные задания
- •Вариант 3 Вариант 4
- •Вариант 5 Вариант 6
- •Вариант 7 Вариант 8
- •Вариант 9 Вариант 10
- •Вариант 13 Вариант 14
- •Вариант 15 Вариант 16
- •Вариант 17 Вариант 18
- •Вариант 19 Вариант 20
- •Вариант 21 Вариант 22
- •Вариант 23 Вариант 24
- •Вариант 25 Вариант 26
- •Вариант 27 Вариант 28
- •Вариант 29 Вариант 30
- •Рекомендуемый библиографический список
Временные параметры событий
Каждое событие i
проекта P (вершина i
на сетевом графике) имеет набор всех
предшествующих этому событию работ
и набор всех последующих за этим событием
работ. Если рассмотреть эти множества
работ как самостоятельные проекты, то
как бы получаются предшествующий проект
![]() и последующий проект
и последующий проект
![]() .
.
|
1 – начало проекта P. i – событие проекта Р. N – конец проекта Р. P' – предшествующие работы. P" – последующие работы |
Для
![]() событие i является
концом проекта,
а для
событие i является
концом проекта,
а для
![]() –
началом проекта.
Другие работы исходного проекта, не
входящие ни в
,
ни в
,
являются независимыми от события i
.
–
началом проекта.
Другие работы исходного проекта, не
входящие ни в
,
ни в
,
являются независимыми от события i
.
Проекты
и
имеют свои критические времена
![]() и
и
![]() ,
равные численно длинам максимальных
путей, соответственно из
,
равные численно длинам максимальных
путей, соответственно из
![]() в
в
![]() и из
в N - конец исходного
проекта. Но эти длины равны потенциалам
и из
в N - конец исходного
проекта. Но эти длины равны потенциалам
![]() ,
,
рассчитанным, соответственно, с начала
и конца проекта. Получаем, что
,
,
рассчитанным, соответственно, с начала
и конца проекта. Получаем, что
![]() ,
,
![]() .
.
Значение показывает согласно определению критического времени и проекта , какое наименьшее время требуется для выполнения , т.е. до наступления события i .
Значение показывает, какое наименьшее время требуется для выполнения проекта после наступления события i .
Определение.
Ранним сроком
![]() события i называется
наименьшее
время после начала проекта, через которое
событие i может
наступить.
события i называется
наименьшее
время после начала проекта, через которое
событие i может
наступить.
Этот параметр как раз равен наименьшему времени, необходимому для завершения предшествующих работ, т.е.
![]() ,
,
где
![]() –
потенциалы, рассчитанные с начала.
–
потенциалы, рассчитанные с начала.
В частности, всегда
![]() ,
,
![]()
![]() .
Ранние сроки не зависят от
.
Ранние сроки не зависят от
![]() ,
т.е. они являются "внутренними"
параметрами проекта.
,
т.е. они являются "внутренними"
параметрами проекта.
Определение.
Поздним сроком
![]() события i называется
наибольшее
время (после начала проекта), через
которое событие не
должно наступить (иначе сорвётся
проектное время).
события i называется
наибольшее
время (после начала проекта), через
которое событие не
должно наступить (иначе сорвётся
проектное время).
Проект необходимо завершить к моменту , а минимальное время для вычисления следующих за событием работ равно , поэтому
![]() ,
,
где – потенциалы, рассчитанные с конца.
В частности, всегда
![]() ,
,
![]()
![]() .
Очевидно (докажите это!), что
.
Очевидно (докажите это!), что
![]() .
Поздние сроки являются "внешними"
параметрами, т.к. зависят от
.
.
Поздние сроки являются "внешними"
параметрами, т.к. зависят от
.
Определение.
Резервом
![]() события i называется
разность его позднего и раннего сроков.
события i называется
разность его позднего и раннего сроков.
Для событий, лежащих на
критическом пути, резерв равен разности
![]() ,
для остальных событий – больше
этой разности.
,
для остальных событий – больше
этой разности.
Приведём все временные параметры событий в примере 1.
Параметры событий Таблица 5.
i |
|
|
|
1 2 3 4 5 6 7 |
0 13 12 12 14 17 22 |
3 19 15 15 20 22 25 |
3 6 3 3 6 5 3 |
Временные параметры работ.
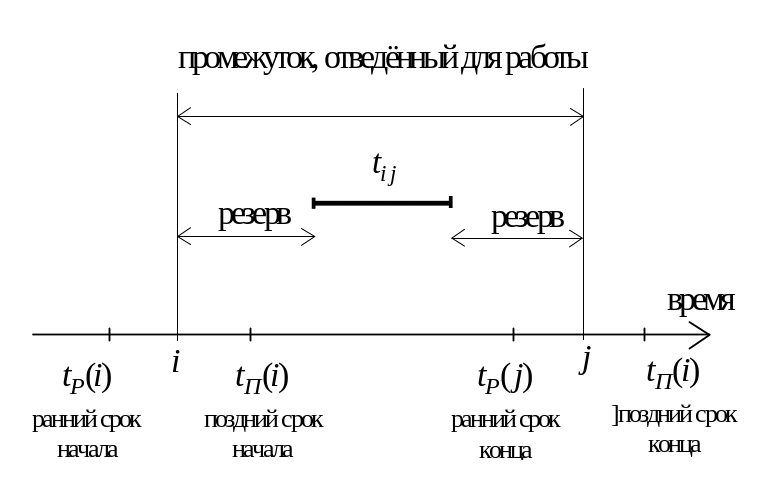
Определение. Ранним началом
![]() работы ( i, j
) называется наименьшее
время после начала проекта, через
которое работу можно
начать выполнять.
работы ( i, j
) называется наименьшее
время после начала проекта, через
которое работу можно
начать выполнять.
Очевидно, работу можно начать, как только закончатся предшествующие работы, т.е. когда наступит событие i – событие начала. Отсюда
![]() .
.
Определение.
Ранним окончанием
![]() работы ( i, j
) называется наименьшее время после
начала проекта, через которое работу
можно
закончить.
работы ( i, j
) называется наименьшее время после
начала проекта, через которое работу
можно
закончить.
Работу можно рано закончить, если её рано начать, поэтому
![]() ,
,
где
![]() –
время работы.
–
время работы.
В общем случае
![]() ,
но для некоторых
работ эти параметры совпадают.
,
но для некоторых
работ эти параметры совпадают.
Определение.
Поздним окончанием
![]() работы ( i, j
) называется наибольшее
время после начала проекта, позже
которого работу нельзя
закончить (иначе сорвётся
проектное время
работы ( i, j
) называется наибольшее
время после начала проекта, позже
которого работу нельзя
закончить (иначе сорвётся
проектное время
![]() ).
).
Событие j как раз означает окончание работ, заканчивающихся в j, в том числе работы ( i, j ), поэтому
![]() .
.
Определение.
Поздним началом
![]() работы ( i, j
) называется наибольшее
время после начала проекта, позже
которого работу нельзя
начать
(иначе сорвётся проектное время).
работы ( i, j
) называется наибольшее
время после начала проекта, позже
которого работу нельзя
начать
(иначе сорвётся проектное время).
Если работа поздно начинается, то она и поздно заканчивается, поэтому
![]() .
.
Позднее начало и окончание – "внешние" параметры, зависящие от .
Следующие определения резервов работ взяты из [1].
Определение. Полным резервом
![]() называется наибольшее время, на
которое можно увеличить время работы
(т.е. это прибавка по времени, запас),
если предшествующие
для ( i, j
) работы начинаются в ранние
сроки, а последующие
за ( i, j
) – в поздние
сроки.
называется наибольшее время, на
которое можно увеличить время работы
(т.е. это прибавка по времени, запас),
если предшествующие
для ( i, j
) работы начинаются в ранние
сроки, а последующие
за ( i, j
) – в поздние
сроки.
Другими словами, полный резерв это запас времени в самом "благоприятном" для работы случае, когда предшествующие рано заканчиваются и дают работе возможность для раннего начала, а последующие поздно начинаются и дают работе возможность для позднего окончания. Коротко: "до нас – рано, после нас – поздно".
Несложно получить, что (см. схему)
![]() ,
,
Полезны также формулы
![]() .
.
![]() .
.
Полный резерв – "внешний" параметр.
Критические работы полностью определяются через значения полных резервов. Работа ( i, j ) является критической тогда и только тогда, когда
![]() .
.
В случае, когда проектное время совпадает с критическим, т.е. когда проект вовсе не имеет резерва, резервы критических работ равны нулю, что и оправдывает название "критические".
Определение. Свободным резервом
![]() работы ( i, j
) называется наибольшее время, на
которое можно увеличить время работы,
если предшествующие
и последующие работы начинаются
в свои ранние
сроки.
работы ( i, j
) называется наибольшее время, на
которое можно увеличить время работы,
если предшествующие
и последующие работы начинаются
в свои ранние
сроки.
Коротко: "до нас и после нас рано".
Свободный резерв полностью определяется ранними сроками событий, не зависит от (это один из "внутренних" параметров проекта). Несложно получить (см. схему).
![]() ,
,
![]() ,
,
![]() .
.
Определение.
Частным резервом второго рода
![]() работы ( i, j
) называется наибольшее время, на
которое можно увеличить время работы,
если предшествующие и последующие
работы начинаются в свои поздние
сроки.
работы ( i, j
) называется наибольшее время, на
которое можно увеличить время работы,
если предшествующие и последующие
работы начинаются в свои поздние
сроки.
Коротко: "До нас и после нас поздно".
![]() ,
,
![]() ,
,
![]() .
.
Резерв второго рода – "внутренний" параметр (докажите это!).
Определение. Частным резервом
первого рода
![]() работы ( i, j
) называется наибольшее время, на
которое можно увеличить время работы,
если предшествующие
начинаются и заканчиваются в поздние
сроки, а последующие
– в ранние
сроки.
работы ( i, j
) называется наибольшее время, на
которое можно увеличить время работы,
если предшествующие
начинаются и заканчиваются в поздние
сроки, а последующие
– в ранние
сроки.
Коротко: "до нас поздно, после нас рано".
![]() .
.
Условия в определении этого резерва часто не выполняются, так как в случае, когда предшествующие работы заканчивались поздно, следующие за ( i, j ) могут уже не иметь возможности начинаться рано. Формально в этом случае частный резерв первого рода является отрицательным и показывает не запас, а нехватку времени для работы. В литературе встречается формула
![]() .
.
В любом случае справедливы соотношения
![]() ,
,
![]() ,
,
т.е.
![]() наименьший среди резервов.
наименьший среди резервов.
Частный резерв первого рода – "внешний" параметр.
Из расчётных формул для резервов можно получить полезное соотношение
![]() ,
,
позволяющее вычислить любой из резервов, если остальные три известны. Приведём полную таблицу параметров работ в примере 1.
Временные параметры работ Таблица 6.
Работа |
Обознач. |
Время |
|
|
|
|
|
|
|
|
|
|
B |
( 1, 2 ) |
13 |
|
0 |
13 |
19 |
6 |
|
6 |
0 |
3 |
-3 |
D |
( 1, 3 ) |
12 |
|
0 |
12 |
15 |
3 |
|
3 |
0 |
0 |
-3 |
H |
( 1, 4 ) |
6 |
|
0 |
6 |
15 |
9 |
|
9 |
6 |
6 |
3 |
F |
( 2, 5 ) |
1 |
|
13 |
14 |
20 |
19 |
|
6 |
0 |
0 |
-6 |
I |
( 2, 7 ) |
5 |
|
13 |
18 |
25 |
20 |
|
7 |
0 |
1 |
-6 |
G |
( 3, 6 ) |
5 |
|
12 |
17 |
22 |
17 |
|
5 |
0 |
2 |
-3 |
C |
( 4, 7 ) |
10 |
|
12 |
22 |
25 |
15 |
|
3 |
0 |
0 |
-3 |
A |
( 5, 6 ) |
2 |
|
14 |
16 |
22 |
20 |
|
6 |
1 |
0 |
-5 |
E |
( 6, 7 ) |
3 |
|
17 |
20 |
25 |
22 |
|
5 |
2 |
0 |
-3 |

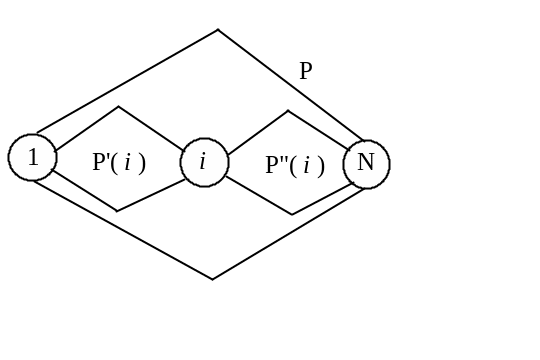 Рис.
12.
Рис.
12.