1. Магнитное поле в веществе

1.1. Намагничивание вещества

Если в магнитное поле внести образец какого-либо вещества, то он будет определённым образом взаимодействовать с этим полем: ориентироваться, втягиваться в область более сильного поля или выталкиваться из неё. Кроме того, магнитное поле изменится как вне образца, так и внутри него. Это связано с тем, что всякое вещество является магнетиком, т.е. способно под действием магнитного поля приобретать магнитный момент – намагничиваться. Причина намагничивания вещества заключается в следующем.

Молекулы многих веществ обладают собственными магнитными моментами, включающими в себя орбитальные и спиновые магнитные моменты электронов. Такие вещества называются парамагнетиками. Каждому молекулярному магнитному моменту можно сопоставить некоторый элементарный круговой ток, создающий в окружающем пространстве магнитное поле. Такие элементарные токи называются молекулярными токами. При отсутствии внешнего магнитного поля магнитные моменты молекул ориентированы беспорядочно, и суммарный магнитный момент вещества равен нулю. Если же образец вещества поместить во внешнее поле, то под его воздействием молекулярные магнитные моменты приобретают преимущественную ориентацию в одном направлении – вдоль внешнего поля, и суммарный магнитный момент образца становится отличным от нуля – вещество намагничивается.

В некоторых веществах молекулы не имеют собственного магнитного момента в отсутствие внешнего поля, так как векторная сумма всех орбитальных и спиновых магнитных моментов их электронов оказывается нулевой. Такие вещества называются диамагнетиками. Однако внесение таких веществ в магнитное поле индуцирует элементарные токи в молекулах; у молекул появляются магнитные моменты, ориентированные преимущественно в одном направлении, в данном случае – против внешнего поля. Следовательно, образец такого вещества также приобретает магнитный момент, т.е. намагничивается.

Степень намагничивания вещества характеризуется вектором намагниченности М. Он определяется как магнитный момент единицы объёма вещества, под которым понимается векторная сумма всех молекулярных магнитных моментов р_m в единице объёма. Если среднее число молекул в единице объёма равно п (средняя концентрация молекул), а их средний магнитный момент равен <р_m>, то намагниченность

М=п<р_m>= .

1.2. Магнитное поле в веществе и вектор н

Упорядочение молекулярных токов при внесении образца во внешнее магнитное поле В₀ порождает дополнительное поле В', которое, складываясь с В₀, даёт результирующее магнитное поле В в веществе и окружающем его пространстве:

В=В₀+В'. (1)

Но поскольку истинное магнитное поле в каждой точке вещества (микрополе), определяемое формулой Лоренца F=q(υ×B), резко непостоянно в пределах межъядерных расстояний как в пространстве, так и во времени, то под величинами В' и В в формуле (1) понимается поле, усреднённое по некоторому объёму вещества ΔV (макрополе). Этот объём должен быть достаточно мал, с тем чтобы имело смысл говорить о локальном значении поля В в данном месте вещества, и в то же время он должен содержать достаточно много молекул, чтобы имела смысл операция усреднения.

Поскольку магнитное поле в веществе В, определяемое формулой (1), создаётся как внешними источниками – токами проводимости, текущими по проводам, так и внутренними – эквивалентными молекулярными токами, то теорему о циркуляции вектора В можно записать в виде:

, (2)

где μ₀=4π·10⁻⁷ Гн/м – магнитная постоянная, i и i' – токи проводимости и молекулярные токи, «нанизанные» на выбранный контур обхода С. Можно показать, что с молекулярными токами i' связана циркуляция вектора М:

. (3)

Полагая контур С в уравнениях (2) и (3) одним и тем же, получим:

.

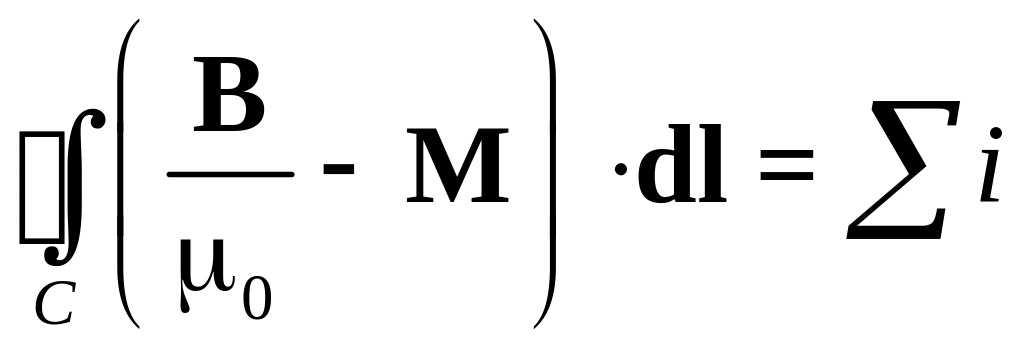Величину в скобках удобно обозначать вектором Н, т.е.

Н= , (4)

тогда

. (5)

Формула (5) выражает теорему о циркуляции вектора Н: циркуляция вектора Н по произвольному контуру С равна алгебраической сумме токов проводимости (свободных токов), охватываемых этим контуром.

Вектор Н, выражаемый комбинацией двух различных величин (4), − это вспомогательный вектор, не являющийся самостоятельной характеристикой поля или состояния вещества. Однако его использование часто оказывается удобным в связи с тем, что он, в силу (5), определяется только свободными токами в намагничивающей обмотке (и поэтому поле Н часто называется намагничивающим полем). А так как для всех ферромагнитных материалов зависимости В(Н) хорошо измерены, то для определения магнитного поля В в веществе, а также намагниченности вещества может оказаться достаточным лишь измерить ток намагничивающей обмотки.