Вязкость растворов высокомолекулярных соединений. Определение молекулярной массы полимеров по вязкости их растворов

Цель работы: определение вязкости растворов высокомколекулярных соединений (ВМС) различной концентрации и расчет его молекулярной массы по уравнению Марка − Куна − Хаувинка.

Общие теоретические положения

Основы теории вязкости разбавленных лиозолей (суспензий) были заложены Эйнштейном. Он исходил из гидродинамических уравнений для макроскопических твердых сферических частиц, которые при сдвиге приобретают дополнительное вращательное движение. Рассеяние энергии при этом является причиной возрастания вязкости. Эйнштейном была установлена связь между вязкостью дисперсной системы ŋ и объемной долей дисперсной фазы :

ŋ = ŋ₀ (1+2,5 ), (6.1)

где ŋ₀ — вязкость дисперсионной среды.

При выводе этого уравнения предполагалось, что система несжимаема, отсутствуют скольжение между частицами и жидкостью, турбулентность и взаимодействие между частицами. Неоднократные экспериментальные проверки уравнения Эйнштейна в основном подтвердили его справедливость. Было установлено, что коэффициент при зависит от формы частиц. Поэтому уравнению Эйнштейна можно придать более общий вид:

ŋ = ŋ₀ (1+ ), (6.2)

где α - коэффициент, зависящий от формы частиц дисперсной фазы.

Из теории Эйнштейна следует, что разбавленные и устойчивые дисперсные системы являются ньютоновскими жидкостями, что их вязкость линейно связана с объемной долей дисперсной фазы и не зависит от дисперсности.

Теория Эйнштейна была использована Штаудингером для установления формулы вязкости разбавленных растворов полимеров. Вязкость растворов ВМС при идентичных условиях (одинаковый состав, равная концентрация и температура) может быть переменной. Поэтому ее сопоставляют с вязкостью чистою растворителя.

Для характеристик связи между вязкостью дисперсной системы ŋ и вязкостью дисперсионной среды ŋ₀ используют ряд величин.

Относительную вязкость ŋ_от можно определить по времени истечения раствора ВМС через калиброванное отверстие вискозиметра

(6.3)

где τ и τ₀ - время истекания из вискозиметра раствора ВМС и дистиллированной воды соответственно.

Последнее соотношение легко получить из уравнения Пуазейля

(6.4)

учитывая, что ∆р = gρ∆h и ρ ≈ ρ₀, где V − объемная скорость течения (истечения) жидкости; r − радиус капилляра; ∆р − перепад давлений, вызывающий движение жидкости; l − длина капилляра; g = 9,81 м/с² − ускорение свободного падения; ∆h − высота столба жидкости; ρ и ρ₀ − плотности частиц дисперсной фазы и дисперсионной среды соответственно.

Удельная вязкость ŋ_уд, показывающая на сколько увеличилась вязкость ВМС по сравнению с вязкостью растворителя, определяется по выражению

(6.5)

Использование приведенной вязкости ŋ_пр обусловлено зависимостью конформации и ориентации макромолекул (относительно направления течения раствора) от концентрации. Она определяется соотношением

(6.6)

где ω − концентрация ВМС, выраженная в массовых долях.

Приведениям вязкость, экстраполированная к бесконечному разведению, т.е. рассчитанная для условий, исключающих взаимодействие части дисперсной фазы между собой, называется характеристической вязкостью [ŋ] дисперсной системы:

(6.7.)

Приведенная вязкость обычно линейно зависит от концентрации ВМС. Поэтому на практике значение характеристической вязкости определяют как отрезок на оси ординат, получаемый экстраполяцией зависимости

По Штаудингеру, для растворов, содержащих палочкообразные макромолекулы, должно соблюдаться соотношение

(6.8.)

где К — константа, характерная для данного полимергомологического ряда в данном растворителе; М_r —молекулярная масса полимера.

По представлениям Штаудингера, чем больше длина молекулы полимера, тем больший объем вращения она имеет и тем больше вязкость раствора (при одной и той же концентрации ω.

Уравнение (6.8) используют для определения молекулярной массы полимеров. Константу К определяют независимым методом, например но значению молекулярной массы низкомолекулярных членов полимер гомологического ряда, найденной криоскопическим методом. Молекулярную массу определяют по графической зависимости

Уравнение Штаудингера (6.8) справедливо только для растворов полимеров с короткими и жесткими цепями, которые могут сохранять палочкообразную форму.

Гибкие молекулы полимеров, имеющие длинные цепи, обычно свертываются в клубок, что уменьшает сопротивление их движению. При этом К изменяется и зависимость вязкости от молекулярной массы оказывается нелинейной.

В последнем случае более правильно связывать с молекулярной массой полимера характеристическую вязкость [ŋ], так как именно этой величиной оценивается прирост вязкости раствора, вызванный наличием макрочастиц и их вращением.

Наиболее широкое распространение для определения молекулярной массы полимеров получило соотношение Марка — Куна — Хаувинка, иногда называемое также обобщенной формой уравнения Штаудингера

(6.9)

где К - константа, характерная для данного гомологического ряда, зависящая от взаимодействия молекул ВМС с растворителем; а- величина, зависящая от гибкости полимера и изменяющаяся от 0,5 до 1.

Исходя из соотношения (6.9) молекулярную массу ВМС можно рассчитать но выражению

(6.10)

Вязкость растворов полимеров до концентраций 10-20 масс.% удовлетворительно описывается уравнением Мартина:

(6.11)

или в логарифмической форме

(6.12)

Исходя из выражения (6.12), по зависимости

можно определить величину ln [ŋ] (отрезок, отсекаемый на оси ординат), а следовательно, и характеристическую вязкость.

ПРИБОРЫ И РЕАКТИВЫ:

Вискозиметр Оствальда.

Секундомер.

Технохимические весы.

Мерный цилиндр объёмом 10 и 50 мл.

Электроплита.

Конические колбы или химические стаканы объёмом 50 мл, 5 шт.

Дистиллированная вода.

Желатин.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:

Для проведения настоящей работы используют капиллярный вискозиметр Оствальда (рис. 6.1).

В правое колено вискозиметра впаян капилляр 1, соединенный с полым шариком 2. Левое колено представляет собой широкую трубку, заканчивающуюся емкостью 3. Назначение емкости 3 состоит в том, чтобы поддерживать по возможности постоянным уровень жидкости в левом колене. В левое колено прибора через воронку наливают исследуемую жидкость, причем уровень жидкости не должен быть выше середины емкости 3.

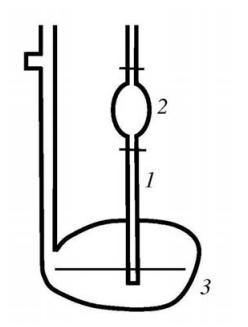
Рис. 6.1. Капиллярный вискозиметр Оствальда

Необходимо проверить вертикальность положения прибора. Жидкость при закрытом пальцем левом колене засасывают с помощью резиновой груши в правое колено настолько, чтобы ее верхний мениск оказался несколько выше верхней метки над расширителем 2, и дают жидкости свободно вытекать из правою колена. Секундомером измеряют время прохождения мениска жидкости от верхней метки до нижней.

При выполнении лабораторной работы вискозиметр калибруют по чистому растворителю (дистиллированная вода). Время прохождения мениска жидкости между метками измеряется несколько раз, причем расхождение между измерениями не должно быть более 0,2 с.

Для проведения работы первоначально готовят 100 мл 1% водного раствора желатина, т. е. в этом растворе = 0,01. Для этого отвешивают 1 г желатина, помещают в колбу и доливают холодной дистиллированной водой до 100 мл. После выдержки в течение 0,5 часа для набухания желатина проводят его растворение при нагревании и постоянном перемешивании. Полученный прозрачный раствор охлаждают до комнатной температуры. Из 50 мл исходного раствора методом последовательного разбавления вдвое готовят еще три раствора. При этом во всех случаях 50 мл полученного раствора оставляют для измерения, а 50 мл используют для получения следующего раствора (помещают в чистую колбу, добавляют 50 мл дистиллированной воды и перемешивают).

Первоначально проводят калибровку вискозиметра по чистому растворителю. По пяти измерениям определяют среднее время истечения воды, которое в последующих расчетах принимают за τ₀. Данные по определению среднего времени истекания воды сводят в таблицу 6.1.

Таблица 6.1.

Определение среднего времени истекания воды

№ опыта	Время истекания воды, с	Среднее время истекания воды τ0, с
1
2
3
4
5

Определяют время истекания четырех приготовленных водных растворов желатина и рассчитывают ŋ_отн, ŋ_уд, ŋ_пр [соответственно по уравнениям (6.3), (6.5), (6.6)] и lnŋ_пр. Полученные результаты сводят в таблицу 6.2.

Таблица 6.2.

Экспериментальные данные по времени истекания растворов желатина и расчетные величины

Концентрация раствора желатина 102	1	0,5	0,25	0,125
Время истекания раствора желатина τ, с	1. 2. Среднее	1. 2. Среднее	1. 2. Среднее	1. 2. Среднее
ŋотн[уравнение (6.3)]
ŋуд[уравнение (6.5)]
ŋпр[уравнение (6.6)]
lnŋпр

По полученным результатам строят графики зависимостей

По графикам определяют значения характеристической вязкости [ŋ] и ее натурального логарифма (как отрезки, отсекаемые на осях ординат). Понятно, что, зная величину ln[ŋ], легко определить значение [ŋ].

Величину молекулярной массы желатина находят по уравнению (6.10), используя значения [ŋ], полученные по зависимости

Для водного раствора желатина при 20 °С К = 3,0∙10^-4, а = 0,67.

Лабораторная работа №7.