9. Характеристики линейного звена.

САУ удобно представлять для анализа и при синтезе в виде взаимосвязанной совокупности отдельных элементов – динам. звеньев.

Под динам. звеном понимают в общем случае абстрактное устройство, имеющее вход и выход, и для которого задано уравнение, связывающее сигналы на входе и выходе, как это показано на рис.

Динам. звенья описывают в виде нелин. диф. уравнений. Но во многих случаях их можно линеаризовать, то есть заменить нелинейные уравнения линейными, приближенно описывающими процессы в системах.

Такому подходу способствует то, что, в большинстве случаев, нормально функционирующая система работает в режиме малых отклонений, при которых нелинейности не проявляются.

Если уравнение, связывающее сигналы X_вх(t) и X_вых(t), линейно, то говорят о линейном динамическом звене.

Уравнение линейного динамического звена имеет следующий общий вид:

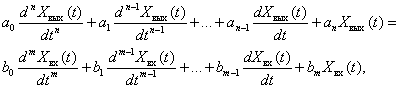
где a₀…a_n, b₀…b_n - постоянные коэффициенты, m≤n .

Основные характеристики линейных звеньев:

• переходная характеристика h(t) - реакция звена на ступенчатое единичное воздействие 1(t);

• передаточная функция W(s), связывающая изображения входного X(s) и выходного Y(s) сигналов линейного звена;

• комплексный коэффициент передачи W(jw), связывающий спектры входного X(jw) и выходного Y(j) сигналов линейного звена и

• импульсная или весовая функция w(t) реакция звена на дельта-функцию Дирака (t).

1. Переходная функция (характеристика) звена

Сигнал, полученный на выходе звена, при подаче на вход единичного скачка называется переходной функцией звена и обозначается h(t). Переходная функция однозначно связана с передаточной функцией: h(t)=L^-1[W(p)/p],

где L^-1 – оператор обратного преобразования Лапласа.

Подставив в выражение представление передаточной функции как частное двух полиномов W(p)=K(p)/D(p), и перейдя от изображения к оригиналу, получим следующее выражение для определения переходной функции:

,

где p_i – это корни уравнения D(p)=0, т.е. полюса передаточной функции.

Переходную функцию удобно представить в виде суммы двух составляющих - свободной и вынужденной. Вынужденная составляющая h_вын = h(¥) = K(0)/D(0),

характеризует состояние объекта после того, как все переходные процессы, начавшиеся в системе после подачи на вход единичного скачка, закончились. Свободная составляющая

h_св = h(t) - h(¥), характеризует переходный процесс, возникший в системе после подачи на вход единичного скачка.

2. Передаточная функция

Отношение изображения по Лапласу выходного сигнала линейного звена к изображению по Лапласу входного сигнала, при нул. нач. условиях, называют передаточной функцией линейного звена: .

Для рассматриваемых в ТАУ систем, справедливо выражение: m£n. Если вместо комплексной переменной p подставить в выражение для W(p) чисто мнимое выражение jw, то получим комплексный коэффициент передачи W(jw).

3. Комплексный коэффициент передачи

Комплексный коэффициент передачи линейного звена – это отношение комплексной амплитуды сигнала, снимаемого с выхода звена, к комплексной амплитуде сигнала, поданного на его вход:

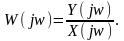(2.5)

Комплексный коэффициент передачи часто используют для графического представления свойств звена. Для этого строят частотный годограф. Частотный годограф – это геометрическое место точек, конца вектора комплексного коэффициента передачи, при изменении w от 0 до ¥. Пример частотного годографа представлен на рис. Следует отметить, что если справедливо выражение m<n, то годограф при w®¥ , будет стремиться к началу координат.

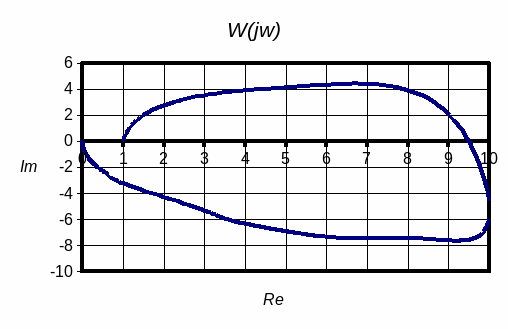
Рис. Пример частотного годографа.

В ряде случаев вместо одной кривой – частотного годографа, строят две кривые:

- амплитудно-частотную характеристику звена (АЧХ), которая демонстрирует зависимость модуля комплексного коэффициента передачи от частоты: A(w)=|W(jw)|;

- фазочастотную характеристику звена (ФЧХ), которая демонстрирует зависимость фазы (иными словами аргумента) комплексного коэффициента передачи от частоты:

j(w) =argW(jw).

При построении АЧХ и ФЧХ, может быть использован логарифмический масштаб. Такие характеристики называют:

логарифмическими амплитудно-частотными (ЛАЧХ): L(w)=20 lg|W(lgw)|,

логарифмическими фазочастотными характеристиками (ЛФЧХ): F(w)=j(lgw).