
- •Розрахунок основних характеристик системи передачі
- •Техническое задания на систему связи
- •Введение
- •1 Анализ источника сообщений
- •1.1 Вероятностный анализ
- •1.2 Временной анализ
- •1.3 Частотный анализ
- •1.4 Информационный анализ
- •2 Расчет ацп
- •3 Расчет кодера
- •4 Расчет модулятора
- •5 Анализ канала связи
- •6 Расчет оптимального когерентного демодулятора
- •7 Анализ декодера
- •8 Расчет цифро-аналогового преобразователя
- •Заключение
- •Список литературы
2 Расчет ацп
Для преобразования любого аналогового сигнала в цифровой необходимо выполнить две основные операции: дискретизацию и квантование. Процесс дискретизации по времени – это процесс получения мгновенных значений преобразуемого аналогового сигнала с определенным временным шагом, называемым шагом дискретизации. Квантование – процесс округления значений сигнала до ближайшего уровня.
Шаг дискретизации по времени ∆t определим из теоремы Котельникова:
 (6)
(6)
Шаг квантования по уровню определяем от уровня помехи сигнала. Дисперсия помехи сигнала равна
N* fmax=0,55*107 В2/Гц*10000 Гц=5,5*10-4 B2, (7)
а СКО=2,34*10-2 B. Число уровней квантования L при равномерном шаге
Δx=3*CKO=0,07 В (8)
определятся как частное от деления размаха сигнала (хmax-хmin) на шаг квантования Δх.
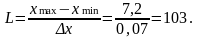 (9)
(9)
Ближайшее кратное степени 2 является 128, т.е. разрядность АЦП равна не менее 7.
Для нахождения средней мощности шума квантования надо знать закон распределения шума – pАЦП(ξ.) Так как мгновенные значения равновероятны в заданном интервале, то закон распределения шума pАЦП(ξ.) в интервале xj-Δx/2≤ξ≤xj+Δx/2 (где xj-jй уровень квантования) будет равномерным и не будет зависеть от номера интервала.
Следовательно, средняя мощность шума квантования будет равна:
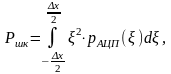 (10)
(10)
Закон распределения шума определим из условия нормировки:
 (11)
(11)
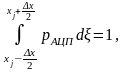 (12)
(12)
 (13)
(13)
Тогда плотность распределения имеет вид
 (14)
(14)
Средняя мощность шума квантования:
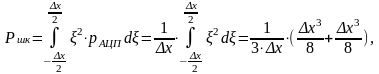 (15)
(15)
 (16)
(16)
Определим относительную величину мощности шума квантования по сравнению с мощностью переменной составляющей сигнала
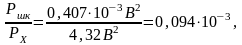 (17)
(17)
 (18)
(18)
Число двоичных
разрядов k, требуемое для записи любого
номера из L уровней квантования
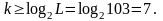
Номеру квантования j = 103 соответствует двоичное число 1100111 и уровень сигнала
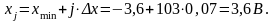 (19)
(19)

Рисунок 8 – Временная диаграмма отклика АЦП (дискретизатора) на уровень с номером j = 103.
Энтропия – это математическое ожидание количества информации или мера неопределенности сообщений.
Покажем, что при заданном законе распределения мгновенных значений процесса x(t) все уровни квантования равновероятны. Для этого найдем вероятность j-го уровня квантования, что равносильно вероятности попадания x(t) в интервал xj≤x≤xj+1.
 (20)
(20)
Мы видим, что P(xj) не зависит от j.
Тогда энтропия будет определяться как энтропия дискретного источника независимых сообщений, все символы которого равновероятны. Производительностью такого источника будет суммарная энтропия сообщений, переданных за единицу времени:
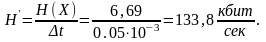 (21)
(21)
Графики цифрового сигнала и спектральной плотности мощности этого сигнала.

Рисунок 8 – Оцифрованный сигнал
 Рисунок
9 – Оценка энергетического спектра
цифрового сигнала
Рисунок
9 – Оценка энергетического спектра
цифрового сигнала
Из рисунка 9 видно, что проявился эффект «размножения» частот, вызванный дискретизацией аналогового сигнала.
