
- •Розрахунок основних характеристик системи передачі
- •Техническое задания на систему связи
- •Введение
- •1 Анализ источника сообщений
- •1.1 Вероятностный анализ
- •1.2 Временной анализ
- •1.3 Частотный анализ
- •1.4 Информационный анализ
- •2 Расчет ацп
- •3 Расчет кодера
- •4 Расчет модулятора
- •5 Анализ канала связи
- •6 Расчет оптимального когерентного демодулятора
- •7 Анализ декодера
- •8 Расчет цифро-аналогового преобразователя
- •Заключение
- •Список литературы
1.1 Вероятностный анализ
Функция распределения в теории вероятности – функция, которая характеризует распределение случайной величины или случайного вектора.
Функция распределения:
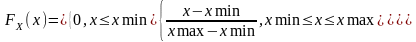 (1)
(1)

Рисунок 2 – График функции распределения
Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.
Функция плотности распределения:
 (2)
(2)

Рисунок 3 – График функции плотности распределения
Математическое ожидание и дисперсия сигнала.
Диапазон
сигнала
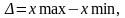 тогда
тогда
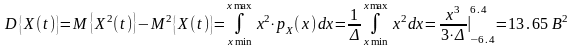 (3)
(3)
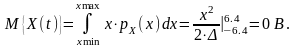 (4)
(4)
Рассматриваемый
случайный процесс является эргодическим
– усреднение какой – либо одной его
реализации равно усреднению ансамбля
(множества) реализаций. Для эргодического
процесса математическое ожидание
характеризует постоянную составляющую,
а дисперсия – мощность переменной
составляющей. Спектральная плотность
средней мощности имеет равномерное
распределение величины
 .
Тогда X̅=0 – постоянная составляющая
сигнала источника, а Px=13,65
B2
– мощность переменной составляющей
сигнала.
.
Тогда X̅=0 – постоянная составляющая
сигнала источника, а Px=13,65
B2
– мощность переменной составляющей
сигнала.
Оценки математического ожидания и дисперсии сигнала
>>m_SIG=mean(SYG)
МО=-0,0694В,
>>std_SIG=std(SYG)
СКО=2.1250В.
Оценка корреляционной функции сигнала
>>Kx=XCOV(SYG,'biased');
>>tau=((0:N/8))*Ts;
>>plot(tau,Kx(N:N+N/8))
Корреляция (от латинского сorrelatio – соотношение, взаимосвязь) корреляционная зависимость – статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.

Рисунок 4 – График корреляционной функции
1.2 Временной анализ
Временной анализ заключается в оценке и определении временных характеристик сигнала, для чего строим график исходного сигнала. График представлен на рисунке 5.

Рисунок 5 – Исходный сигнал
1.3 Частотный анализ
 Рисунок
6 – Оценка энергетического спектра
сигнала
Рисунок
6 – Оценка энергетического спектра
сигнала
 Рисунок
7 – Оценка спектральной плотности
мощности сигнала
Рисунок
7 – Оценка спектральной плотности
мощности сигнала
Из рисунка 7 определяем практическую ширину спектра сигнала fmax = 8 кГц.
1.4 Информационный анализ
Для большинства реальных источников сообщения имеют разные вероятности. Например, в тексте буквы А, О, Е встречаются сравнительно часто, а Щ, Ы – редко. При разных вероятностях сообщения несут различное количество информации . При решении большинства практических задач необходимо знать среднее количество информации, приходящееся на один элемент сообщения. Это среднее количество информации при общем числе элементов сообщения источника n и числе символов алфавита
Термин «энтропия» заимствован из термодинамики, где она характеризует среднюю неопределенность состояния системы молекул вещества. В теории информации этот термин введен в 1948 г. американским ученым К. Шенноном и далее более строго определен советскими математиками А.Я. Хинчиным и А.Н. Колмогоровым. Физически энтропия выражает среднюю неопределенность состояния источника сообщений и является объективной информационной характеристикой источника. Энтропия всегда положительна и принимает максимальное значение при равновероятных сообщениях.
Минимальное значение энтропии 0 соответствует случаю, когда одна из вероятностей равна 1, а остальные равны нулю, т.е. имеется полная определенность [интернет].
Определим дифференциальную энтропию сигнала – источника сообщений:
 (5)
(5)
