Расчет лесов конструкции вниомс на устойчивость

В лесах конструкции ВНИОМС на хомутах, как было сказа­но выше, все вертикальные нагрузки передаются с поперечин на стойки с одной стороны стойки через соединительный хомут.

Под действием опорного момента, приложенного в узле стой­ка в ярусе получает некоторый прогиб в плоскости действия мо­мента. Продольная сжимающая сила создает на месте прогиба Дополнительный изгибающий момент, влияние которого на ра­боту стойки при достаточной ее гибкости может оказаться весь­ма существенным при превышении продольной силой предель­ных значений.

Стойки этих лесов собирают из элементов длиной 4 м (кроме нижнего, длина которого может быть равна 2 м).

При производстве каменных работ с применением лесов на элемент стойки может передаваться только один сосредоточен­ный опорный момент от временной нагрузки на рабочем настиле. Этот момент может быть приложен либо в верхнем узле стойки, либо в среднем. Наиболее невыгодно его приложение в верхнем узле.

В лесах конструкции ВНИОМС на хомутах потеря устойчи­вости может иметь место в плоскости действия момента и из плоскости действия момента.

Рассмотрим эти два случая.

Общий случай работы одного загруженного яруса стойки показан на рис. 50. На элемент стой­ки действует продольная сжимающая сила Р, мо­менты, приложенные в узлах MI и М2, и попереч­ные силы Q от моментов как реакции продольных связей. Под действием опорных моментов, направ­ленных так, что они изгибают стойку в одну сто­рону, стоика прогибается в середине на величину у. Сжимающая сила Р создает дополнительный изги­бающий момент в плоскости действия опорных мо­ментов.

Рис. 50. Общий случай продольного изгиба стойки

Согласно рис. 50 напишем выражение для изгибающего момента в любом сечении х рассматриваемого яруса стойки:

M_x = M₂ + Q_x + P_y.

Для нахождения максимального изгибающего момента нуж­но составить дифференциальное уравнение, которое в общем ви­де записывается так:

где Е— модуль упругости;

у" — вторая производная от прогиба у по длине стержня;

J — момент инерции стержня.

Подробное решение этого дифференциального уравнения из­ложено в книге Н. Д. Золотницкого и П. Ф. Дроздова «Условия безопасной работы на металлических лесах» (Изд-во МК.Х РСФСР, 1951).

В результате получено общее выражение величины макси­мального момента

где

h — высота яруса;

M₂ — меньший по абсолютной величине опорный момент;

e₁ и е₂ — условные эксцентриситеты приложения продольной силы.

α изменяется от +1 до -1 (при двустороннем расположении по­перечин).

Если M₂ = 0, то α = 0 (в нижнем ярусе стойки)

где е₀ = 7,2 см.

Вместе с тем из решения дифферен­циального уравнения сделан вывод, из которого следует, что изгибающий мо­мент в любом сечении стойки данного яруса не превысит величины опорного момента, пока сжимающая сила Р не превысит значения четверти критической силы:

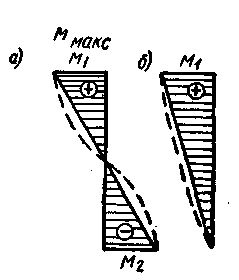
Рис. 51. Предельные случаи отношения моментов в ярусе

где Р_э — эйлеровская критическая сила.

В лесах на хомутах при одностороннем расположении поперечин, передающих опорные моменты на стойку, α изменяется от -1 до 0.

При равенстве абсолютных значений опорных моментов α = -1 и эпюра моментов стойки имеет вид, представленный на рис. 51, а. При отсутствии опорного момента в нижнем узле (М₂=0) эпюра моментов имеет вид, представленный на рис. 51,б. Здесь пунктирная кривая учитывает дополнительные моменты от продольной силы на прогибах стойки от основных и опорных моментов.

Из решения дифференциального уравнения также следует, что отношение условных эксцентриситетов

но , следовательно, и превышение М_mах над опорным моментом в пределах данного яруса может иметь место либо при возрастании α, когда costh постоянен, либо при уменьшении costh, когда постоянно α. Отсюда вытекает условие

M_max ≥M_оп, когда α ≥ cos th

Когда α < cos th, наибольшим действительным изгибающим мо­ментом в сечениях стойки будет больший из опорных моментов.

Это именно то условие, которое требуется выяснить расчетом при рассмотрении устойчивости стойки в плоскости действия опорных моментов.

Прежде чем перейти к расчетной проверке, преобразуем вы­ражение cos th.

Поскольку

где Р_расч — расчетная сжимающая сила. Тогда условие будет выражено:

М_max ≥ М_оп, когда

М_max ≤ М_оп, когда

Проверка устойчивости лесов в плоскости действия момен­тов. Реакция стойки от временной нагрузки Р_вр или усилие по расчету (см. рис. 46,6) составит:

Р_вр=К_А =910 кГ.

Постоянная нагрузка без учета собственного веса стойки со­ставляет 118,4 кГ.

Тогда Р = Р_вр + Р_пост = 910 + 118,4 = 1028 кГ.

где Р_э = 12 900 кГ (табл. 41);

К = 2 — двойной коэффициент перегрузки.

Таблица 41

Расчетные величины для водогазопроводных труб
наружный диаметр в мм	толщина стенки в мм	вес 1 м в кг	площадь сечения в см2	момент инерция J в см4	момент сопро­тивления W в см3	критическая сила Рэ в кг
48 60	3,5 3,5	3,84 4,88	4,89 6,22	12,16 24,92	5,06 8,3	6300 12900

При этой величине продольной силы Р максимальным яв­ляется опорный момент. Проверим по условию

кГ·см

При М₂ = 0, α = 0

α < 0,342 и M_max = М_оп = 7401 кГ·см.

В этом случае сохраняется пропорциональность напряжения на­грузкам и проверку расчета лесов производят по допускаемым напряжениям

кГ/см²

В нижнем ярусе продольная сжимающая сила стойки скла­дывается из временной нагрузки, собственного веса металличе­ских элементов и веса настила:

кГ

где n =10 — число ярусов.

где К — двойной коэффициент перегрузки. В этом случае, как и в предыдущем, нет необходимости прове­рять устойчивость стоек на продольный изгиб. Но если высота лесов достигает 40 м, а число ярусов 20, в этом случае

Тогда производим проверку устойчивости нижней стойки на продольный изгиб с центральным приложением сжимающей си­лы (с учетом гибкости стойки).

Как уже определили выше для труб диаметром 60/53 мм, ра­диус инерции i = 2 см, а гибкость λ = 100. Соответственно коэф­фициент продольного изгиба φ = 0,6.

Тогда

Стойки лесов отвечают требованиям устойчивости даже при коэффициенте перегрузки, равном 2.

Проверка устойчивости лесов в, направлении, перпендику­лярном плоскости действия моментов. Если в плоскости дей­ствия моментов обеспечена несмещаемость узловых соединений элементов в секции лесов, то при креплении лесов к конструкциям объектов в стыках стоек (например, через 4 м по высоте и по горизонтали в шахматном порядке) средние узлы элемен­тов стоек под действием продольной силы могут перемещаться в направлении, перпендикулярном плоскости действия опорных моментов при упругом сопротивлении связанных с ними элемен­тов. Элемент стойки в пределах двух ярусов начинает работать на продольный изгиб, как балка, сжатая продольной силой и имеющая упругую опору в середине пролета.

Упругость этой опоры измеряется вели­чиной отпора продольных связей прогибу рассматриваемой стойки.

Величина упругого отпора аз есть сила, вызывающая единичный прогиб в элемен­тах, оказывающих упругое сопротивление. Эта сила характеризует упругость проме­жуточной опоры (рис.52).

Верхний предел для критического зна­чения сжимающей силы получается при аб­солютной жесткости промежуточной опоры α =∞, когда стержень изгибается по двум полуволнам (рис. 52,а), и равен:

где

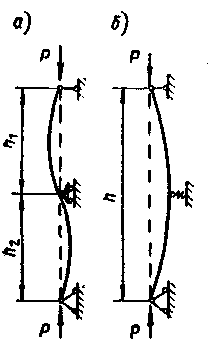
Рис. 52. Продольный изгиб стойки с упругой средней опорой

Нижний предел критической нагрузки получаем при условии, что промежуточная опора абсолютно по­датлива (α₂=0). Тогда изгиб стержня происходит по одной по­луволне (рис. 52, б):

Предельное значение жесткости промежуточной опоры, при котором стойка уже может изгибаться по двум полуволнам, оп­ределяется из уравнения

где — расстояние от промежуточной опоры до места наи­большего прогиба (см. рис. 52, а). Откуда

При всяких промежуточных значениях значе­ние критической силы будет находиться между верхним и ниж­ним пределами для данного стержня.

Существуют способы точного определения промежуточных значений критической силы, которые трудоемки и не исключают ошибок при вычислениях методом последовательных приближе­ний.

Для практических целей достаточно приближенного опреде­ления промежуточных значений критической силы по графику, приведенному на рис. 53.

При α₂ = 0 (одна полуволна) величина обращается в нуль и тогда

, а отношение Р_кр:Р_э = 1.

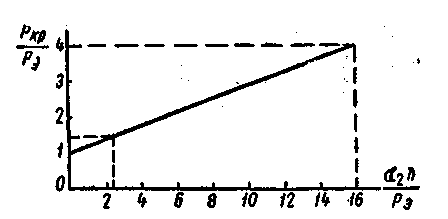
Рис. 53. График зависимости критической силы

от величины упругого отпора средней опоры

в двухъярусной стойке

При α₂ = α_2max (по двум полуволнам) = 16 и тогда

, а отношение Р_кр : Р_э = 4.

Для примера рассмотрим прогиб элемента стойки трубчатых лесов ВНИОМС длиной 4 м при упругом сопротивлении других элементов секции в среднем узле. Для этого выделим из карка­са лесов ячейку в виде системы связанных между собой стерж­ней, закрепленную в четырех точках к неподвижным опорам.

Возможная форма изгиба этой системы приведена на рис. 54 пунктиром. Каждая изгибаемая стойка испытывает упругое со­противление продольной связи.

В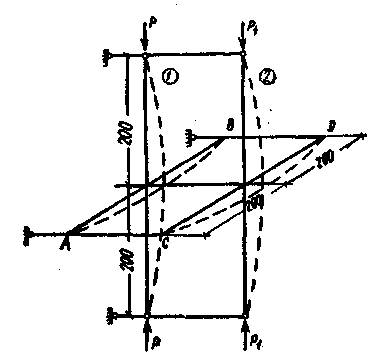 еличина упругого отпора неразрезной четырехметровой про­дольной связи определяется из условия

где δ — прогиб балки на двух опорах;

J — момент инерции.

кГ

Обращаясь к графику (рис. 53) и табл. 41, определим абс­циссу:

Рис.54. Продольный изгиб стоек в секции лесов

Этому значению соответствует отношение Р_кр : Р_э = 1,45 (см. рис. 53).

Тогда кГ.

Это почти в 1,5 раза больше предельного расчет­ного усилия в нижнем яру­се стойки лесов для камен­ных работ Р_расч = 3466 кГ (см. выше).

Следовательно, при по­становке креплений секции лесов к объекту в каждом стыке стоек устойчивость обеспечена.

В лесах конструкции ВНИОМС по техническим условиям крепления секций к объекту устанавливают через 6 л по высоте стойки и по горизонтали в шахмат­ном порядке. В этом случае стойка фактически работает под действием продоль­ной силы как трехпролетная балка с двумя промежуточными упругими опорами:

тогда верхний предел критической силы при абсолютной жест­кости упругих опор ( )

(где h = 600 см).

Соответственно при абсолютной податливости промежуточных опор ( )

Умножив обе части равенства на , получим

отсюда ,

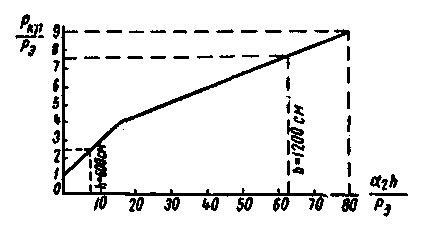
Рис. 55. График зависимости критической силы от величины упругого отпора средних опор в трех- и шестиярусных стойках

где β — числовой коэффициент, зависящий от числа пролетов стойки;

m — число пролетов.