Сводная таблица вероятностей базовых нардовых событий.
№ |
ВЕРОЯТНОСТЬ |
Доли |
%% |
1 |
Какой-либо конкретный куш |
1 /3 6 |
2,78% |
2 |
Какой-либо конкретный обычный бросок |
2 / 36 |
5,56% |
3 |
Какой-нибудь (любой) куш, не зависимо какой именно |
6 / 36 |
16,67% |
4 |
Обычный бросок - НЕ КУШ, какой-нибудь |
30 / 36 |
83,33% |
5 |
В броске будет какая-то конкретная цифра |
11 / 36 |
30,56% |
6 |
В броске НЕ будет какой-то конкретной (одной) цифры |
25 / 36 |
69,44% |
7 |
ДВА броска подряд ни разу НЕ выпадет конкретная цифра |
625/1296 |
48,23% |
8 |
В двух бросках подряд выпадет хотя бы одна конкретная цифра |
671/1296 |
51,77% |
9 |
Выпадет 4 или 6 (какая-то из двух заданных цифр) |
20 / 36 |
55,56% |
10 |
Выпадет 2, 4 или 6 (какая-то из трех заданных цифр) |
27 / 36 |
75,00% |
11 |
Выпадет два раза подряд один и тот же куш |
(1/36)^2 |
0,07716% |
12 |
Выпадет три раза подряд один и тот же куш |
(1/36)^3 |
0,00214% |
13 |
Выпадет четыре раза подряд один и тот же куш |
(1/36)^4 |
0,00006% |
14 |
Выпадет два раза подряд какой-нибудь куш (любой) |
(1/6)^2 |
2,78% |
15 |
Выпадет три раза подряд какой-нибудь куш (любой) |
(1/6)^3 |
0,46% |
16 |
Выпадет четыре раза подряд какой-нибудь куш (любой) |
(1/6)^4 |
0,07716% |
17 |
Выпадет какой-нибудь (любой) куш хотя бы один раз из двух подряд бросков? |
1-(5/6)^2 |
30,56% |
18 |
Выпадет какой-нибудь (любой) куш хотя бы один раз из трех подряд бросков? |
1-(5/6)^3 |
42,13% |
19 |
Выпадет какой-нибудь (любой) куш хотя бы один раз из четырех подряд бросков? |
1-(5/6)^4 |
51,77% |
Еще две интересные вероятности от Олега (ник os2006, данные с форума fpclub ):
В партии, с количеством ходов N, вероятность получить К кушей (например, куша 66) имеет вид: N! / (N-K)! / K! * 35^(N - K) / 36^N. Для средней партии в длинные нарды получим таблицу и график ниже:
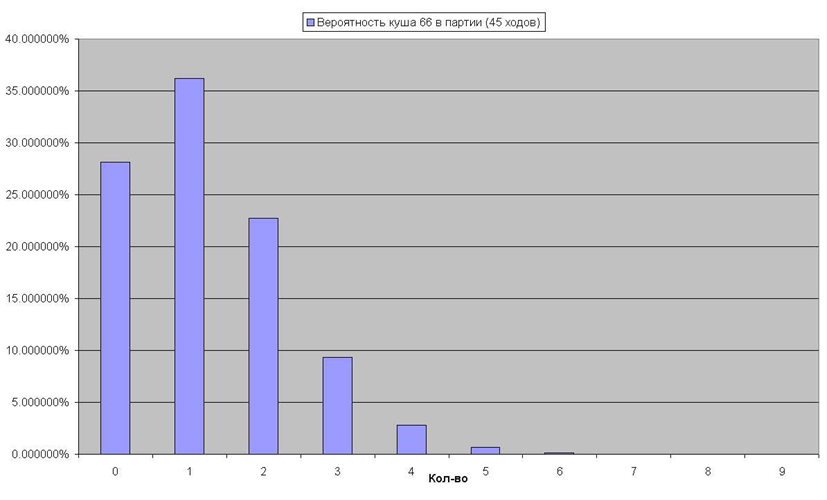
Также достойна внимания таблица:
Как часто партия должна заканчиваться с разницей в пипсах всего 10 (в пределах 1 броска)? А с разницей 20 пипсов? Смотрите ниже таблицу и график.
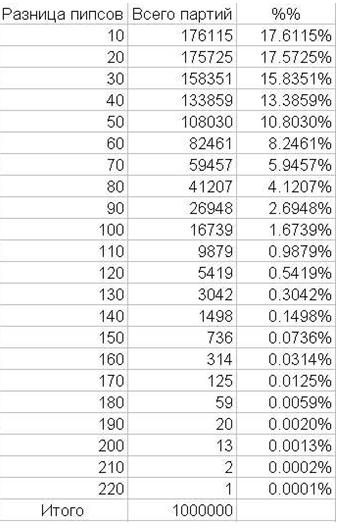
Пятая строка этой таблицы говорит о том, что каждая десятая партия должна заканчиваться с разницей в пипсах 50 очков. А первая строка должна вас приучить к тому, что примерно одинаково обоим игрокам (в пределах 10 пипсов разница) бывает только в каждой третьей партии. А в 2 из 3 партий разница будет больше.
Еще одна забавная цифра: если вы сыграете 200 партий, то 3 из них закончастя с разницей в пипсах около 100 очков.
Ну и, наконец, еще одна полезная таблица вероятностей.
Вероятность выбросить оставшиеся 2 шашки в самом конце игры:
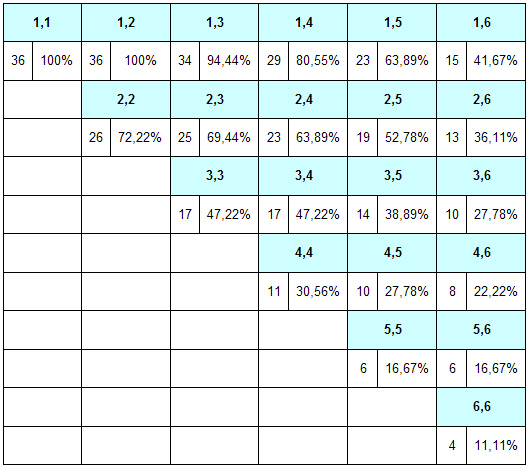
Для того, чтобы таблица стала понятнее, несколько картинок с шашками:
1,1 – две шашки на выброс в пункте 24 (последняя позиция доски для белых).
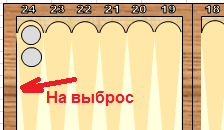
2,5 – одна шашка в пункте 23 (предпоследняя позиция) и одна в пункте 20.
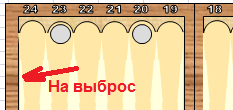
Взято с форума nardy.info.