- •Глава 1
- •Глава 2
- •2.3. Принципы уравнорешивания пространственных коленчатых валов
- •Глава 3
- •Глава 4
- •4.3. Расчетная оценка работоспособности элементов газового стыка
- •Глава 5 поршневая группа
- •Глава 6 шатунная группа
- •Глава 7 коленчатый вал
- •Глава 8
- •Глава 9
- •Глава 10 смазочная система
- •10.3. Схемы смазочных систем
- •Глава 11 система охлаждения
- •11.2. Регулирование производительности системы жидкостного охлаждения
- •113. Конструкция радиаторов
- •Глава 12 система воздухопитания
- •Глава 13 система выпуска
- •Глава 14 система пуска двигателей
- •Глава 15
- •Глава 1. Кивематика я динамика кривошиино-шатуиного механизма ... 5
- •Глава 2. Уравновешенность я уравновешивание двигателей внутреннего сгора-
- •Глава 5. Порпневая груша 121
- •Глава 6. Шатунная груша 155
- •Глава 7. Коленчатый вал 170
- •Глава 8. Колебания в двмателях внутренвего сгорания 185
- •Глава 9. Механзм газораспределения 221
- •Глава 10. Смазочная система 272
- •Глава 11. Система охлаждения * 293
- •Глава 12. Система воздухопитаип 324
- •Глава 13. Система выпуска 355
- •Глава 14. Система пуска двигателей 379
- •Глава 15. Принципы подбора двигателя внутреннего сгорания для транспортного средства 386
1’ис.
2.9. Размещение противовесов в кон
сгрукции четырехколенного плоского
ко иенчатого вала, обеспечивающее его
наи нучшую внутреннюю и внешнюю уравно
вешенность
Принцип
использования противовесов в
самоуравновешенных налах рассмотрен
на рис. 2.7 на примере плоского четырехколен-
иого вала.
Из
приведенной схемы следует, что силы К„
действующие на кривошипах, нагружают
опоры вала: 1-ю опору — силой 0,5АГГ;
3-ю
«шору
— силой К,;
5-ю опору — силой 0,5.ЙГ,.
Для
их разгрузки может быть использована
система противовесов, показанная
на рис. 2.8.
Здесь
при статическом моменте противовесов
MCIJsp=0,5mf,
'LKr=0
и ~LMr=0,
а силы, нагружающие опоры с 1-й по 5-ю,
равны нулю. Однако при этом момент от
пары сил Кг,
действующих на 1-м
и 2-м
кривошипах, Мл_2,
уравновешиваясь парой центробежных
сил 1-го
и 2-го
противовесов нагружает конструкцию
вала
изгибающими
напряжениями (все сказанное выше в
равной мере справедливо и для 3-го, и
4-го кривошипов).
Для
устранения данного недостатка в
некоторых двигателях применяется
система противовесов, приведенная на
рис. 2.9.
В
этом случае Кг
уравновешивается непосредственно на
кривошипе, что позволяет при полностью
уравновешенном вале (£ЛТг=0;
ЪМ,=0)
и полностью разгруженных опорах в
значительной мере разгрузить его
конструкцию от действия изгибающих
моментов. Однако при этом суммарный
статический момент противовесов
увеличивается в 2
раза.
Валы,
кривошипы которых расположены в
нескольких плоско- <• гях, носят
название пространственных.
Рассмотрим
принцип их уравновешивания на примере
трехко- иснного вала с кривошипами,
расположенными в трех плоскостях иод
углом £=120°. Схема его приведена на рис.
2.10, а.
392.3. Принципы уравнорешивания пространственных коленчатых валов
Рис.
2.10. К анализу уравновешенности
трехколенного пространственного
коленчатого вала с углом между
кривошипами 120°:
а
— схема нагружения; б
— векторная диаграмма центробежных
сил; в
— векторная диаграмма
момента
центробежных сил
Результирующая
центробежных сил в данном случае
определяется векторным суммированием
сил Л,, действующих на отдельных
кривошипах, и, как видно из рис. 2.10,
б, равна нулю:
ZKr=1)+К^2)+з)=0.
—» —¥ —*
Момент
этих сил относительно точки О:
ИМГ=.
Модули слагаемых моментов сил Кг,
действующих в плоскостях 1-го
и 3-го кривошипов, |М^1)|
= |М^з)]=А,а=/и^со2а.
Векторное суммирование этих моментов
представлено на рис. 2.10, в.
Отсюда следует, что модуль суммарного
момента, определенный по теореме
косинусов из заштрихованного
треугольника,
\ZM,\=у/(К4)2
+ сад2
- 2(ВД2
cos
120°
=
=у/ъ
К,а=у/Зт^со2а.
Угол
<ри
определяющий плоскость его действия
относительно плоскости 1-го кривошипа,
равен 30°. Уравновесить этот момент
40
Рис.
2.11. Размещение противовесов
к
трехколенном пространственном
ко-
ленчатом вале, обеспечивающее
его
полную внешнюю и наилучшую
внут-
реннюю уравновешенность
можно,
создав в плоскости его действия Л/№
= — ЕЛ/,; |Мур| = |ЕМ,| = К„РЬ=у[Ътггаз2а.
Для этого, как показано на рис. 2.10, а,
в плоскости действия ХМГ
на продолжении крайних щек устанавливаются
противовесы со статическим моментом
МСТмр=^/Зтгг(а1Ь).
Возникающая при этом на плече Ъ
пара сил К11р=МС1.прса2=тврр11ра)2
создает необходимый для уравновешивания
момент МуР.
Этот
вариант размещения противовесов
обеспечивает
полную уравновешенность вала при
минимальной суммарной материалоемкости
противовесов (ЕЛ/стпр->тт).
Однако при этом все коренные «•норы
нагружаются центробежными силами, а
конструкция вала — п и ибающими
моментами.
Радикальный
способ их разгрузки при сохранении
полной урав- моксшенности вала —
размещение противовесов на продолжении
■к ex
его
щек, как это показано на рис. 2.11,
но при этом максимально
возрастает
материалоемкость конструкции (ЕЛ/^щ,-*
max).
На
практике часто используются комбинации
этих двух схем, ■I
I
о позволяет частично разгрузить опоры
и конструкцию вала при промежуточном
значении Л/Ст.„р.
ПРИНЦИПЫ
УРАВНОВЕШИВАНИЯ СИЛ ИНЕРЦИИ МАСС,
ДВИЖУЩИХСЯ ВОЗВРАТНО-ПОСТУПАТЕЛЬНО
Идея
конструкции механизма
для уравновешивания сил инерции мерного
PjX
и
второго Р}п
порядков базируется на возможности
подставления их в виде геометрический
суммы вращающихся н противоположных
направлениях центробежных сил. На рис.
’ I 7,
а
сила Pji
представлена
как результат сложения вектора с молу
«см (0,5 С+),
вращающегося с угловой скоростью +£о,
и вектора (I!,')(’ ), имеющего угловую
частоту —
со.
Здесь же приведен меха- пи
iM
уравновешивания
силы Pfl,
состоящий
из противовесов со I
I
it
I
ическим моментом MCI_npi=mapipupl,
которые
размещены на двух
41
Рис.
2.12. Принцип уравновешивания сил инерции
масс, совершающих возвратнопоступательное
движение:
а
— первого порядка; б
— второго порядка
валах,
вращающихся с угловой частотой ±со.
Возникающие при этом центробежные силы
К^+
и вращаются синхронно
с
уравновешиваемыми ими силами 0,5С+
и 0,5С~. Условие уравновешивания Кщ,1==
0,5С=0,5/п, гсо2
выполняется при Л/СТПР1
= 0,5/и/.
На
рис. 2.12, б
показан аналогичный механизм
уравновешивания силы Pja-
Здесь
Р/а
— геометрическая сумма сил 0,5ЯС+
и 0,5АС , вращающихся соответственно с
угловыми скоростями +2со
и —2со.
Каждая из них уравновешивается
центробежными силами К^р2
и 42
Ktipl,
которые
образуются при вращении с угловыми
частотами +2со противовесов, имеющих
Мгл.тщ2=тШр2Рщ,2,
на двух дополнительных валах. Условие
уравновешивания Кпр2=тЦр2Рщ)2(2со)2
= 0,5АС= ~0,5Хт/со2
выполняется при МС1_ща=тпр2рВр2=11вЩг.
АНАЛИЗ
УРАВНОВЕШЕННОСТИ И УРАВНОВЕШИВАНИЕ
ДВИГАТЕЛЕЙ С ЛИНЕЙНЫМ РАСПОЛОЖЕНИЕМ
ЦИЛИНДРОВ
ОДНОЦИЛИНДРОВЫЙ
ДВИГАТЕЛЬ
Одноцилиндровый
двигатель имеет одноколенный вал,
уравно- исшивание которого рассмотрено
в разд. 2.3.
Уравновешивание
сил инерции Pfi
и
Р}ц
реализуется с помощью механизма
Ланчестера, построенного на базе
рассмотренных выше принципов их
уравновешивания.
Его
основу составляют (рис. 2.13):
43
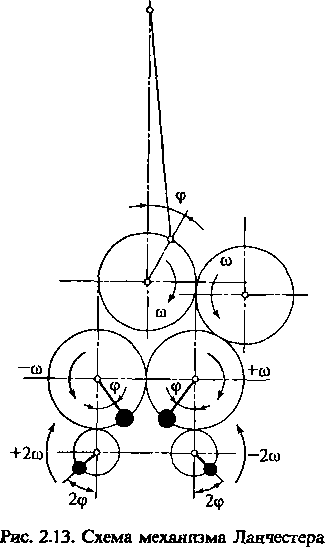
два
вала, вращающиеся с угловы-
ми
скоростями ±ш, и установленные
на
них противовесы со статическим
мо-
ментом MCT_npl
= 0,5mjr,
они
уравнове-
шивают силу инерции Рр,
два
вала, вращающиеся с угловы-
ми
частотами +2со,
и установленные
на них противовесы
со статическим мо-
ментом Л/СГ
Цр2=1/вА/Иуг;
они уравнове-
шивают силу инерции
Pjn.
Вследствие
громоздкости и конст-
руктивной
сложности механизм Ланче-
стера
практически не используется
в
транспортных двигателях и применя-
ется
лишь в специальных стационар-
ных
установках, предназначенных для
проведения
исследовательских работ.
В
большинстве транспортных и
промышленных
одноцилиндровых ДВС
для облегчения
работы упругих эле-
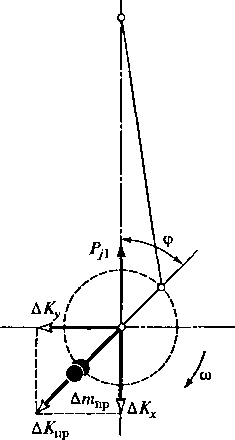
Рис.
2.14. Принцип переноса ча- менхов
подвески используется их разг-
сти
силы инерции первого по- J г
рядка
в плоскость, перпевдику- рузка
за счет переноса части силы Рд лярную
оси цилиндра в
плоскость, перпендикулярную оси ци
линдра.
Для
этого на противовесы вала устанавливается
дополнительная масса Д/л1ф,
как это показано на рис. 2.14. При вращении
кривошипа с угловой частотой со
возникает сила АК^—Ат^р^са2.
Ее проекция на ось цилиндра АКХ=AK^cos
ср.
Эта сила может уравновесить часть силы
Pj\
=
С
cos
ср.
Необходимые для этого конструктивные
параметры противовеса определяются
из равенства АКХ~
АР Здесь
Л = 0...1 — часть силы Рл,
подлежащая уравновешиванию. Отсюда
при Mcinp=Amjr
вдоль
оси цилиндра действует сила Pz=
=
РА
—АКХ=(1
— А)Рд.
Однако при этом в перпендикулярном
направлении возникает сила АКУ=АКщ,
sin
q>=М^
щСо2
sin
=Л
С sin
(р.
ДВУХЦИЛИНДРОВЫЕ
ДВИГАТЕЛИ
Двухцилиндровые
двигатели выполняются по двум
конструктивным схемам:
с
углом между кривошипами 180°—2Р («5 =
180°); с углом между кривошипами 360°—2Р
(5 = 360°)..
Двигатель
2Р (5 = 180°). Конструктивная схема и анализ
уравновешенности данного двигателя
приведены в разд. 2.1.2. Неуравновешенными
в двигателе являются:
44
суммарный
момент центробежных сил ХМг=т^ш2а\
суммарная
сила инерции 2-го порядка =2?.С
cos
2ср\
суммарный
момент сил инерции 1-го
порядка — ЕЛ/д= Cacoscp.
Уравновешивание
ИМ,
для плоского двухколенного вала,
используемого в 2Р (5= 180°), рассмотрено
в разд. 2.3.
Неуравновешенность
по ZP/n
сравнительно
невелика, и этот силовой фактор в
большинстве конструкций оставляют
неуравновешенным.
Наиболее
существенно на уравновешенность
двигателя из перечисленных силовых
факторов влияет суммарный момент сил
инер- иии 1-го порядка = Са
cos
(р.
Для его уравновешивания может
<)мгь
использован специальный механизм,
схема которого приведена на рис.
2.15, а.
Конструкция уравновешивающего механизма
н шачительной мере определяется тем
обстоятельством, что ХА/д не изменяет
плоскость своего действия; он всегда
находится в плоскости осей цилиндров,
как это показано на силовой схеме
механизма (рис. 2.15, б). Противовесы
на дополнительных валах (их угловые <
корости +со
и —со) создают на плече b
пары
сил, формирующие моменты:
.Л^ур——А/оуцрО
b
fn^pnpii)
Ъ,
=
К~Ь=М^саРЬ=т^рцОрЬ,
■к-к
горы которых перпендикулярны плоскостям
расположения про- шновесов. Проекции
этих моментов на оси х
и у
равны соответст-
I1CIIIIO
=
К^Ь
cos
ф;
м:
= куь
sin
q>;
М~
= K~b
cos ( - <p);
M~ = K^b
sin (-
q>).
Таким
образом M*
=M~
и
ЪМУ=2М„
вра)2Ь
cos
ф,
в то время как 1/.' =-М~
и1М,=0.
Условие
уравновешивания ЕЛ/,Т,
как это следует из силовой
чгмы,
'LMfl='LMy,
что
имеет место при MCTap
= 1f2mJr(a/b).
Конструкция
механизма может быть существенно
упрощена, п ни в качестве одного из
валов, а именно вала, вращающегося
у1ловой
скоростью +со,
использовать коленчатый вал (рис.
•'
I
s,
в).
Как
существенный недостаток двигателя 2Р
(5=180°) следует и I метить, что четырехтактные
ДВС при такой компоновке кривошипов
имеют неравномерное чередование рабочих
ходов соответст- ипию через 180 и 540°
поворота коленчатого вала.
45
Рис.
2.1 S.
Уравновешивание
двухцилиндрового рядного двигателя с
углом между
кривошипами
180°:
а
— принцип уравновешивания момента сил
инерции первого порядка; б
— векторная диаграмма формирования
уравновешивающего момента; в
— схема механизма уравновешивания
момента сил инерции первого порядка
с одним дополнительным валом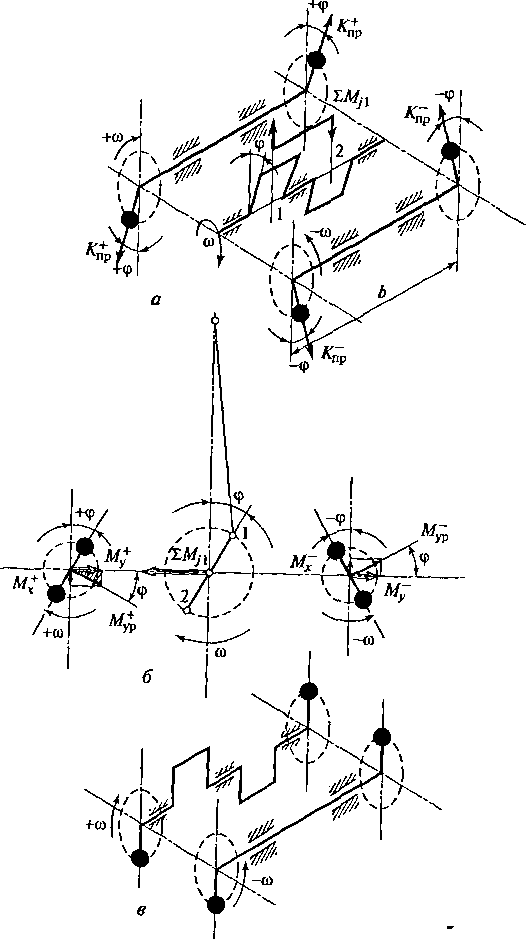
Двигатель
2Р (5 = 360°). Компоновочная схема двигателя
приведена на рис. 2.16, а.
Практическая целесообразность его в
значительной мере определяется
возможностью обеспечения равномерного
чередования рабочих ходов (через 360°
поворота коленчатого вала) в четырехтактных
ДВС.
По
уравновешенности данный двигатель
эквивалентен двигателю одноцилиндровому,
имеющему удвоенные массы подвижных
шементов. В соответствии с этим силовые
факторы, определяющие его уравновешенность:
ИРд=2Pji=2Ccos
<р;
ZPyn=2Рщ=2ХС
cos
2ср;
l,Kr=2Kr=2mrrco2-
2ЖЛ
= 0; Щ,-п= 0; 2Ж,=0.
На
рис. 2.16, б
приведена схема уравновешивания ЪМп
согласно которой на продолжении щек
размещаются противовесы со статическим
моментом Meinp=ll2mf.
Неуравновешенность,
вызываемая силой Zi/n,
относительно
не- пелика, и данный силовой фактор в
большинстве конструкций ДВС оставляют
неуравновешенным.
Обязательному
уравновешиванию в двигателях 2Р (5
= 360°) подвергается наиболее значимый
из неуравновешенных силовых фак-
оров
— hPfl=2Сcos
ср.
На практике эта задача может быть
решена двумя способами:
использованием
части механизма Ланчестера,
предназначенной для уравновешивания
силы инерции первого порядка, приняв
патический момент противовесов на
дополнительных валах, равным М„
npi=ntj
г;
применением
уравновешивающего механизма с двумя
дополнительными валами, вращающимися
в одном
направлении с угловой частотой
—со и дополнительными противовесами
на коленчатом пилу.
Схема
такого механизма приведена на рис.
2.16, в.
Здесь сила HPfl=2Pfl
замещена
эквивалентной ей геометрической суммой
двух сил с модулем С,
одна из которых (С+)
вращается с угловой скоростью + со
(синхронно с кривошипом), а другая (С-)
— с уг- иовой частотой —со.
Для
уравновешивания силы С+
масса противовесов на колен- ча I ом
валу увеличивается совокупно на величину
Ат^,
в результате ■кто возникает центробежная
сила К£р=Атпррщ,со2.
Условие уравновешивания Кщ
= С=т/гсо2
выполняется при Аотпр=»27г/р11р.
Сила
С~ уравновешивается равнодействующей
2K~V
двух
центробежных сил К^,
возникающих от вращения противовесов
на двух пополнительных валах, вращающихся
с угловой частотой —со
(синхронно с уравновешиваемой силой).
Оси вращения валов
47
Рис.
2.16. Уравновешивание двухцилиндрового
рядного двигателя с углом между
кривошипами
360°: ,
а
— схема двигателя; 6
— уравновешивание коленчатого вала;
в
— механизм уравновешивания суммарной
силы инерции первого порядка; г
— диаграммы моментов, уравновешиваемых
реакциями опор двигателя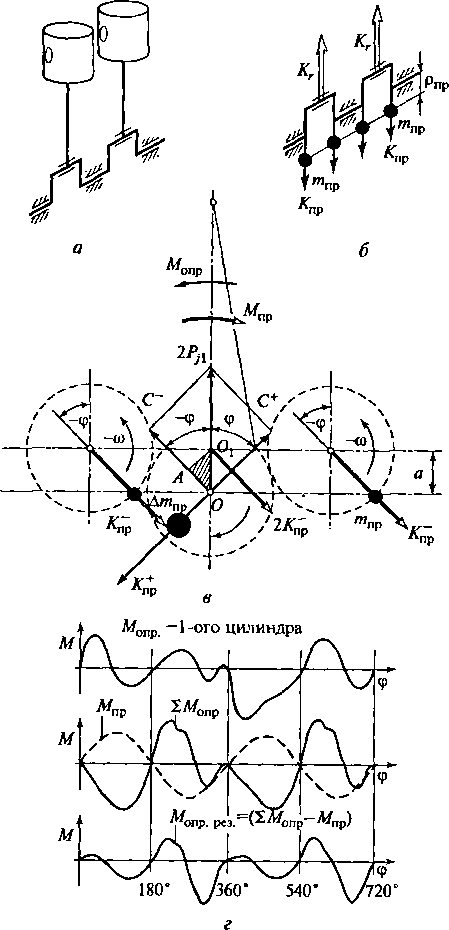
с
противовесами смещены относительно
оси коленчатого вала на неличину а
в направлении ВМТ.
Условие
уравновешивания 2K^p
= C=mjr(6l
выполняется
при
^ст-пр
' /
При
этом за счет смещения осей вращения
коленчатого вала и дополнительных
валов возникает момент —C(AOt)=Ca
sin
tp,
который
взаимодействует с Мопр,
как это показано на рис. 2.16, г.
И
результате результирующий момент
Мопр_ра=Мовр—Мвр,
передаваемый на опоры, имеет меньшую
неравномерность, чем момент опрокидывающий.
Это позволяет улучшить уравновешенность
дви- 1
ателя по опрокидывающему моменту.
Величина
смещения осей коленчатого и дополнительных
валов а
определяется
из условия обеспечения максимального
эффекта выра- пнивания Л/опр на наиболее
характерном эксплуатационном режиме
работы двигателя (обычно это режим
номинальной мощности). Учитывая то
обстоятельство, что Мопр(0
— периодическая функция с периодом
для четырехтактного двигателя Т—Лп/са,
он может быть разложен в ряд Фурье:
00
Monp(t)=Mcp+
£
Mksin(k(0t+<pk),
где
к=
1, 2, 3... it=-i
Так
как q>=(ot,
то
Л/щ,=Са
sin
(р
= Са
sin<y/
и
может нейтрализо- иать один из членов
тригонометрического полинома, а именно
член с к—
1. Это возможно при Mi
=
Са,
вследствие чего a—MJC.
ТРЕХЦИЛИНДРОВЫЙ
ДВИГАТЕЛЬ
Двигатель
имеет трехколенный пространственный
коленчатый нал, кривошипы которого
развернуты друг относительно друга на
Vi
ол
120°. Схема двигателя компоновки ЗР (5 =
120°) приведена на рис. 2.17, а.
К его достоинствам следует отнести
возможность иметь ранномерное чередование
рабочих ходов ка* в четырех-, так и в
циухтактном исполнении. ^
В
четырехтактном ДВС при порядке работы
цилиндров 1 — 2 — I - 1
рабочие ходы чередуются через 240°, в
двухтактном — через 120°
при работе цилиндров в порядке 1
— 3 — 2
— 1.
Анализ
уравновешенности и уравновешивание
коленчатого вала чнигателя ЗР (5= 120°)
рассмотрены ранее в разд. 2.3.
Суммарная
сила инерции первого порядка равна
нулю:
ХРц=Р,1(1)+Р,1(2)
+ Pji(3)
=
С
cos
q>
+
-+-
С cos
(tp
+120°)+С
cos(</>+240°)
= 0.
49
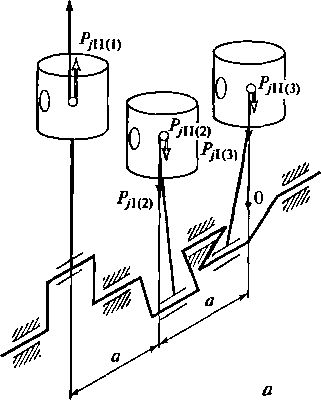
Рис.
2.17. Уравновешивание трехцилиндрового
рядного двигателя с углом между
кривошипами
120°:
а
— схема даигателя; б
— механизм уравновешивания момента
сил инерции первого порядка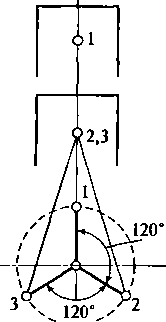

Суммарная
сила инерции второго порядка также
равна нулю:
VPjTi
=
РГП(1)
+ РЩ(2)
+ РЩ(3)
=
=AC
cos
2(р+ХС
cos
2((р
+120°)+AC
cos
2
(<р+240°)=0.
Суммарный
момент сил инерции первого порядка
неуравновешен; его значение
относительно точки О:
2Л/д(о)=Pjmy2.a+Pji(2)0=Са
[2
cos
срcos
(tp
+120°)]
=
=
Са
(1,5 cos
q>—0,866
sin <p).
Этот
момент действует всегда в плоскости
осей цилиндров
и уравновесить его можно, как и в случае
двигателя 2Р (5=180°), системой противовесов
на двух встречно вращающихся валах
(одним из них может являться коленчатый
вал). Схема такого механизма приведена
на рис. 2.17, б.
Для определения начального углово- ю
положения противовесов относительно
плоскости первого кривошипа найдем
экстремумы dLM^jdq
=
Са ( — 1,5 sin
—
0,866
cos
<р)=0,
откуда ИМ]1т„
= 1,732Са и имеет место при <р,= 150° и
ф2=330°.
Это означает, что при повороте 1-го
кривошипа па угол 150° противовесы на
обоих валах должны находиться в
плоскостях, параллельных плоскости
осей цилиндров,
как это показано на схеме, и создавать
там максимальный суммарный уравновешивающий
момент 1,МУР=(М£)+(М^Р).
Для этого противовесы должны
располагаться в плоскостях под углом
+ 30° к плоскости 1-го кривошипа. Их
статический момент определяется из
условия уравновешивания . Отсюда с
учетом того,
■I
го |М+| = IMypI=КщЬ=Мп.щ.Ьсо2;
Мстпр=0,866m,
г
(afb).
В
двигателе ЗР (5 = 120°) неуравновешен также
суммарный момент сил инерции второго
порядка:
ZAf,n(0)=Руп(1)2а+Р/щ$а=ХСа
[2
cos
2(р+cos
2
(<jо
+120°)] =
=
ХСа
(1,5 cos
2
ср+0,866
sin
2<р).
Он
также действует в плоскости осей
цилиндров и уравновесить по можно
установкой противовесов на двух
дополнительных ва- илх, вращающихся с
угловыми скоростями +2со. Ввиду
несущественности неуравновешивающего
действия ХМ,и и громоздкости механизма
уравновешивания его обычно оставляют
неуравновешенным.
51
2.5.4.
ЧЕТЫРЕХЦИЛИНДРОВЫЙ ДВИГАТЕЛЬ
Четырехтактный
четырехцилиндровый двигатель имеет
плоский четырехколенный коленчатый
вал с углами между кривошипами 180°,
что позволяет иметь равномерное
чередование рабочих ходов через 180°
при двух возможных порядках работы
цилиндров: I — 3 — 4 — 2—1 или 1—2 — 4 — 3
— 1.
Схема
двигателя с компоновкой 4Р (5= 180°)
приведена на рис. 2.18. Его коленчатый
вал удовлетворяет условиям самоуравнове-
шенности, поэтому суммарная сила инерции
масс, совершающих вращательное движение,
ХК„
так же как и момент этих сил ХЛ/„
автоматически равны нулю.
В
данном двигателе уравновешены и 2Л/л:
а=Р]%
1)
+ Pji(i)
+
Рда)+Рri(4)
=
=
Ceos
(р
+
С с os
(<р
+180°) + Ceos
(<р
+180е)+Ceos
q>=0;
£Л(г1(о)=Pji(i)’
1 >5а+Рд(2)'
0,5а+Р,i(3)
‘
0,5а+Р^'
1,5а=0.
Суммарная
же сила инерции второго порядка здесь
не уравновешена:
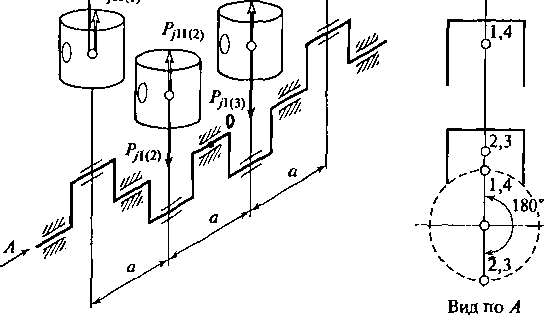
Рис.
2.18. К анализу уравновешенности
четырехцилиндрового рядного двигателя
с плоским коленчатым валом
pjm
рпт
Рfilm
ртп
52![]()
ZPj-П
— + P]1\(l)
+
РДО)
+ РД1(4)
—
=ХС
cos
2
ср+XCcos
2(ср
+180°)+ХС
cos
2
(ср
+180°)+ХС
cos
2ср
=
=4iCcos
2<р.
Однако
в силу симметричности коленчатого вала
суммарный момент этих сил уравновешен:
ЕЛ^/п(о)=Pju{v>'
lj5fl+-P/n(2)
'0,5a+Py-n(3)'0,5o-|-Pyli(4)'
l,5a=0.
Таким
образом, в двигателе 4Р (д=
180°) неуравновешен только один силовой
фактор ХР]Ъ—АХС
2
cos
ср.
Так
как по уравновешенности ЪР1П
четырехцилиндровый двига- 1сль
подобен одноцилиндровому при /и/Эи=4/и/,
то и уравновесить сю возможно той частью
механизма Ланчестера, которая
предназначена для уравновешивания
силы Руц,
т. е. двумя вращающимися с угловой
частотой ±2со
валами с установленными на них проти-
новесами со статическим моментом
МС1.вр=4(1/впугХ).
АНАЛИЗ
УРАВНОВЕШЕННОСТИ И УРАВНОВЕШИВАНИЕ
ДВИГАТЕЛЯ 5Р (<5=72°)
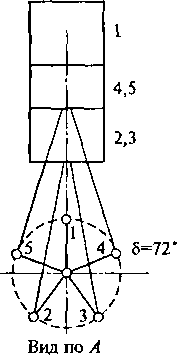
Схема
двигателя приведена на рис. 2.19, а. Он
имеет пятиколен- нмй вал с углом между
кривошипами 3=12°;
схема вала показана на рис. 2.19, б.
Такой вал обеспечивает равномерное в
четырехтактном варианте чередование
рабочих ходов с угловым интервалом <■)
= 720°// = 144° при порядке работы цилиндров
1 — 2 — 4 — 5 — » -1.
Рассмотрим
уравновешенность коленчатого вала по
центробежным силам инерции.
Как
следует из силовой схемы (рис. 2.20, а)
и многоугольника гил ЛТ,(.) (рис. 2.20,
б),
суммарная сила инерции
К*,=кг(1)+КГ(2)+К,(з)++Kr(j)=0.
i-1
л
Для
анализа момента центробежных сил
инерции Мг^
рассмотрим сумму этих моментов
относительно точки О
на рис. 2.20, а:
X
М,(0
— + МГ(5)]
+ [МГ(2)
+ МГ(4)].
1-1
53
^I(S)
Рис.
2.19.
Компоновочная
схема пятицилиндрового рядного двигателя
Модули
моментов попарно равны:
|Mr(1)|
=
IHffll
=К
• 2а=тггсо2
• 2а;
|Мг(2)|=|Mr(4)|=Kra=тггсо2а.
Векторы
моментов MrW
направлены
перпендикулярно плоскостям их
действия (плоскостям соответствующих
*-х кривошипов), как это показано на рис.
2.21,
а.
После
сложения векторов моментов М,(и
и М,(5)
(рис. 2.21, б)
получим,
что модуль суммарного момента
=
у/2М2т—2М2т
cos
72°
= 1,17557А/, (ц=2,35mrrco2a
и
вектор его направлен под углом 54° к
плоскости, перпендикулярной 1-му
кривошипу (рис. 2.21,
б).
Аналогично,
как показано на рис. 2.21, в,
модуль суммарного момента
|Мг(2,4)|=у/2М22)—2М2(1)
cos
144°
= 1,902msa>2a;
его
линия действия находится под углом 54°
к плоскости, перпендикулярной
плоскости 1-го
кривошипа.
54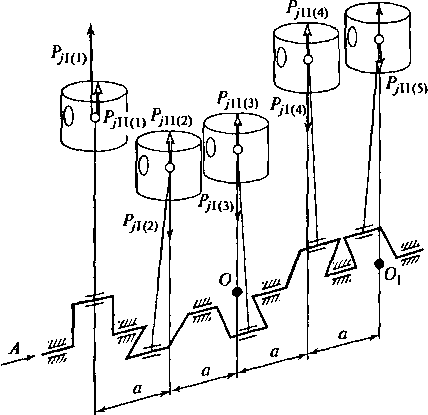
*r(5)
KrV)
6
Рис.
2.20.
Схема
нагружения коленчатого вала центробежными
силами инерции: а
— силовая схема; б — силовой многоугольник
Таким
образом, векторы М,(1>5)
и Мл(2,4)
имеют единую линию действия; суммарный
момент
£м,(
(0
=
|М,<1,5)1
- |МГ(2>4)|=0,449т^са2а
и
вектор его находится под углом 54° к
плоскости, перпендикулярной 1-му
кривошипу (рис. 2.21, г
и д).
Как следует из механики, сам момент
действует в плоскости, перпендикулярной
его вектору (см. рис. 2.21, д),
т. е. в плоскости под углом 54° к оси 1-го
кривошипа. Он может быть уравновешен
моментом Myv=Kupb,
создаваемым
парой центробежных сил Кщ,=тщ,рщ,(ог
противовесов, расположение на крайних
щеках вала в плоскости действия момента.
s
Условие
уравновешивания: |Мур| =
Ем,
г(0
Отсюда
может быть
определен
необходимый для этого статический
момент противовесов Л/стлр=/ИдрРпр=0,449mrr
(а/Ь).
Рассмотрим
далее уравновешенность двигателя по
силам инерции масс, движущихся
возвратно-поступательно, и по моментам
» I их сил:
55![]()
i,5) а Плоскость
Рис.
2.21. Диаграмма формирования суммарного
момента центробежных сил
инерции:
а
— векторная диаграмма моментов,
действующих на отдельных кривошипах;
6
— векторная диаграмма суммарного
момента на 1-м и S-м
кривошипах; в
— векторная диаграмма суммарного
момента на 2-м и 4-м кривошипах; г
— векторная диаграмма суммарного
момента всех центробежных сил вала; д
— схема формирования уравновешивающего
момента
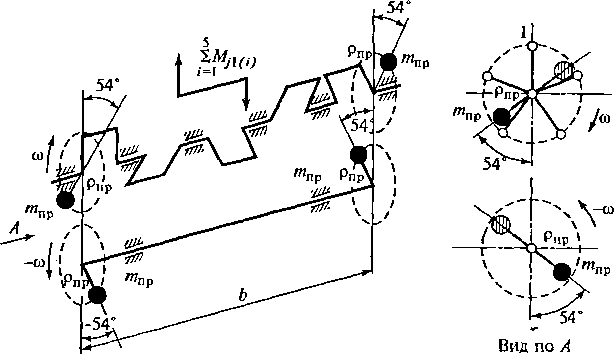
Рис.
2.22. Конструктивная схема механизма
уравновешивания суммарного момента
сил инерции первого порядка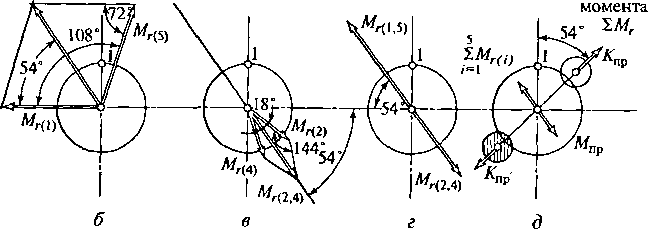
5
P,щ
=
PjHI)
+ P,1(2)
+ PД(3)
+
P,1(4)
+ P,1(5)
= С
[cos
ф
+
cos
(</>
+
216°)
+
1
+
cos (<p
+144°)+cos (<p
+ 72°)+cos (q>
4-288°)] = 0;
5
P/11(0
~
P/Щ1)
+
-P/11(2)
+
PДО)
+
PfU(4)
+
P/U(5)
=
AC [cos 2(p
+ /-1
+
cos 2 (ф+216°)
+ cos 2(<p+144°) + cos 2(<p + 72°)+cos 2(<p + 288°)] =
-0;
суммарный
момент сил инерции первого порядка
относительно точки О,:
5
X
Л/д(0
=
Л^/1(1)
+ Л(д(2)
+ ^/,1(3) + Л/,1(4) + Л/д(5) =
/=■
1
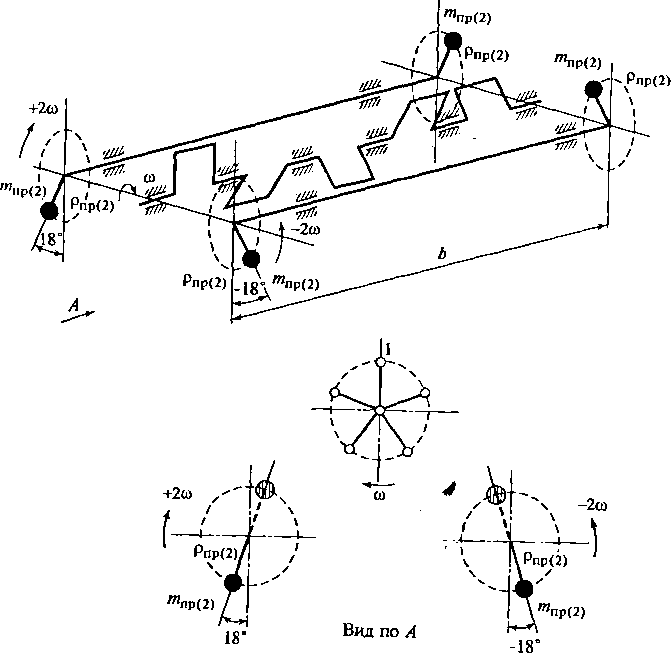
1'ис.
2.23. Конструктивная схема механизма
уравновешивания суммарного момента
сил инерции второго порядка
57
—4c//i(i)+ЗлР/1(2)+2а/ук3)+а/д(4)+0—4аС
cos
<р+
+
ЗаС cos
(<р+216°)
+ 2 аС
cos
(<р
+144°)+аС
cos
(<р
+ 72е)+0=
=аС(0,2639
cos
<р—0,36327
sin
ср)
= 0,449аС cos
(<р
+ 54°).
Этот
момент действует в плоскости осей
цилиндров и имеет экстремальные значения
+0,449аС при <9=306° и <р
=
126°.
Схема
механизма его уравновешивания приведена
на рис. 2.22. Статический момент противовесов
на продолжении крайних щек коленчатого
вала и на дополнительном валу Мпрсг=
=0,2245С(а/6)/ш2
= 0,2245/и, г (а/Ь);
4)
суммарный момент сил инерции второго
порядка относительно точки О,:
S
X
Мщя=А/,-п(1)+Л/щР)+Л/д1(з)+Mjnffi+Л/уп(5)=
1-1
=4аРу11(1)+3a/yn(2)+2аРдцц++0=
=4aACcos
2ф+ЪаХС
cos
2(<р
+ 216°)+2 аХС
cos
2
(q>
+144°)+
+аЛС
cos
2
(<tp+72°)+0=аХС
[4,736 cos
2<р—1,5388
sin
2<р\=
=4,9797аЛС
cos
(2q>
+18°).
Этот
момент всегда действует в плоскости
осей цилиндров и имеет экстремальные
значения ±4,9797eAC
при
<9=81, 171, 261 и 351°.
Принципиально
его можно уравновесить системой двух
валов с противовесами, вращающимися с
угловыми частотами ±2со
(рис.
. Статический
момент противовесов на дополнительных,
вращающихся навстречу друг другу
валах
Л/пр-стф=2,48985ЛС
(а/6)/4со2
= 0,6224625Ат/ (а/Ь).
ШЕСТИЦИЛИНДРОВЫЙ
ДВИГАТЕЛЬ
Шестицилиндровый
четырехтактный линейный
двигатель (рис.
имеет
пространственный шестиколенный вал
с углом между кривошипами 120°,
что обеспечивает равномерное чередование
рабочих ходов с угловым интервалом
120°
при четырех возможных порядках работы.
Наиболее востребованными из них
являются: 1 — 5 — 3 — 6
— 2 — 4 — 1; 1 — 4 — 2 — 6
— 3 — 5 — 1.
Коленчатый
вал самоуравновешен и ЕК,=0; ЕМ,=0.
Сипы
инерции первого и второго порядков,
так же как и центробежные силы,
уравновешены и не создают неуравновешенных
моментов:
S8
ЕР/1
=
Р/1(1)
+ Р,1(2)
+ Ру1(3) + Р,1(4) +
P/1(5)
+
Pm
=
=
Ceos
<p+C
cos
(9+240°)
+ Ceos
(cp
+120°) + С
cos
(<p+120°)
+
+
С
cos
(q>+240°)
+ С
cos
(p=0;
EPja
= P/П(1)
+
PjTM.2)
+ PДО)
+
P/П(4)
+
P/11(5)
+
PyII(6)
=
=
AC cos 2xp
+ AC cos 2(<p+240°)+AC
cos 2{tp
+120°)
+
+AC
cos 2(ф+240°)
+ AC cos 2(<p
+120°)+AC' 2 cos q>=0;
ЕЛ/да=P/i(i)'
2,5a+P/i(2)' 1,5a+Pд(3)'
0,5a+Pда'
0,5a+
+
P/1(5)'
1,5a+P/од'
2,5a=0;
£Л//що)=Pjii(i)
‘ 2,5a+P/11(2)'
1,5a+Р/щз)'
0,5a +
+P/п(4)'
0,5a+P/п(5)'
1,5a+P/п(в)'
2,5a=0.
Таким
образом, двигатель 6P
(S=
120°) полностью
уравновешен по силам инерции и моментам
этих сил.

АНАЛИЗ
УРАВНОВЕШЕННОСТИ И УРАВНОВЕШИВАНИЕ
У-ОБРАЗНЫХ ДВИГАТЕЛЕЙ
При
анализе уравновешенности V-образных
двигателей их рассматривают как
совокупность //2
(/ — количество цилиндров) двухцилиндровых
V-образных
двигателей с тем же углом развала осей
цилиндров у. Их кривошипы повернуты
друг относительно друга на угол 8,
определяемый компоновочной схемой
двигателя, и вращаются синхронно.
Одноименные
силовые факторы на отдельных условных
двухцилиндровых двигателях далее
суммируются по длине коленчатого вала.
Таким
образом, анализу уравновешенности
V-образного
двигателя предшествует анализ
уравновешенности двухцилиндрового V-
образного двигателя с тем же углом
развала осей цилиндров у.
В
автотракторной технике наибольшее
распространение получили V-образные
двигатели с у=90°.
АНАЛИЗ
УРАВНОВЕШЕННОСТИ ДВУХЦИЛИНДРОВОГО
V-ОБРАЗНОГО
ДВИГАТЕЛЯ С УГЛОМ РАЗВАЛА 90°-2V
(у=90°)
Двигатель
2V
(у=90е),
схема которого представлена на рис.
2.25, а,
имеет одноколенный вал. Для его
уравновешивания (рис. 2.25, б)
на
продолжении щек устанавливаются два
противовеса с Л/сг
пр=
—MurPvp
=
11гтг'г->
где тгг=т1+2тшл.
Здесь удвоение массы шатуна, приведенной
к кривошипу т^,
связано с тем, что в 2V
(у=90°)
на кривошип опираются два
шатуна. В соответствии с этим центробежная
сила инерции Кг'=тг'г<о2.
Суммарная
сила инерции первого порядка формируется
как геометрическая сумма одноименных
сил левого (индекс — л) и правого
(индекс — п) цилиндров:
ЕРл=Рад+Р/i(n)i
|Рд(л)1
= С cos
ф;
|Рyi(n)|=С
cos
(<р
+ 270°)=С sin
(р.
Модуль
суммарной силы
№1=y/Pfl(a)+Pfl(n)=у/(С
cos
ф)2+(С
sin
ф)2
= С=const.
Угол
между вектором ХРЛ
и осью левого цилиндра:
а=arctg
[Рд(П)/Рд(л)]=(р
-
Таким
образом, в двигателе 2V
(у=90°)
суммарная сила инерции первого порядка
ZP7l=C=const
и
направлена по кривошипу от
60
Рис.
2.25. К анализу уравновешенности
двухцилиндрового V-образного
двигателя с углом развала осей цилиндров
90°:
к
силовая схема; 6
— уравновешивание суммарной силы
инерции первого порядха; в
— эквивалентная силовая схема
центра
его вращения (аналогичными свойствами
обладает центробежная сила К’г).
Соответственно она может быть
уравновешена установкой на противовесах
дополнительных масс Атщ>=
Суммарная
сила инерции второго порядка:
ЕР,11
= Р/П(л)
+ PjH(n),
IPД(л)|
=AC
cos
2(р\
|Р/щп)|=АС
cos
2(<р
+
270°) = — AC
cos
2<р;
|2Р/п|
= -yjPfll(n)
+
PflKjl)
=
=-y/^ACcos^p+XACcos^)2
=
AC cos
2ф.
Угол
между осью левого цилиндра и вектором
ЕР/п равен <pi—
arctg[(Рда(П)/Р/п(л)]=arctg
[—1]=45
или 135°.
61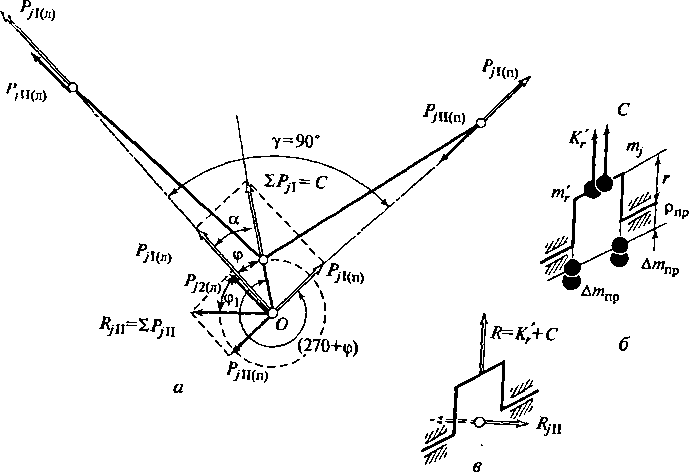
Таким
образом, при анализе уравновешенности
V-образного
многоцилиндрового двигателя с у=90°
каждый условный двухцилиндровый
двигатель, состоящий из кривошипа и
одноименных цилиндров
правого и левого рядов, заменяется
кривошипом с приложенными к нему
следующими силами (рис. 2.25, в):
R=Kr'+C=
=(mr'+nij)ra)2,
направленной
по его оси от центра вращения; 'ZRja=
=y/21Ccos2(p,
направленной
перпендикулярно плоскости осей
цилиндров.
ШЕСТИЦИЛИНДРОВЫЙ
ДВИГАТЕЛЬ С УГЛОМ РАЗВАЛА 90° И УГЛОМ
МЕЖДУ КРИВОШИПАМИ 120°-6V
(у=90°)
Двигатель
6V
(у
= 90°) (рис. 2.26) имеет неравномерное
чередование рабочих ходов (90—150°)
при порядке работы цилиндров 1л
— 1П
— 2Л
— 2п — Зл
— 3„ — 1. Для анализа уравновешенности
он может быть рассмотрен как
совокупность трех двигателей 2V
(у=90°),
кривошипы которых развернуты на угол
120°. К каждому кривошипу приложены
силы:
R<i)=R{2)—R(i)=Kr-\rC=(m'r+т^г(й2\
=\J2
ХС
cos
2(pt
£./?ущ2)—у/2
ХСcos
2(ср
"Ь120°),
YRnm=у/2
ХС
cos
2(ip
+
240°).
Оценка
уравновешенности данной схемы по силам
Л и по их моментам методически аналогична
анализу уравновешенности
Рис.
2.26. Анализ уравновешенности
шестицилиндрового V-образного
двигателя с углом развала осей цилиндров
90°:
а
— схема двигателя; б
— схема нагружения коленчатого вала
силами Л
и Луц
62
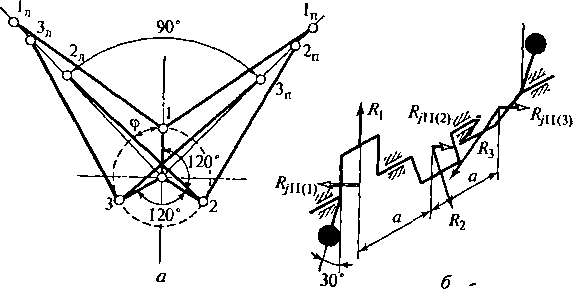
рехколенного
вала с 5=120° (см. разд. 2.3) с той лишь
разницей, чго здесь вместо сил К,
фигурируют силы R.
Вследствие
этого
2
£R=0.
Так
как R=Kr+C=K’r+Y1J>jь
то одновременно выполняют-
б
6
см
два условия уравновешенности: £К,=0и£Рл=0.
Момент
сил R
равен
|Е Мл|=у/b
Ra—у/ъ
(т'г+т^гт2а.
Он действует под углом 30° к плоскости
первого кривошипа и может быть уравновешен
двумя противовесами, установленными
на продолжении крайних щек под углом
30° к плоскости его действия. Для этого
статический
момент = у/з(т’г+т^г(а/b).
При
этом одновре-
мснно
решается проблема уравновешивания,
2)Мл=0 и £МЛ=0.
Двигатель
6V
(у=90°)
уравновешен по силам инерции второго
порядка, так как
2
2
2
Z=Z +Л
РМЯ+Е
^>П(3)=
=yfl
кС
[cos
2хр+cos
2(q>
+120°)+cos
2(ср
+ 240°)]=0.
Неуравновешенным
является суммарный момент этих сил:
ЪМщ=Rj-щ
1)2д+=[cos
2
ср+cos
2
{(р
+120°)J
=
=
y/lkCa
[1,5
cos
2<р+0,866
sin
2<р]
ф
0.
Он
действует в горизонтальной плоскости
и имеет максимум ZMjnmsx=
\,пъгф.1Са
при ф=15 и 195°. Этот момент может быть
уравновешен противовесами, установленными
на двух вращающихся в противоположных
направлениях с угловыми скоростями
2со
дополнительных
валах. Противовесы располагаются так,
чтобы при <Р
=
15, 105, 195 и 285° их центробежные силы
действовали в гори- юнтальной плоскости
(в плоскости действия ZA/,n)
и
создавали максимальный уравновешивающий
момент.
Вследствие
конструктивной сложности в практических
конструкциях ДВС такой механизм не
применяется.
ВОСЬМИЦИЛИНДРОВЫЙ
ДВИГАТЕЛЬ С УГЛОМ РАЗВАЛА 90°—8V
(у=90°)
Двигатель
8V
(у=90°)
в большинстве конструкций имеет
крестообразный коленчатый вал (рис.
2.27, а),
что при наиболее распространенном
порядке работы 1л
— 1п
— 4Л
— 4П
— 2„ — Зл
—
63
Рис.
2.27. Уравновешивааие восьмицилиндрового
V-образного
двигателя с углом развала 90° и
крестообразным коленчатым валом:
а
— саповая схема; 6
— векторная диаграмма сил Л; в
— векторная диаграмма моментов ш R
Зп
— 2л
— 1л
обеспечивает равномерное через 90°
чередование рабочих ходов.
При
анализе уравновешенности такой двигатель
может быть представлен как совокупность
четырех двигателей 2V
(у=90°),
кривошипы которых расположены в двух
плоскостях, находящихся под углом
90°. На каждом из них действуют силы i^,
4)
и
^
-¥
-* -*■ 2Лдц1.„4).
Как следует из рис. 2.27, б, £ R=
R(l)+R(2)+R(3)+R(4)=0.
Момент
этих сил 2,M*=Mw_4)+MJ!(2-3).
Здесь
|МЛ(1_4)|=Л'
За= 1
64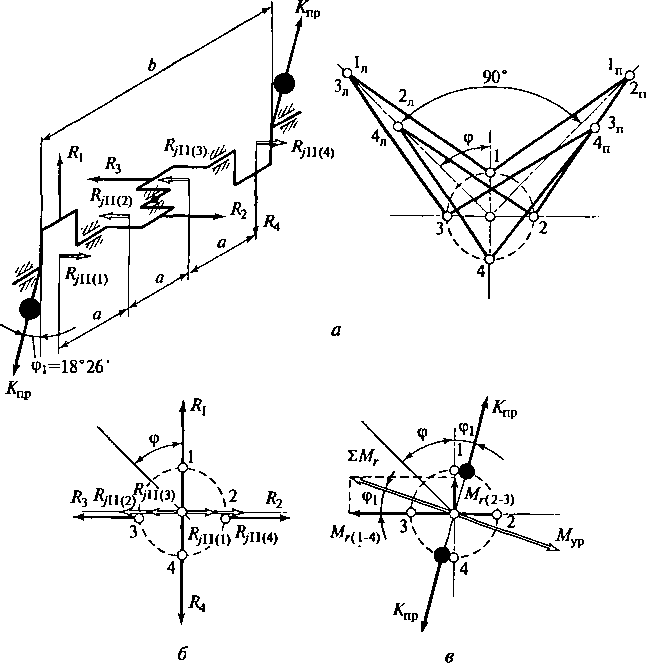
=
(т'г+т})г(о2За
—г
момент сил /fy)
и
i^4),
действующий
в плоскости 1-го и 4-го кривошипов (вектор
его перпендикулярен данной плоскости,
см. рис. 2.27, в); |МЛр_3)|=Ла=(т'+/я>)гш2а
— момент сил Л(2)
и ^3),
действующий в плоскости 2-го и 3-го
кривошипов. Модуль суммарного момента
сил R
ем*.
=у/м2ц(1
_4)+М2щ2-з)=V
ЮЛа=-y/lO
(т'+т])гсо2а.
Угол
между вектором £МЛ
и плоскостью 2-го и 3-го кривопшпов
<р,=arctg
[Л/Л(2_3)/Л/Л(1_4)]=arctg
[1/3]
= 18°26'.
8
Таким
образом, плоскость действия момента
расположена
под
углом 18°26' к плоскости 1-го
кривошипа.
Для
его уравновешивания в этой плоскости
на продолжении крайних щек располагаются
два противовеса, центробежные силы
которых Кщ
создают на плече b
уравновешивающий
момент М„=
= КпрЬ=МС1_Щ)со2Ь.
8
Условие
уравновешивания: £ Мя=Mw,
откуда
MmJ9—-v/10
(m'r+mj)r
(ajb).
Суммарная
сила инерции второго порядка -I-
Х7?уп(3)+Л,ц(4).
Все эти силы действуют в поперечной
плоскости, имеют параллельные линии
действия и по величине равны:
£Л,щ1)=*J2XC
cos
2
(р\
=\/2
ХС
cos
2
(tp
+
90°) —— — -у/2 ХС
cos
2
(р\
ЕЛщ(3)=y/l
ХС
cos
2
(<р+270°)
= — у/2
ХС
cos
2
<р;
=лД
ХС
cos
2(tp
-f“
180°)=
у/2.
ХС
cos
2лрш
8
Отсюда
следует, что £ PJU=0.
Суммарный
момент сил инерции второго Порядка
относительно
8
тчки
О
(рис. 2.27, б) равен нулю: £A/J(1I(0)=0.
65
ШЕСТИЦИЛИНДРОВЫЙ
ДВИГАТЕЛЬ С УГЛОМ РАЗВАЛА 120°-6V
(у=120°)
Двигатель
6V
(у
= 120°) при использовании в его конструкции
трехколенного пространственного вала
с углом между кривошипами <5 = 120°
имеет равномерное чередование рабочих
ходов при порядке работы цилиндров 1л
— 1п
— 2Л
— 2„
— Зл
— Зп
— 1л.
Для
анализа уравновешенности этот двигатель
целесообразно рассматривать как
совокупность двух трехцилиндровых
однорядных ДВС, плоскости осей
цилиндров которых расположены под
з з
углом
120° (рис. 2.28). Так как сумма сил инерции
Y*Pfl
и
Х-^/п в
каждом
из условных трехцилиндровых двигателей
равна нулю, то
6
и
в двигателе 6V
(у
= 120е)
имеем: £Pji=0
и £Р/п=0.
В
каждом из условных трехцилиндровых
ДВС действует неуравновешенный
момент сил инерции первого порядка: з
X
^/<Кл)= Со (1,5 cos
(р—0,866
sin
ф)
— в плоскости осей цилиндров левого
ряда; з
£
Мт=Са
[1,5 cos
(<р+240°)
— 0,866 sin
(ср+240°)]
— в плоскости осей цилиндров правого
ряда.
6
^ 3
^ 3
- Для 6V
(у=
120°) Хмл=£М/цл)+ЕМд(ц)
и,
как это следует из схемы рис. 2.28, б,
X
М/ij——
2
£ Л/д(л) X cos
60°
J
.
Этот
момент в процессе работы двигателя
меняет свое значение, направление и
плоскость действия.
Обычно,
будучи неуравновешенным, он оказывает
большое возбуждающее воздействие
на опоры двигателя.
Принцип
функционирования механизма для
уравновешивания суммарного момента
сил инерции 1-го
порядка в двигателе 6V
(у
=
з
=
120°)
заключается в следующем. Для уравновешивания
^М,1(л)
необходимо,
как и для любого ЗР (5 = 120°), расположить
два противовеса с Л/ст
пр=0,866
т^г(а/Ь)
на коленчатом валу в плоскости под
углом +30° к первому кривошипу, а также
на дополнительном валу, вращающемся с
частотой —со
под углом —30°, как показа- 66
1'ис.
2.28. Уравновешивание шестицилиндрового
V-образного
двигателя с углом
развала
120°:
к
схема двигателя; б—
векторная диаграмма моментов сил
инерции первого порядка; « г
схемы механизмов уравновешивания
моментов сил инерции первого порядка
ооответст- чгашо левого и правого
условных трехцилиндровых рядных
двигателей; д
— схема уравновешивающего механизма;
е
— эквивалентная схема замещения системы
противовесов на дополнительном валу
но
на рис. 2.28, в.
Аналогичный механизм для уравновешивания
I
М,ад
приведен на рис. 2.28, г.
Противовесы
на коленчатом и дополнительном валах
могут (нить объединены, как это показано
на рис. 2.28, д.
На коленчатом пли у противовесы
совмещаются и могут быть заменены парой
67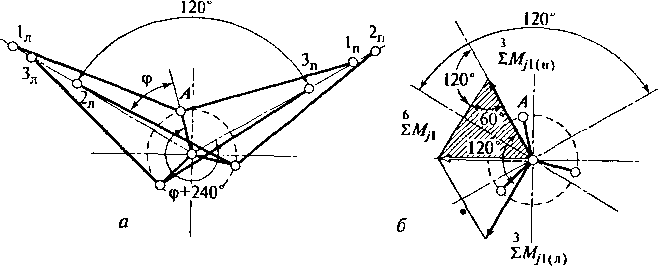

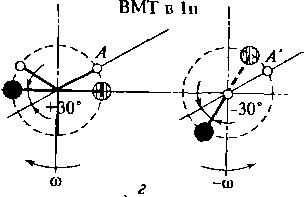

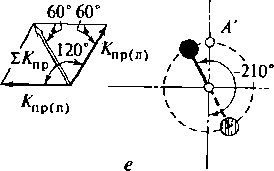
Рис.
2.29. Механизм уравновешивания суммарного
момента сил инерции первого порядка в
шестицилиндровом V-образном
двигателе с углом развала 120°
противовесов
с M^np=l,732ntjr(a/b),
расположенной
в плоскости под углом 30° к 1-му кривошипу.
На
дополнительном валу противовесы
располагаются в разных плоскостях,
находящихся под углом 120°. Они могут
быть заменены нарой противовесов,
размещенных в плоскости биссектрисы
угла
—► —* —»
120°,
при условии (рис. 2.28, е)
ЕКщ,=Кщ^)+Кщ^.
Таким
образом, IZKJ
=
IK^I
+
|Кцр.)п)|, откуда =0,866/и/
(а/Ь),
а
сами противовесы располагаются в
плоскости под углом —210°
к плоскости 1-го кривошипа. Кинематическая
схема уравновешивающего механизма
приведена на рис. 2.29.
В
двигателе 6V
(у
=120°) так же неуравновешен момент сил
инерции второго порядка. Его параметры
могут быть определены по методике,
аналогичной той, что использовалась
для анализа момента сил инерции первого
порядка.
Для
его уравновешивания понадобился бы
механизм, состоящий из двух
встречно-вращающихся с угловой частотой
±2со
валов и системой размещенных на них
противовесов.
Учитывая
сравнительно несущественное влияние
момента сил инерции второго порядка
на общую уравновешенность двигателя,
сложность и громоздкость механизма
уравновешивания, в большинстве
конструкций его оставляют неуравновешенным.
68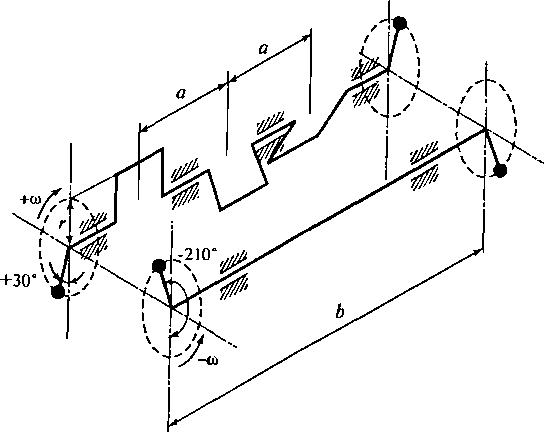
АНАЛИЗ
УРАВНОВЕШЕННОСТИ И УРАВНОВЕШИВАНИЕ
ДВИГАТЕЛЯ 10V
(у
= 144°)
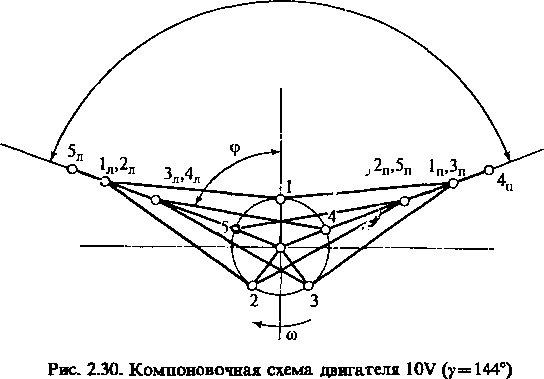
Схема
двигателя в положении, соответствующем
повороту первого кривошипа относительно
ВМТ в первом левом (1д) цилиндре на угол
<р,
приведена на рис. 2.30. Двигатель имеет
пятиколенный вал с углом между кривошипами
6
= 12°,
что обеспечивает равномерное в
четырехтактном варианте чередование
рабочих ходов с угловым интервалом
0=720%=72° при порядке работы цилиндров 1л
— 4П
— 2Л
— 5П
— 4Л
— Зп
— 5Л
— 1„ — Зл
— 2„
— 1л.
Силовые
факторы, ответственные за неуравновешенность
двигателя 10V
(у
= 144°), могут быть определены как
геометрическая сумма одноименных сил
и моментов, действующих на отдельных
(правом и левом) пятицилиндровых рядных
двигателях:
10-»
5
- 5
5
5
о
№=Х!Звд+№<п)=0>так
как
X
Р>п=X
Чвд+X руп(п)=о,
так
как Хр№)=ХЧткп)=0;
10 5 5
3)
Модуль
вектора суммарного момента сил инерции
первого порядка левого условного
пятицилиндрового двигателя
у=144"
69
Emj
‘/loo
=0,449aC
cos (<p
+ 54°).
Момент
действует в плоскости осей его цилиндров
и вектор направлен перпендикулярно
этой плоскости, как показано на рис.
2.31.
Аналогично,
для правого двигателя:
Ем,
УВД
=0,449аС
cos(<p+216°
+ 54°)=0,449aCcos
(q>+270°).
Модуль
суммарного момента может быть определен
по теореме косинусов из заштрихованного
силового треугольника (см. рис. 2.31):
ю
I Г/ 5 \2 /
5 \2 5 s "|1/2
+(5>/вд)
-2£Л/л(л)£Л/л(л)со8144^
=
=0,449аС
[cos2
(q>
+
54°)+cos2
(<р
-I-270°)—2
cos
(cp
+
54°) x x cos (q>+270°)
cos 144°]1/2.
10
Направление
вектора момента определяется углом Pi
—
=
90°+ai,
где
—угол между вектором момента и плоскостью
осей цилиндров левого ряда;
ОС]
= arcsin sin 144°|'.
Синтез
уравновешивающего механизма реализуется
как совокупность механизмов
уравновешивания моментов сил инерции
первого порядка левого (рис. 2.32, а)
и правого (рис. 2.32, б) условных
пятицилиндровых двигателей. Эти
механизмы представляют собой системы
противовесов со статическим моментом
Л^пр ст=0,2245/и/ (а/b),
расположенных
на продолжении крайних щек коленчатого
вала и на дополнительных ветре
чно-вращающихея валах под углами к
плоскости первого кривошипа соответственно
+ 54° и —54°. Совмещение этих двух
механизмов, выполненное на рис. 2.32, в,
показывает, что эффект полного
уравновешивания суммарного момента
сил инерции первого порядка может быть
достигнут следующей системой:
70
у=
144°
Рис.
2.31.
Схема
формирования суммарного момента сил
инерции первого порядка
двумя
противовесами со статическим моментом
^=2Л/Ст
пр=
= 0,449/и, г
(а/b),
располагаемыми
на концах коленчатого вала п плоскости
под углом + 54° к плоскости первого
кривошипа;
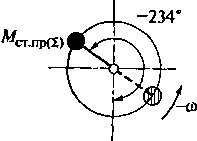
двумя
противовесами на концах дополнительного
вала, вращающегося с угловой частотой
—
to,
которые
расположены в плоскости под углом
—234° к первому кривошипу; их статический
момент может быть определен по теореме
косинусов из силового треугольника
центробежных сил противовесов,
размещаемых на дополнительном валу
(рис. 2.32, в):
Малрт=4/2^.op-2M2.npcos
108°=0,363/йуГ
(а/Ь).
Конструктивная
схема механизма
приведена на рис. 2.33.
Неуравновешенный
суммарный момеьг сил инерции второго
порядка
10
-* 5
_ 5
Yj
Мп=X
Мп(л)+X Щъ(и)
^ 0.
Модуль
вектора суммарного момента сил инерции
второго порядка левого условного
пятицилиндрового двигателя
рМувд!=4,9797aACcos
(2
q>
+18°).
71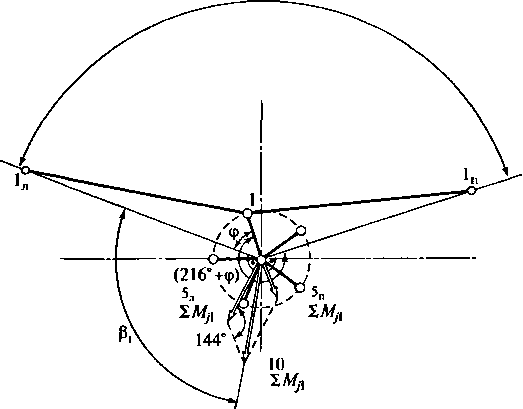
Рис.
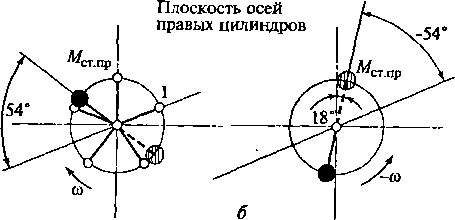
2.32. Синтез механизма уравновешивания
суммарного момента сил инерции
первого
порядка:
а
— схема уравновешивания суммарного
момента сил инерции первого порядка
левого условного шггицилиндрового
двигателя при ВМТ в цилиндре 1Л;
б
— схема уравновешивания суммарного
момента сил инерции первого порядка
правого условного пятицилиндрового
двигателя при ВМТ в цилиндре 1Ц;
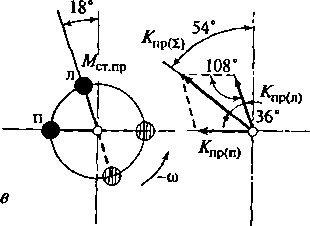
в — схема совмещенного механизма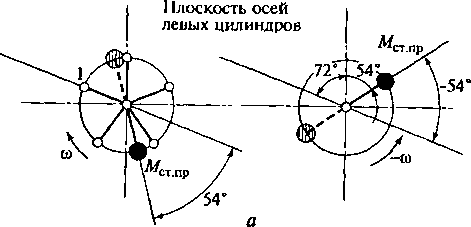

Гис.
2.33. Конструктивная схема механизма
уравновешивания суммарного момента
сил инерции первого порядка
Момент
действует в плоскости осей цилиндров
левого ряда н вектор его направлен
перпендикулярно этой плоскости, как
пока-
ПЮ
на рис. 2.34.
Аналогично,
для правого двигателя:
lEMynwl=4,9797аХС
cos
[2
(</>+216°) 4-18°)] = =4,9797cACcos
(2<р+450°);
иск
гор
его перпендикулярен плоскости осей
цилиндров
правого ряда.
Модуль
суммарного момента сил инррции второго
порядка может быть определен по теореме
косинусов из заштрихованного > it
нового
треугольника (рис. 2.34):
ю
I Г/5 \2 /
5 \2 5 5 -|l/2
М,п1=X
М'ВДJ —
2 X
Мщл)
X Мим
c°s
144°
I
=
=4,9797аХС
[cos2
(2<р
+18°)+cos2
(2ср+450°)
- - 2 cos
(2<р
+18°)
cos
(2ср+450°)
cos 144°]1/2.
73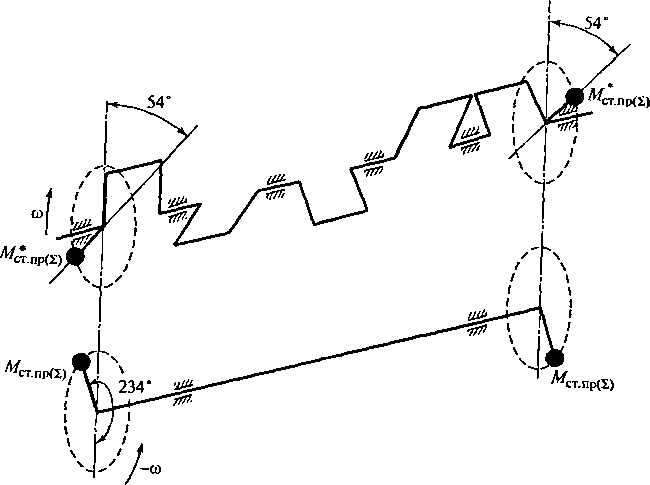
Рис.
2.34. Диаграмма формирования суммарного
момента сил инерции второго
порядка
ю
Направление
вектора момента £М,ц определяется углом
/?2=
= 90°+а2.
Здесь /?2
— угол между вектором момента и
плоскостью
осей
цилиндров левого
ряда;
а2=arcsin sin
144°J.
Для
его уравновешивания необходимо иметь
систему двух встречно вращающихся
валов с угловой частотой ±2со
с установленной на них системой
противовесов (рис. 2.35). Ввиду конструктивной
сложности такие механизмы на практике
не применяются.
^ст.пр(2)
I
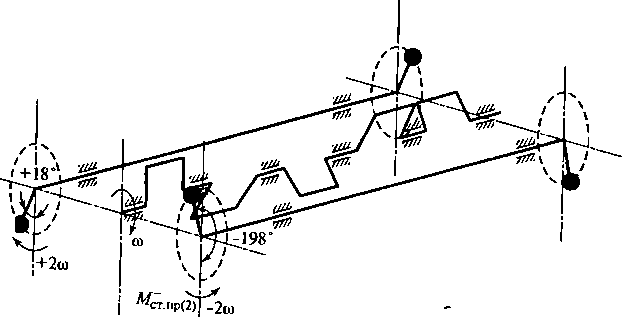
Рис.
2.35. Конструктивная схема механизма
уравновешивания суммарного момента
сил инерции второго порядка.
74
ДВЕНАДЦАТИЦИЛИНДРОВЫЙ
ДВИГАТЕЛЬ С УГЛОМ РАЗВАЛА 60° —12У
(7=60е)
Двигатель
комплектуется шестиколенным
пространственным валом с кривошипами
под углом 120°
(такой же вал имеет шестицилиндровый
линейный
двигатель), что позволяет обеспечить
равномерное, через 60е
чередование рабочих ходов при порядке
работы цилиндров
1л — 6п
— 5л — 2п — Зл —- 4п — 6л
— 1п — 2л — 5п — 4л — Зп — 1л.
Такой
двигатель можно рассматривать как
совокупность двух однорядных
шестицилиндровых двигателей, имеющих
общий коленчатый вал. Так как каждый
из них полностью уравновешен, то и
12V
(5=120°)
также будет полностью уравновешен.
Это справедливо при любом угле развала;
однако равномерное чередование
рабочих ходов будет иметь место лишь
при у=60, 120
и 180°.
ТЕХНОЛОГИЧЕСКАЯ
НЕУРАВНОВЕШЕННОСТЬ ДВИГАТЕЛЕЙ
ВНУТРЕННЕГО СГОРАНИЯ
Проведенный
анализ уравновешенности ДВС различных
схем и типов носит теоретический
характер, так как построен на
|>сдположении
о равенстве всех силовых факторов,
формирующих суммарные силы и моменты.
На практике они будут не- i
колько
отличаться друг от друга в силу
естественных технологических
отклонений при производстве однотипных
элементов дви-
п
геля.
Так,
в многоцилиндровых двигателях вследствие
допустимых < 11
клонений в пределах технологических
допусков могут отличать-
и
массы поршней, а также массы и положения
центра масс
н.1
гунов.
Это
приведет к изменению масс mj=ma+mm(lmjlj)
и
сил инерции
Pj,
принадлежащих
отдельным цилиндрам. Для ограничения
■шриаций rrij
разновесность
поршней, используемых для одного
мпигателя, ограничивается пределами
1...6. При этом поршни сор- щруются по
весовым группам, а для более точной
подгонки в их конструкции предусматриваются
технологические зоны, в которых мечалл
можно удалять.
Шатуны
аналогично сортируются и подгоняются
по массе и понижению центра масс.
Для
определения , и 4,^ шатун в сборе с
вкладышами и шатунными болтами
взвешивается (определяется /Ищ) и затем
устанав
75
Рис.
2.36. Разнесение масс шатуна методом
взвешивания
ливается
своими головками с помо-
щью специальных
кронштейнов на две
чаши весов, как
показано на рис. 2.36.
Добавлением
массы Ат
на чашу
с верхней головкой весы
приводятся
в состояние равновесия.
При этом
/ишп+Ал1=/иш.ж-
Так
как тш:а+тшх=тт,
тшп=
=
1120Пш-^т)
И то
Ап.
и
Для
подгонки шатунов по массе
Шш
и по положению центра масс на
головках
шатуна предусматриваются
места,
в которых металл может быть удален.
Для
устранения технологической
неуравновешенности по силам инерции
вращающихся масс и их моментам коленчатые
валы, маховики, а затем коленчатый
вал в сборе с маховиком подвергаются
динамической балансировке.
Балансировка
вала проводится при установке на
шатунные шейки технологических
масс, имитирующих присутствие на них
приведенных масс шатуна т^.
Балансировка ведется как минимум по
двум плоскостям — по плоскости передней
и задней опор. Лучше, если балансировка
ведется по плоскостям всех кривошипов,
центробежные силы которых
уравновешиваются противовесами.
Кроме
того, уравновешенность двигателя в
значительной мере зависит от разброса
углов между отдельными кривошипами 5.
Наиболее
стабильны эти углы в плоских валах и в
коленчатых налах, получаемых отливкой
из высокопрочных чугунов в оболочковые
формы.
В
кованых валах после разведения кривошипов
на нужный угол необходим тщательный
отжиг заготовки для снятия остаточных
напряжений. В противном случае углы S
по
истечении времени могут самопроизвольно
уменьшаться с непредсказуемым изменением
уравновешенности двигателя.
НЕРАВНОМЕРНОСТЬ
КРУТЯЩЕГО МОМЕНТА
Парно
действующие в системе двигатель —
трансмиссия — подвеска крутящий и
опрокидывающий моменты в силу их
неравномерности по углу поворота
кривошипа могут вызывать переменную
закрутку элементов двигателя и
трансмиссии (крутильные колебания),
а также переменные реакции на опорах
двигателя (его неуравновешенность).
Для суждения о степени равномерности
суммарного 76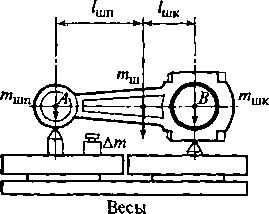
крутящего
момента пользуются коэффициентом
неравномерности крутящего момента fi
=
(М1тлх—М1П^)/Мхср,
где Мх
пшх»
^jpmini
Л/1Ср
— соответственно максимальное,
минимальное и среднее знамения
суммарного крутящего момента двигателя.
Коэффициент
II
изменяет свою величину в зависимости
от режима работы двигателя. Так как
Мхср
пропорционален работе двига- I сля за
цикл, т. е. нагрузке на двигатель, то
знаменатель выражения, описывающего
ц,
определяется нагрузочным режимом его
работы. Числитель же в большей степени
зависит от максимального и минимального
значений сил инерции (обычно его величина
растет i
увеличением
частоты вращения двигателя), т. е. в
основном определяется скоростным
режимом работы двигателя. С учетом
этого различные двигатели сравниваются
по коэффициенту ц
на режиме номинальной мощности.
ц=13,9
у=180°
7=90°
и
i=U
мкрсрп
Y=60°
0 180" 360° 540° 720
Ги>
2.37. Суммарные крутящие моменты
четырехтактных двигателей с искровым
зажиганием и различным количеством
цилиндров (а...е)
77
Из
конструктивных параметров двигателя,
определяющих значение коэффициента
ц,
следует выделить:
число
цилиндров двигателя i;
фактор
равенства угловых интервалов между
рабочими ходами в отдельных цилиндрах.
На
рис. 2.37 приведены кривые суммарных
крутящих моментов однотипных двигателей,
имеющих одинаковые рабочий процесс, D
и
S,
но
различное количество цилиндров i.
Анализ
этих кривых показывает, что fi
резко
уменьшается с увеличением количества
цилиндров.
В
качестве иллюстрации влияния на величину
ц
фактора равномерности чередования
рабочих ходов отметим, что в
шестицилиндровых дизелях с линейным
расположением цилиндров и равномерным,
через 120°, чередованием рабочих ходов
/:= 1,5, в то время как в двигателях 6V
при
у=90°
(чередование рабочих ходов неравномерно:
0=90 и 150°) ^=2,08.
Таким
образом, для обеспечения наилучшей
уравновешенности по опрокидывающему
моменту более предпочтительны двигатели
с равномерным чередованием рабочих
ходов и с большим числом цилиндров.
РАВНОМЕРНОСТЬ
ХОДА ДВИГАТЕЛЯ
Неравномерность
Мт
кроме того, что она вызывает
неуравновешенность двигателя по
Л/оцр,
имеет еще одно негативное для работы
двигателя последствие — она является
причиной неравномерности угловой
частоты вращения коленчатого вала.
Происхождение
этого явления может быть пояснено на
основе анализа баланса моментов на
валу четырехцилиндрового четырехтактного
двигателя, приведенного на рис. 2.38. Для
простоты анализа ограничим
рассматриваемую задачу следующими
условиями:
момент
сопротивления Мс
не изменяется по времени (углу поворота
кривошипа);
режим
работы двигателя — установившийся;
индикаторный момент равен моменту
сопротивления Mi=Mip_cp=Mc;
при
этом средняя угловая частота остается
неизменной;
момент
инерции всех подвижных элементов
двигателя J0,
приведенный
к оси коленчатого вала, не изменяется
по времени.
В
этом случае на коленчатом валу в любой
фазе рабочего цикла Л/jp—Мс=Мт;
Мх
~ Мс=J0e=J0(da>/dt),
где
Мт
— инерционный момент; в
— угловое ускорение системы коленчатый
вал — маховик.
78
Из
приведенного выше уравнения следует,
что в моменты времени, когда МТ?=МС
(точки 1...8
на рис. 2.38), dw/dt=0.
Это соответствует экстремуму угловой
скорости.
Качественный
анализ показывает, что если этому
предшествова- iio
МХ>МС
и da>ldt>0,
то
в этих точках (2,
4, 6, 8)
будет соответственно, если МХ<МС
и dco/dt<
0,
то будет Шщь (точки 1,
3,
Приведенные
рассуждения свидетельствуют о
неизбежности возникновения
неравномерности угловой скорости
вследствие переменности по углу
поворота кривошипа крутящего момента
двигателя.
Неравномерность
со
оценивается коэффициентом
неравномерности хода двигателя
&=(союш—согщВ)1соср.
Для
нахождения зависимости <5 от
конструктивных и режимных факторов,
характеризующих работу двигателя,
проинтегрируем уравнение баланса
моментов на участке от <р1~£Цтш
до q>i~com.,
(см.
рис. 2.36). После разделения переменных
с учетом того, что
(dtojdt)=(dco/dcpXdcp/dt)=ca(dwjdcp)=1
/2(dco2ldq>),
получаем
Обозначив
| (Mt—Mc)dcp
через
избыточную работу Атб
(зашт-
«>i
рихованная
площадка на рис. 2.38) и выполнив
интегрирование правой части, получим
После
преобразований с учетом того, что
соГр»1/?(шт„+аиА
имеем Asa6=J0a>ZpS,
откуда
S=Am6/(J0o}^). 4
Данная
зависимость иллюстрирует конструктивные
параметры, с помощью которых возможно
управление величиной 5
при разработке двигателя. Это в
первую очередь варьирование числом
цилиндров и фактором равномерности
чередования рабочих ходов, от которых
исключительно зависит величина Ашб,
а при принятой компоновочной схеме
двигателя — изменение J0.
Для
получения требуемого д
в конструкции двигателя предусматривается
маховик, при использовании которого
J0«J„,
т.
е. практически весь момент инерции в
этом случае сосредоточен в маховике.
7).
*^изб
— /2^o(^max I max ®mmX®max ^minX^cp/^cp)-
79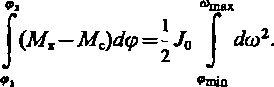
Ряс.
2.38. Баланс моментов на валу четырехтактного
четырехцилиндрового двигателя на
установившемся режиме работы
Увеличением
/м
можно получить сколь угодно малую
величину S.
Однако
в автомобильных двигателях не всегда
целесообразно использовать маховики
с большим /м,
так как это приводит к возрастанию
инерционности и замедляет процесс
перехода его с режима на режим, особенно
при разгоне. При этом могут существенно
ухудшиться динамические характеристики
автомобиля в целом.
Для
тягачей и тракторов, в которых приемистость
не имеет первостепенного значения,
величина /м
определяется из условия плавности
трогания с места при включенном сцеплении
и рабочем положении буксировочного
устройства.
В
соответствии с этим в современных
конструкциях транспортных средств
для автомобильных двигателей
5=0,02.-0,025, для двигателей тракторов и
тягачей 6=0,005...0,01.
При
подборе маховика автомобильного
двигателя часто используют так
называемый безразмерный
момент инерции ф
=
80
=
Л(^том/Л/ж.вом> который для махо-
виков
большинства двигателей авто-
мобилей
варьируется в сравнитель-
но узких
пределах, так что с доста-
точной для
практики точностью мо-
жно полагать
фж
const.
Здесь
Мсл0м
и ®ном
— соответст-
венно эффективный
момент и часто-
та вращения коленчатого
вала на
режиме номинальной мощности.
На
этом основании /мда
%)Д(М„ом/ш1ол1),
где юн=яляом/30;
яНом
— число оборотов в минуту ко-
ленчатого
вала на расчетном режи-
ме;
\J/
—
200...350. Рис.
2.39. Определение действитель-
IIри
конструировании маховика ного
момента инерции маховика его
фактический момент инерции
/м.д
должен быть равен /м.
Величина /м
д
с достаточной практической точностью
может быть определена делением тела
маховика на N
кольцевых
элементов с простейшей геометрией
сечения, как это показано на рис. 2.39.
N
В
этом случае /м
д«
£ щг?,
где mt
и
г, — соответственно масса i=i
и
расстояние от оси вращения до центра
поперечного сечения /-го кольцевого
элемента.
ОСНОВЫ
АНАЛИЗА И АМОРТИЗАЦИИ КОЛЕБАНИЙ
ДВИГАТЕЛЯ НА ПОДВЕСКЕ
СИЛОВЫЕ
ФАКТОРЫ, ВЫЗЫВАЮЩИЕ КОЛЕБАНИЯ ПОРШНЕВЫХ
ДВС НА ПОДВЕСКЕ
Как
следует из рис. 2.40, колебания двигателя
на элементах его фиксации на раме или
кузове автомобиля (трактора,
дорожно-строительной машины) могут
возбуждаться во-ми силовыми факторами,
вызывающими неуравновешенность
двигателя. Также может иметь место
кинематическое возбуждение колебаний
со стороны шасси при наезде транспортного
средства на препятствие (/?„).
Во
втором случае колебания возникают в
конструкции всей транспортной единицы,
и их анализ выходит за рамки настоящего
курса. Поэтому здесь ограничимся
изучением колебаний от
81
/и4
тъ
т2
г3
Л«д~
1=1
Рис.
2.40. Силовые факторы, вызывающие колебания
двигателя на подвеске
неуравновешенных
сил инерции ЕРуь ЕР/п, ЪК,
их моментов ЕА/д, ’LMjn,
ЕЛ/„
а также опрокидывающего момента Л/опр.
Для
уменьшения количества энергии,
передаваемой от колеблющегося
двигателя на экипаж и наоборот, ДВС
виброизолиру- ют от кузова (рамы) с
помощью установки его на систему упругих
элементов, называемую подвеской.
Однако при этом возможно возрастание
амплитуд колебаний самого двигателя
до величин, нарушающих работоспособность
его элементов и систем.
Таким
образом, задача
проектирования подвески
может быть сформулирована следующим
образом: минимизация количества энергии,
которая передается системе двигатель
— подвеска — экипаж при сохранении
на практически приемлемом уровне
амплитуд вибраций двигателя.
РАСЧЕТНАЯ
СХЕМА ДВИГАТЕЛЯ, КОЛЕБЛЮЩЕГОСЯ НА
ПОДВЕСКЕ
Расчетные
исследования колебаний в системе
двигатель — подвеска требуют замены
ее упрощенной динамически эквивалентной
моделью, в которой сохраняются только
существенные для данного расчета
свойства объекта.
Анализ
колебаний двигателя на подвеске принято
проводить при следующих основных
допущениях:
двигатель
(силовой агрегат) полагается абсолютно
жестким (недеформируемым) телом;
82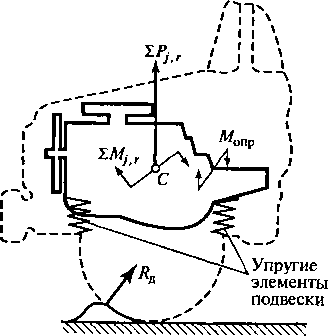
рама
(кузов) полагается абсолютно жесткой
и имеющей бесконечно большую массу;
начало
системы координат совпадает с центром
инерции силового агрегата, оси
координат являются центральными.
В
этом случае (рис. 2.41) под действием
перечисленных выше силовых факторов
двигатель совершает шесть возможных
колебательных движений: три
поступательных в направлении осей
х=х(/),
V=y{t),
z=z(t)
и три угловых относительно этих осей
(p=<p(t),
а=
Для
выполнения качественного анализа
явлений, определяющих характер колебаний
двигателя на подвеске, рассмотрим
простейший случай — колебательное
движение ДВС относительно координаты
v
под
действием силы инерции первого порядка
ЕРд=Л cos<p
= =A
cos
(cjt)
(рис.
2.42).
Полагая
для простоты 1\
= /2
и жесткость левого упругого элемента
Си
равной жесткости правого элемента С2,
получим расчетную схему, соответствующую
колебательной системе с одной степенью
свободы. После введения в систему
элемента, обозначенного на рис. 2.42 через
г]
и имитирующего неупругие потери энергии
колебаний в системе, с учетом принципа
д’Аламбера составим уравнение баланса
сил:
1цесь
т
— масса двигателя; Pm=m(d2x/dt2)
—
сила инерции; Ржп=
-r(dxjdt)
—
сила неупругих потерь; r=2rjm;
t]
= Wnor/WaoBt
—
коэф-
или
т
(d2x/dt2)+г
(dx/dt)+ZСх=А
cos
(at).
h
h
1’нс.
2.41.
Схема
амортизированного двигателя
1
Рис. 2.42. Расчетная схема колебаний
двигателя на подвеске относительно
одной из обобщенных координат — оси х
83
![]()


фициент
неупругих потерь (IVnoT
—
энергия, рассеиваемая в системе;
JVnoi№
—
энергия, подводимая к колебательной
системе); Ру,ф=
=ХСх
— упругая сила деформированных упругих
элементов.
Отсюда может быть получено
уравнение движения амортизирован-
ного
двигателя относительно координаты х:
(dzx/dt2)+2r](dx/dt)+со2х=а
cos
(cot),
где
(По=у/хС/т
— частота собственных колебаний
системы; а=
—А/т.
Решение
этого уравнения известно:
х=—
— ~
у/(со2—сОц)2+4
tj2co2
где
со
— круговая частота возмущающей силы
(в данном случае
она совпадает с
угловой скоростью коленчатого вала);
ф
=
=arctg
[2r}co/(co2
—
to2)]
—
фазовый сдвиг между перемещением и
вы-
нуждающей силой 2.Pfl.
Отвлекаясь
от фазы колебаний, несущественно
влияющей на
энергетические оценки,
решение может быть записано в следующем
виде:
х—К(со)Т.Рл,
где К(со)=(у/(со2—со2)2+4т}2со2)~1—функция
передачи
колебательной системы. Фактически К
(со)
является часто-
тно-зависимым
коэффициентом про-
порциональности
между перемеще-
нием и силой,
возбуждающей коле-
бания. Бе величина
при фиксирован-
ном значении со
определяется ис-
ключительно
упругомассовыми ха-
рактеристиками
колебательной си-
стемы, такими, как
m,
ZC,
Т].
Графи-
ческая зависимость K(co)=f(co),
при-
веденная
на рис. 2.43, показывает,
что ее значение
изменяется в зависи-
мости от
скоростного режима рабо-
ты двигателя,
достигая максимума
при ш=ш0
(со=тш/30; п — число
оборотов коленчатого
вала в мину-
ту). Численное значение
А^(а»)тал
ш=у
= ^ определяется коэффициентом неуп-
ругих
потерь в системе I/. Чем ниже
Рис.
2.43. Частотная диаграмма фу- уровень
неупругих потерь, тем боль-
нкции
передачи колебательной си- ше
/^(ш) • при
отсутствии потерь
сгемы
с о двои степенью свободы , т//<
(»7
= 0)
К(ш)т«-»со.
Afro)
Зона
рабочих
режимов
ДВС
й>»0>0
(п»пй)
84~
- - -
= cos
(cot—
ф),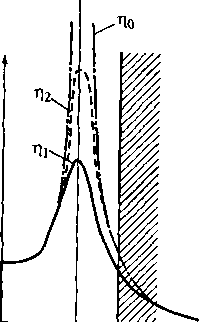
Отсюда
следует, что наибольшая амплитуда
колебаний и максимум колебательной
энергии, передаваемой на экипаж,
достигаются при совпадении (резонансе)
частот возмущающей силы и собственных
колебаний системы (и=ЗОсо/я=«о=ЗОшо/л).
Для исключения резонанса необходимо
либо не допускать работу двигателя с
л=п0
(обычно л» По), либо понижать частоту
собственных колебаний По
до выполнения отмеченного выше условия.
ПОНЯТИЯ
ОБ ОСЯХ, ЦЕНТРЕ ЖЕСТКОСТИ ПОДВЕСКИ И
СВЯЗАННЫХ КОЛЕБАНИЯХ
Анализ
колебаний ДВС на подвеске относительно
оси х,
выполненный в предыдущем параграфе,
базировался на допущениях о равенстве
А=/2
и Ci
=
С2.
Благодаря этому в рассматриваемом
случае сила ЪРп
вызывала смещение двигателя только в
направлении оси х,
что, вообще говоря, является лишь частным
случаем. Невыполнение любого из
оговоренных выше условий приведет к
тому, ч го сила, направленная строго в
направлении оси х,
вызовет смещение двигателя относительно
двух (или более) координат. Для пояснения
этого рассмотрим колебания ДВС, изменив
жесткость задне- ю упругого элемента
так, чтобы С2=2С]
(рис. 2.44).
Простейший
анализ показывает: для данных
условий, учитывая, ч го реакции на опорах
возникают за счет их упругой деформации,
получим Ri
=
CiAj
~R2=
С2А2
и,
следовательно,
А2=A^Ci/Q)=1/2А].
1десь А] и Л2
— деформации соответственно 1-й и 2-й
опор. Это ошачает, что в данной ситуации
силовой фактор, действующий относительно
одной из координат (х), вызывает смещение
двига- I еля одновременно относительно
двух координат — оси х
и поворота на угол Р
относительно оси z.
Такие
колебания носят название <)вухсвязанных
(в общем случае многосвязанных).
Нежелательность
феномена связанности колебаний очевидна.
На практике уменьшить или, наоборот,
усилить эффект связанности колебаний
возможно изменением положения линии
действия возбуждающей силы. В пределе
линию действия можно ориентировать
относительно элементов подвески таким
образом, что направленный вдоль нее
силовой фактор будет выбывать смещение
двигателя юлько относительно одной из
осей координат (на рис. 2.45 относительно
оси х).
В данном примере это имело бы место при
направлении возбуждающих сил вдоль
оси, разделяющей расстояние между
опорами в отношении 2:1 (/i
= 2/2).
Тогда
i?2=A2C2=
2Д,
=2А!С!, а так как С2=2СЬ
то А, = А2.
Это направление носит название оси
жесткости подвески.
85
Рис.
2.44. Схема возникновения связан- Рис.
2.45. Схема размещения оси жест- пыл
колебаний кости подвески, параллельной
оси х
Принципиально
их может быть три — это оси жесткости,
параллельные осям координат х,
у
и z.
Они
могут пересекаться в одной точке (не
обязательно!), которая в этом случае
носит название центра
жесткости подвески.
Так
как связанность колебаний — явление
нежелательное, то при проектировании
подвески и выборе количества, размещения
и характеристик упругих элементов
необходимо стремиться к совмещению
центра масс двигателя (куда приложены
инерционные силовые факторы, возбуждающие
колебания) с центром жесткости подвески
(при его наличии) или совпадению его с
наибольшим количеством осей жесткости.
ОСНОВНЫЕ
ТРЕБОВАНИЯ К КОНСТРУКТИВНЫМ ПАРАМЕТРАМ
ПОДВЕСКИ
При
проектировании подвески необходимо,
чтобы ее конструкция удовлетворяла
следующему минимуму требований:
количество,
размещение и упругие характеристики
элементов подвески должны обеспечивать
отсутствие собственных резонансных
колебаний в диапазоне частот вращения
коленчатого вала выше минимальных
устойчивых оборотов холостого хода
двигателя (зона рабочих режимов
двигателя на рис. 2.43);
материалы
и конструкция упругих элементов должны
обеспечивать наибольший уровень
неупругих потерь (наибольшие величины
17);
при
проработке конструктивных вариантов
предпочтение следует отдавать тем
из них, в которых наблюдается совмещение
центра масс с наибольшим количеством
осей жесткости.
86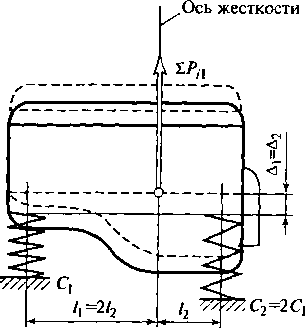
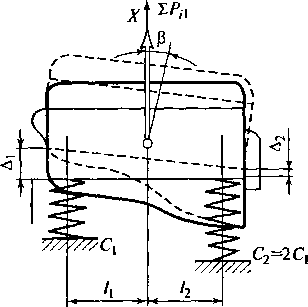
а
б
Рис.
2.46. Схема подвески (а)
и
вариант конструкции упругих элементов
(6)
автомобильного двигателя
На
рис. 2.46 в качестве примера приведены
схема размещения и вариант конструкции
упругих элементов подвески автомобильного
двигателя.