
- •Глава 1 кинематика и динамика кривошипно-шатунного механизма
- •Глава 2 уравновешенность и уравновешивание двигателя
- •Глава 3
- •Глава 4
- •Глава 5 поршневая группа
- •53. Поршневые кольца
- •Глава 6 шатунная группа
- •Глава 7 коленчатый бал
- •Глава 8
- •8.9. Потери энергии при колебаниях
- •Глава 9
- •Глава 10 смазочная система
- •Глава 11 система охлаждения
- •Глава 12 система воздухопитания
- •11.1. Агрегаты воз ду хопитания двигателей с наддувом (компрессоры, турбокомпрессоры)
- •Глава 13 система выпуска
- •Глава 14 система пуска двигателей
- •Глава 15
- •Глава 16 принципы подбора двс д ля транспортного средства
- •Глава 1. Кинематика и динамика кривошипно-шатунного механизма 5
- •Глава 2. Уравновешенность и уравновешивание двигателя 31
- •Глава 3. Основы конструирования и предпосылки к расчету деталей двигателя
- •Глава 4. Цилиндровая группа • картеры 69
- •Глава 5. Поршневая группа 87
- •Глава 6. Шатунная группа 123
- •Глава 7. Коленчатый вал 136
- •Глава 8. Колебания коленчатых валов 152
- •Глава 9. Механизм газораспределения 179
- •Глава 10. Смазочная система 215
- •Глава 11. Система охлаждения 233
Резонанс
будет иметь место, если число колебаний
в минуту крутильной системы п0„
соответствующее круговой частоте
ее собственных колебаний данной формы
П„ совпадет с щ.
для какой-либо гармоники в рабочем
Такая
диаграмма представляет собой пучок
прямых, каждая из которых соответствует
собой
соотношением и, =- кп
п*,
х
нм/м
[кол/мин].
одному
порядку гармоник
nPlf
Г>р3
пК
п.мин
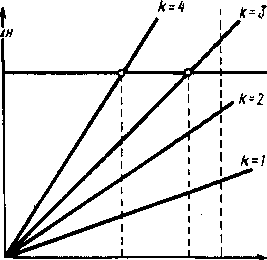
Рис.
8.10. Определение резонансных р жимов
работы
двигателя по
частотнс
диаграмме
диапазоне
частот вращения дви-
гателя. Величины
Па
и П/ связаны между собой соотношением
На
рис. 8.10 показан порядок определения
резонансных режнмо работы двигателя
и резонирующих гармоник при собственной
чг стоте i-й
формы собственных колебаний п^. Это
частота вращеии коленчатого вала
двигателя npJ,
где
резонирует 3-я гармоника, и пр
где
резонирует 4-я гармоника.
При
анализе характера движения элементов
крутильной систем! отмечалось, что при
совпадении частоты вынуждающей силы
с о; ной из собственных частот системы
амплитуды смещения ее «моте рных» масс
бесконечно возрастают. На практике
такое явление н наблюдается в силу
того, что амплитуды угловых колебаний
огрэ ничиваются возникающими при
колебаниях потерями энергии.
Рассмотрим
структуру одного из написанных ранее
уравнен и движения крутильной системы:
По
своей физической „сущности члены,
входящие в уравненш представляют собой:
/Д= Мт
— инерционный момент; С, (в,
-
0j+1)
—
С,-1
(0,-+1
— в,)=Мущ,
~
упругий момент; М,
— возбуждэ ющий момент М в.
Таким
образом, При совершении системо
свободных
колебаний = 0) имеем Л/ии
= Л/упр.
При
наличии колебаний с потерями энергии
в уравнение момек
=
60П;/(2тс)
ft;
9,5
5 Ц.
J,в,
+ С, (в,-8i+
0-
С,_, (в,-,-$,)=
м.![]()
8.9. Потери энергии при колебаниях
тов
необходимо добавить момент
сопротивления который
учитывал
бы необратимые потери энергии в системе:
-Л/ял
4" = Л/воэ5.
С
учетом того, что М^—Мущ,,
М„,пр
= Л/кгй,
это означает, что при колебаниях работа
внешних сил идет на преодоление неупругих
сопротивлении в системе, если форма
вынужденных колебаний совпадает с
формой собственных колебаний. Основными
факторами, вызывающими потери энергии
при колебаниях в крутильных системах
ДВС, являются переменные силы жидкостного
трения в подшипниках и цилиндрах,
которые пропорциональны скорости
относительного перемещения сопряженных
деталей, а также силы внутреннего трения
в материале коленчатого вала (упругий
гистерезис), зависящие от амплитуды
угловых колебаний его элементов.
В
ДВС вследствие небольшого объема вала
потери энергии на внутреннее трение
невелики. Поэтому при практических
расчетах полагают, что момент сопротивления
пропорционален скорости колебаний:
Мат
= £9,
где
£ — коэффициент демпфирования,
учитывающий все виды неуп- ругих потерь.
Значение
£ расчету не поддается и определяется
на основе статистических
экспериментальных данных do
коэффициентам
демпфирования для двигателей
аналогичной конструкции.
Для
поршневых двигателей удовлетворительные
результаты дает формула Видлера
С
= 0,79)10
‘г
Ч,
где
D
—
диаметр цилиндра, см; г
— радиус кривошипа, см; i
—
количество цилиндров; (i
—
удельный коэффициент демпфирования,
кг • с/см3,
fi=0,015...0,02
— для автомобильных двигателей.
Рассмотрим
характер движения крутильной системы
с учетом момента сопротивления. Для
простоты ограничимся случаем воздействия
на «моторные» массы одной грамоники
крутящего момента. В силу того что
при добавлении Л/юар
уравнения движения остаются линейными,
общий характер движения системы также
может быть определен как суперпозиция
движений, вызываемых отдельными
гармониками, составляющими крутящий
момент. Вообще же случай моногармонического
воздействия на крутильную систему
нам наиболее близок, так как в конечном
итоге необходимо рассчитать амплитуды
относительных смещений масс при
резонансных колебаниях. Так как
одновременно может резонировать
только одна гармоника, то это как раз
суть рассматриваемого здесь случая.
Уравнения
движения системы с неупругими
сопротивлениями:
170
Система
п
(i=
1,
2, л),
JjS,
+ E,6j+Ci (di
— вц
])
— Ci~i
(0<_]
—
0,)
= M,sm
Так
как величина неупругих потерь в
крутильных системах ДВС относительно
невелика, то влияние Л/„щ, на формы
собственных колебаний должно быть
также невелико. Это подтверждается и
дан* ными многочисленных теоретических
и экспериментальных исследовании;
при резонансе форма вынужденных
крутильных колебаний коленчатого вала
практически полностью совпадает с
формой свободных его колебаний.
Тогда,
согласно принятому допущению, при
резонансе все массы крутильной системы
с потерями колеблются синфазно и решение
данной системы по аналогии с выводами
§ 8.4 будет иметь вид
Основное
отличие данного решения от решения для
системы без потерь состоит в том, что
за счет рассеивания энергии амплитуды
смещения соответствующих масс Л
* будут меньше, а сдвиг фаз не будет
однозначно определяться фазами гармоник
моментов, действующих на отдельные
кривошипы [<р, в (§ 8.4)], и зависит от
диссипативных свойств и режима
колебаний системы уг
= * + е, где £ — добавочный сдвиг фазы за
счет наличия в системе неупругих потерь.
Величина его изменяется в зависимости
от коэффициентов потерь в системе и
соотношения частот возбуждающей силы
и собственных колебаний системы.
Принятое
допущение позволяет значительно
упростить процесс определения амплитуд
закрутки отдельных участков вала при
резонансных колебаниях. В данном
случае необходимо рассчитать только
амплитуду смещения первой «моторной»
массы, так как в силу эквидистантности
формы резонансных и свободных колебаний
остальные амплитуды могут быть определены
через относительные их значения.
Кроме
того, из данного допущения следует,
что, поскольку при резонансе крутильная
система совершает установившиеся
колебания, форма которых подобна
форме свободных ее колебаний, работа
возбуждающего момента будет равна
работе моментов сопротивления, так
как в этом случае равны между собой
работы инерционных и упругих моментов.
Это обстоятельство и используется
на практике для нахождения амплитуды
первой «моторной» массы.
171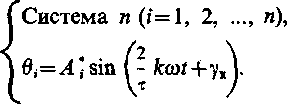
8ч
10. РАБОТА ВОЗБУЖДАЮЩЕГО МОМЕНТА И
МОМЕНТА СИЛ СОПРОТИВЛЕНИЯ
Работа
возбуждающего момевта ыа одном нз колен
вала (для примера на /-м) за один период
колебаний Гж=—:
ка>
J
A^det—
J
AfjSin
0 ka>t+<p(^j
d^'sin
0 faa/+y,^|; Работа
возбуждающего момента на всех л коленах
вала
w<&=t
w^n f
лм;«п(*«-*)=
(-1
i-i
iiMt,
[cosy, J] Asiny,
£Л*соз^М
=
V j-i f-i
/
=nM* sin (y, - (p
I),
Я
2
Л/яп?»
где y,=arctg .
£
(-t
Так
как при резонансе величина работы
достигает максимума что имеет место
при (у,— <р^)
= л12,
то в этом случае работа возбуж дающего
момента равна
лД/т
^yjjC
А
* c°s
j + ^ J sin <jt> J
.
Работа
момента сопротивления на i-м
колене за период колебания Гж:
Гг Ъ
w%р
= | d0(=
| d
[а
; sin
0
кш
+ =
о о
*^|^;cos0 кхоА]
cos
0
£<о*+уж^
d
0
fca)f+yr^;
W«L
= nt - Ш
(A
J)2.
T
172
Суммарная
работа момента сопротивления на всех
п
коленах
*4
- Ьа =
ка
£ {А*,)1.
/-1
х
х
«-1
ОПРЕДЕЛЕНИЕ
АМПЛИТУД УГЛОВЫХ СМЕЩЕНИЙ «МОТОРНЫХ»
МАСС КРУТИЛЬНОЙ СИСТЕМЫ
В
соответствии с принятым допущением
при резонансе (FFS*
=
-IPS,):
пМх
Это
же выражение может быть записано в
относительных амп литудах (А,
= щА
■). Отсюда находится амплитуда смещения
перво] «моторной» массы:
|
4 £ Я(ЯПф«1 м-l -I |
2 |
Я |
- У а? |
|
* |
-1 |
Величины действительных амплитуд вынужденных угловых ко лебаенй остальных масс определяются умножением на A j величинь относительных амплитуд.
ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В ЭЛЕМЕНТАХ ВАЛА ОТ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Дополнительные напряжения скручивания, возникающие в ко ленчатом валу от резонансных крутильных колебаний, определяю по упругому моменту, действующему в наиболее напряженно!* участке вала:
•Муир
>
где Л/уцр—С, (A t —А *+|) — наибольшее значение упругого момент; в узле колебаний; С, — жесткость /-го участка вала, на которои» расположен узел колебаний; A A j+1 — амплитуды угловых смеще ний I-б и (/+ 1>й «моторных» масс, ограничивающих 1-й участи вала; №# — момент сопротивления скручиванию расчетного участ ка вала.
17:
СПОСОБЫ СНИЖЕНИЯ НАПРЯЖЕНИЙ В КОНСТРУКЦИИ ВАЛА ОТ КРУТИЛЬНЫХ КОЛЕБАНИЙ
В том случае, если результаты расчета коленчатого вала на крутильные колебания, подтвержденные испытаниями, показали, что напряжения в его конструкции превышают допустимые, необ- ходимо устранить вредное влияние крутильных колебаний одним из следующих способов:
для четырехтактных двигателей, у которых при выбранном расположении колен вала имеется несколько возможных вариантов порядка работы, необходимо выбрать такой из них, который обес- печивал бы фазовые углы возбуждающих гармоник, дающие на- именьшие значения равнодействующего вектора относительных ам-
плитуд смещений:
"я ~j2 Г я
£a,cos<p£° -Н £a;sin<p<°
J Li-i
(см. формулу для расчета амплитуды смещения первой «моторной» массы A j в § 8.11);
ф изменить конструкцию коленчатого вала (при неизменной кривошипной схеме) с целью повышения частоты собственных колебаний системы и вывода ее за пределы рабочего диапазона частот вращения двигателя. Для этого необходимо стремиться уменьшить моменты инерции «моторных» масс, а также повысить крутильную жесткость коленчатого вала;
ф если указанные мероприятия не дают желаемого результата или не могут быть практически осуществлены, на коленчатом валу устанавливают специальные гасители крутильных колебаний.
По способу воздействия на крутильную систему коленчатого вала гасители делятся на два типа: 1) гасители без поглощения колебательной энергии системы — маятниковые (динамические) гасители, или антивибраторы; 2) гасители с частичным поглощением и последующим рассеиванием энергии крутильных колебаний в окружающую среду в виде теплоты — демпферы.
Гасители первого типа работают по принципу расстройки резонансной системы коленчатого вала. Поэтому они эффективны только в узком диапазоне частот на одном режиме работы двигателя (резонансный режим). На остальных режимах они могут, наоборот, даже увеличивать размах колебаний коленчатого вала. Поэтому они применяются в основном в стационарных двигателях, работающих на постоянном скоростном режиме.
Гасители второго типа работают по принципу увеличения неупругих потерь (затухания) в крутильной системе двигателя. Дополнительное поглощение энергии колебаний осуществляется либо за
2
-►mm
![]()
174
счет
увеличения сухого тре-
ния в системе
(гасители су-
хого трения), либо за
счет
жидкостного трения (гасите-
ли
жидкостного трения), ли-
бо за счет
внутреннего тре-
ния (молекулярного
трения)
в упругом элементе
гасителя
(резиновые гасители).
Схема
наиболее распространенных
в
автотракторных двигате-
лях гасителей
молекулярно-
го а жидкостного
трения
приведена на рис. 8.11.
Гасители
колебаний вто-
рого типа уменьшают
амп-
литуды
колебаний при любой частоте вращения
двигателя, включая
и резонансную
частоту. Поэтому демпферы нашли широкое
приме-
нение на многорежимных
двигателях, в частности на автотрактор-
ных.
ОСНОВНЫЕ
СВЕДЕНИЯ ОБ ИЗГИБНЫХ КОЛЕБАНИЯХ
КОЛЕНЧАТЫХ ВАЛОВ
В
поршневых двигателях внутреннего
сгорания наряду с крутильными имеют
место нзгибные колебания коленчатого
вала, при которых его элементы периодически
смещаются друг относительно друга в
направлении, перпендикулярном продольной
оси. Это явление приводит к возникновению
дополнительных знакопеременных
изгибающих напряжений, нагружающих
коленчатый вал, что в ряде случаев может
являться причиной его поломки. Для
большинства современных ДВС изгибные
колебания не оказывают существенного
влияния на работоспособность конструкций;
их действие становится заметным
лишь в высокофорсированных быстроходных
двигателях. Поэтому в настоящее время
проблема изгибных колебаний является
сравнительно новой для двигател ест
роения, чем и объясняется малая
изученность этого явления.
Основной
причиной, приводящей к появлению
изгибных колебаний в коленчатых
валах ДВС, является взаимодействие
радиальных составляющих газовых и
инерционных сил с упругой системой
коленчатого вала.
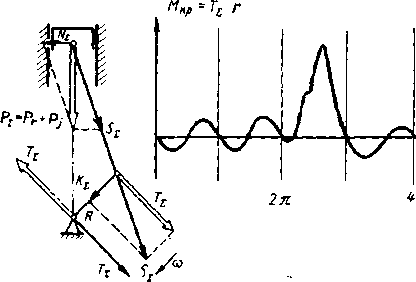
На
каждый кривошип со стороны шатуна
действует продольная сила S=f
(Pt,
Pj)
(рис. 8.12). Ее составляющая К,
направленная по радиусу кривошипа,
изменяется по сложному периодическому
закону с периодом Т=т7г/(2<о),
где
о
—
угловая
частота вращения
Рве.
8.11. Схема гасителей крутильных коле-
баянй:
а
— молежуляряого грени* {I
— авершюявый элемент, 2
— упругий элемент); 6
— жидкостного тре- ввя (/ — дидгай
наполнитель — саликон)
175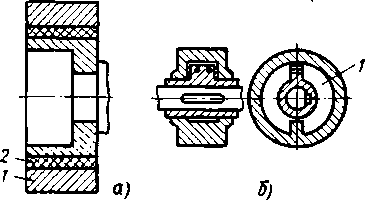
ip=u)t
Рис.
8.12. Возникновение вэгибиых колебаний
крнвошяпа от действия силы К,
коленчатого
вала. Как и всякую периодическую функцию,
ее можнс представить бесконечным
гармоническим рядом:
где
к=0,
I, 2, 3, Кь
и щ
— соответственно амплитуда и фаза
fc-fi
гармоники
силы К.
Коленчатый
вал в делом и каждый его кривошип в
отдельности представляют собой упругую
изгнбную систему, которая имеет множество
собственных форм и соответствующих им
частот со
бственных
колебаний а)0.
В случае совпадения частот и одной
из
гармоник силы К
с одной из собственных частот системы
со0
амплитуда изгибных колебаний может
стать опасной для прочности коленчатого
вала.
Поэтому
особенно интенсивные изгибные колебания
характерны для высокооборотных ДВС.
Для большинства современных ДВС наиболее
интенсивны первые 12... 16 «моторных»
гармоник силы А
й>о»"
£<у,
но с увеличением частоты вращения
растут значения со
и
соответственно одна из гармоник может
по частоте совпасть с о>0,
что приведет к резонансным изгибным
колебаниям.
Рассмотрим
основные предпосылки к расчету коленчатых
валов на изгибные колебания. В настоящее
время отсутствуют достоверные
методы, позволяющие до конца провести
расчет коленчатых валов ДВС на изгибные
колебания, т. е. определить амплитуды
смещений отдельных участков вала и
рассчитать дополнительные изгибные
напряжения, возникающие в его элементах.
Существующие методики позволяют
лишь оценить возможность возникнове
И6
![]()
![]()
ния'в
упругой системе вала
резонансных
изгибных ко-
лебаний в пределах
рабоче-
го диапазона частот враще-
ния
двигателя. Расчет при
этом сводится
к определе-
нию частот собственных
колебаний
(чаще всего то-
лько первой формы) и
по-
следующего их сравнения
с
частотами возмущающих
факторов.
Как
и в случае крутиль-
ных колебаний,
расчет ко-
ленчатого вала на изгиб-
ные
колебания начинается
с составления
упрощенной
эквивалентной колебатель-
ной
системы. Наиболее употребительной
является эквивалентная
схема,
представляющая собой невесомый упругий
вал с сосредото-
ченными в середине
каждого пролета массами (рис. 8.13).
Пред-
полагается, что вал призматически
оперт в точках, соответству-
ющих
центрам коренных шеек. Условия приведения
действитель-
ного коленчатого вала
к его эквивалентной динамической модели
те
же, что и при расчете крутильных
колебаний, т. е. равенство кине-
тической
и потенциальной энергий колеблющихся
элементов вала
и сопряженных с ним
элементов КШМ массам эквивалентной
систе-
мы. Из >тих условий определяются
массы (т>)
к изгибиыс жесткости
(С,) на отдельных
участках расчетной модели,
соответствующих
пролету вала между
коренными опорами. Достоверные
методы
расчета изгибной жесткости
кривошипов коленчатых валов в насто-
ящее
время отсутствуют, что объясняется
сложностью учета влия-
ния соседних
участков вала. Поэтому для их определения
использу-
ют экспериментальные
методы, заключающиеся в нагружении
кри-
вошипа в центре шатунных шеек
коленчатого вала аналогичной
конструкции.
Коленчатый вал при этом оперт призматически
в цен-
трах коренных опор. Замеряя
величину прогиба у
над точкой при-
ложения нагружающей
силы Р,
вычисляют жесткость данного кри-
вошипа:
Cj—Pjy,
Таким
способом определяется жесткость всех
уча-
стков коленчатого вала.
При
расчете эквивалентных масс учитываются
массы КШМ, относящегося к данному
расчетному участку.
После
определения параметров эквивалентной
расчетной модели (т,) и (С,) переходят
к определению частот собственных
колебаний, расчет которых ведется при
следующих допущениях:
ф
неупругие потери при изгибных колебаниях
отсутствуют;
Рис.
8ДЗ. Экаоталеатаая схема для анализа
изгибных колебаний коленчатого вала
177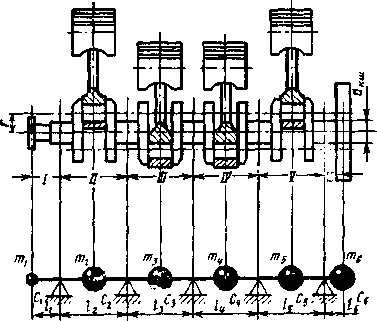
каждый
участок эквивалентной расчетной модели
дннамйчес ки независим от остальных
участков.
С
учетом сделанных допущений движение
(собственные кОлеба ння) эквивалентной
модели опишется системой л независш^ых
од нородных линейных дифференциальных
уравнений (л — количестве самостоятельных
участков расчетной модели):
(Система
п
(* = 1, 2, .... л),
(т^+О^О,
где
/ — номер расчетного участка; ук
— смещение /-й сосредоточен ной массы.
Решение
этой системы известно:
[Система
tt
(/**
I, 2, л),
[yt-Ai
sin (ш«г
+ ^),
где
с% — частота собственных нзгибных
колебаний i-ro
участка.
После
подстановки данных решений в исходную
систему уравне няй получим
(Система
л (i=
1,
2, ..., и),
В
расчет принимается наиболее низкое
значение а>с
из всего го множества и.
Полученное
значение Одкш изгибных колебаний
коленчатого вала затем проверяют
на возможность резонанса с первыми
12... 1< «моторными» гармониками нормальной
силы К,
действующей т
соответствующий
участок коленчатого вала. Это условие
выполняется, если
a>oinin>(6...8)
—“i
где
п^..
— максимально возможная рабочая частота
вращения коленчатого вала двигателя.
Принципиально
добиться выполнения этого условия
можно увеличением нзгибной жесткости
вала в пролетах между соседними коренными
опорами и уменьшением подвижных масс
КШМ. Увеличению
изгибной жесткости кривошипа
способствуют:
применение
в конструкции двигателя полноопориых
коленчатых валов;
уменьшение
длины коренных и шатунных шеек ори
одновременном увеличении их диаметра.
